Opracowania dotyczące symetrii i parkietaży
Opracowania z tej grupy tematycznej należą do natępujących mniejszych działów.
1. Rozmaite rodzaje symetrycznych parkietaży płaszczyzny:
[P1]
"O kilku rodzajach regularnych parkietaży płaszczyzny"
autorstwa Patrycji Kumaszki (o parkietażach platońskich, archimedesowych i odbiciowych);
[P2]
"Parkietaże półobrotowe"
autorstwa Anny Zwęglińskiej;
[P3]
"Klasyfikacja parkietaży 2-Archimedesowych"
autorstwa Julii Bugiel;
[P4]
"Klasyfikacja ekwitranzytywnych parkietaży za pomocą wielokątów foremnych"
autorstwa Weroniki Buchar;
2. Matematyczna analiza różnych rodzajów parkietaży w stylu grafik M.C. Eschera:
[E1]
"Parkietaże typu Eschera na płaszczyźnie"
autorstwa Emilii Chmielewskiej;
[E2]
"O pewnej klasie regularnych parkietaży z dwoma rodzajami płytek"
autorstwa Diany Krawczyńskiej;
[E3]
"Klasyfikacja parkietaży izotoksalnych o niesymetrycznych krawędziach"
autorstwa Małgorzaty Moc.
[E4]
"Klasyfikacja zakresów kształtów płytek w wielokątowych parkietażach izohedralnych o
niesymetrycznych płytkach"
autorstwa Pawła Gielgiera.
[E5]
"Klasyfikacja zakresów kształtów płytek w parkietażach izohedralnych o czworokątnych i sześciokątnych
niesymetrycznych płytkach"
autorstwa Patrycji Pachuc.
3. Metoda orbifoldów Johna Conwaya i jej zastosowania:
[O1]
"O symetriach wzorów płaskich"
autorstwa Kaliny Kijewskiej;
[O2]
"Klasyfikacja szlaków ze względu na symetrie metodą Conwaya"
autorstwa Marii Kaczmarek;
[O3]
"Klasyfikacja parkietaży izohedralnych o niesymetrycznych płytkach"
autorstwa Katarzyny Siejek;
[O4]
"Klasyfikacja zakresów kształtów płytek w wielokątowych parkietażach izohedralnych o
niesymetrycznych płytkach"
autorstwa Pawła Gielgiera.
[O5]
"Klasyfikacja zakresów kształtów płytek w parkietażach izohedralnych o czworokątnych i sześciokątnych
niesymetrycznych płytkach"
autorstwa Patrycji Pachuc.
4. Parkietaże w przestrzeni, na sferze i na płaszczyźnie nieeuklidesowej:
[S1]
"Odbiciowe parkietaże przestrzeni o czworościennych klepkach"
autorstwa Pauliny Górskiej.
[S2]
"Odbiciowe parkietaże przestrzeni o klepkach
będących ostrosłupami"
autorstwa Darii Przybylak.
[S3]
"Parkietaże platońskie i szachownice archimedesowskie w geometrii
hiperbolicznej"
autorstwa Mateusza Suwary.
[S4]
"Parkietaże półobrotowe na sferze"
autorstwa Marcina Kędzierskiego.
Poniżej przytaczam obszerniejsze opisy poszczególnych pozycji z tej grupy tematycznej.
Dział 1:
Rozmaite rodzaje symetrycznych parkietaży płaszczyzny
Zamieszczone w tym dziale opracowania dotyczą różnych rodzajów symetrycznych parkietaży.
Prace [P1], [P3] i [P4] dotyczą różnych rodzajów parkietaży za pomocą wielokątów foremnych (niekoniecznie jednakowych).
Wśród nich są parkietaże FOREMNE zwane też PLATOŃSKIMI
(omówione w [P1]), parkietaże PÓŁFOREMNE zwane też ARCHIMEDESOWYMI
(opisane i sklasyfikowane również w [P1]),
a także tzw. parkietaże 2-ARCHIMEDESOWE (przeanalizowane w [P3]), i w końcu
tzw. parkietaże EKWITRANZYTYWNE (omówione i sklasyfikowane w [P4]).
W pracach [P1] i [P2] omówione są parkietaże o dowolnych wielokątnych płytkach mające specjalne własności symetrii zwane
ODBICIOWOŚCIĄ (omówione w [P1])
oraz PÓŁOBROTOWOŚCIĄ (omówione w [P2]).
|
|

przykłady parkietaży odbiciowych
|
[P1] Parkietaże foremne, półforemne i odbiciowe
Patrycja Kumaszka, "O kilku rodzajach regularnych parkietaży płaszczyzny", praca licencjacka, 2015.
plik pdf
W tej pracy znajdziecie opisy wszystkich parkietaży foremnych, półforemnych i odbiciowych,
wraz z uzasadnieniem, że innych takich parkietaży nie ma (będzie to więc tzw, KLASYFIKACJA parkietaży tych
trzech typów). Parkietaże foremne, to parkietaże za pomocą jednakowych wielokątów foremnych.
Parkietaże półforemne to parkietaże, których płytki są niejednakowymi wielokątami foremnymi, ale w których
płytki te są rozmieszczone w ten sam sposób wokół wszystkich wierzchołków parkietażu.
(Parkietaże półforemne są też nazywane parkietażami archimedesowymi). Wreszcie parkietaże odbiciowe
to takie parkietaże, w których każde dwie płytki sąsiadujące ze sobą przez krawędź są do siebie symetryczne
wględem tej wspólnej krawędzi.
Okazuje się, że są tylko 3 rodzaje parkietaży foremnych (platońskich), 8 rodzajów parkietaży półforemnych (archimedesowych),
i również 8 rodzajów parkietaży odbiciowych.

parkietaże foremne (platońskie)
|

przykłady parkietaży półforemnych (archimedesowych)
|
[P2] Parkietaże półobrotowe
Anna Zwęglińska, "Parkietaże półobrotowe", praca licencjacka, 2017.
plik pdf
Parkietaż półobrotowy to taki parkietaż wielokątami, w którym dowolne dwie płytki sąsiadujące przez krawędź
są do siebie półobrotowo symetryczne względem środka tej krawędzi. Znaczy to, że każda z tych płytek
jest obrazem drugiej w obrocie o kąt 180 stopni względem środka ich wspólnej krawędzi. W pracy znalezione zostają
wszystkie takie parkietaże, wraz z opisaniem wszystkich możliwych kształtó ich płytek. Okazuje się na przykład,
że płytki takich parkietaży mogą być tylko trójkątami, czworokątami lub sześciokątami. Okazuje się,
że płytką parkietażu półobrotowego może być dowolny trójkąt oraz dowolny czworokąt (także niewypukły!),
natomiast niedowolny sześciokąt. W pracy opisane są więc także wszyskie sześciokąty mogące być płytkami półobrotowych
parkietaży.
|
|

przykład parkietażu półobrotowego
|
[P3] Parkietaże 2-archimedesowe
Julia Bugiel, "Klasyfikacja parkietaży 2-Archimedesowych", praca magisterska, 2017.
plik pdf
Parkietaże 2-archimedesowe składają się z płytek będących niejednakowymi wielokątami foremnymi rozmieszczonymi
w taki sposób, że naokołom wierzchołków pojawiają się dokładnie dwie różne konfiguracje tych płytek. W pracy
znalezione zostały (czyli sklasyfikowane) wszystkie pary konfiguracji płytek wokół wierzchołków realizowane
w parkietażach 2-archimedesowych. Okazuje się, że jest 16 takich par konfiguracji.
W pracy jest też pokazane, że dla czterech spośród tych par konfiguracji
realizujące je parkietaże 2-archimedesowe są jednoznaczne, natomiast dla pozostałych dwunastu par liczba
istotnie różnych parkietaży 2-archimedesowych realizujących takie pary jest nieskończena.
W tej pracy korzysta się z przeprowadzonej w pracy [P1] klasyfikacji 21 konfiguracji wielokątów foremnych
szczelnie otaczających pojedynczy wierzchołek.
|
|

przykład parkietażu 2-archimedesowego
|
[P4] Parkietaże ekwitranzytywne o foremnych płytkach
Weronika Buchar, "Klasyfikacja ekwitranzytywnych parkietaży za pomocą wielokątów foremnych", praca magisterska, 2017.
plik pdf
Parkietaż nazywamy ekwitranzytywnym jeśli dla dowolnych dwóch płytek tego samego kształtu
istnieje symetria całego parkietażu przekształcająca jedną z tych płytek na drugą
(poglądowo znaczy to, że te płytki o tym samym kształcie są położone w taki sam sposób względem reszty parkietażu).
W pracy analizowane są parkietaże ekwitranzytywne, w których wszystkie płytki są wielokątami foremnymi.
Przekonujemy się, że istnieją dokładnie 22 takie parkietaże. Również w tej pracy korzysta się z przeprowadzonej w pracy [P1]
klasyfikacji 21 konfiguracji wielokątów foremnych
szczelnie otaczających pojedynczy wierzchołek.
|
|

przykład parkietażu ekwitranzytywnego
|
Dział 2:
Matematyczna analiza różnych rodzajów parkietaży w stylu grafik M.C. Eschera
Opracowania [E1], [E2] i [E3] dotyczą parkietaży, których płytki mogą mieć bardzo nieregularne kształty - nie muszą być
nawet wielokątami. Parkietaże tego rodzaju pojawiają się np. w twórczości holenderskiego grafika M.C. Eschera.
Opracowania zawierają matematyczne opisy i klasyfikacje
różnych typów takich parkietaży. Prace te mogą stanowić podstawę do projektowania własnych parkietażowych
kompozycji o takich typach symetrii, jakie nie pojawiły się w twórczości Eschera.
Praca [E1]
dotyczy parkietaży, w których wszystkie płytki mają ten sam kształt,
natomiast praca [E2]
analizuje parkietaże z płytkami o dwóch różnych kształtach.
W pracy [E3]
rozważającej jeszcze inny rodzaj symetrii
parkietaży, pojawiają się przykłady zarówno z jednym jak i z dwoma kształtami płytek.
Opracowanie [E4],
choć na pierwszy rzut oka nie ma związku z kompozycjami Eschera, w rzeczywistości także
stanowi źródło możliwych inspiracji do tworzenia tego typu kompozycji, przy czym w tym przypadku
wszystkie płytki mają ten sam kształt, zaś omówione tu typy parkietaży są różne od tych
omówionych w opracowaniu [E1].
|
|

tworzenie regularnego parkietażu
z nieregularnych wielokątów
|
[E1] Parkietaże regularne oparte na foremnym (platońskim) parkietażu kwadratami
Emilia Chmielewska,
"Parkietaże typu Eschera na płaszczyźnie", praca magisterska, 2002.
plik pdf
Holenderski grafik M.C. Escher stworzył liczne kompozycje, które nazywał "regularnymi podziałami płaszczyzny".
W tych kompozycjach płaszczyzna jest zapełniana w sposób szczelny, zgodnie z pewnymi precyzyjnymi regułami
przekształceń, jednakowymi nieregularnymi figurami, którym Escher nadaje formę ptaków, ryb, jaszczurek, aniołów,
łodzi żaglowych lub innych rozpoznawalnych obiektów. W prezentowanej pracy przeprowadzony został matematyczny opis,
oraz analiza i klasyfikacja, pewnej sporej rodziny parkietaży mających takie cechy jak wspomniane kompozycje Eschera.
Są to parkietaże, w których płytki rozmieszczone są w kombinatorycznie podobny sposób jak kwadratowe płytki
w parkietażu foremnym, ale reguły ich przekształcania na siebie mogą być rozmaite i skomplikowane.
|
|

jeden z 16 schematów symetrii dla siatki kwadratowej (po modyfikacji kształtu płytek)
|
|

regularny parkietaż M.C. Eschera
oparty na kwadratowej sieci
|
Okazuje się, że istnieje 16 koherentnych zestawów reguł przekształceń, którymi można się posługiwać przy
tworzeniu takich regularnych parkietaży. Dla każdej z tych reguł kształty płytek można modyfikować w dwóch
krokach. Najpierw, kwadraty można czasem zastąpić innymi czworokątami spełniającymi pewne warunki
(zależne od rozpatrywanego zestawu reguł przekształceń), i prezentowana praca zawiera kompletną analizę możliwości
takich czworokątnych kształtów dla wszystkich zestawów reguł. Następnie, w czworokątnym parkietażu można
dokonać w sposób systematyczny i regularny modyfikacji niektórych boków w płytkach, by stały się
krzywoliniowe. Ta ostatnia możliwość modyfikacji nie podlega już matematycznej analizie,
i jest raczej kwestią indywidualnej inwencji i pomysłowości. W pracy ukazane są przykłady takich modyfikacji.
Praca może być wykorzystana jako instrukcja tworzenia własnych kompozycji przypominających te
opracowywane przez Eschera, i realizujących wszystkie matematycznie możliwe zestawy reguł przekształceń.
[E2] Parkietaże 2-regularne naprzemienne (zainspirowane twórczością M.C. Escher'a)
Diana Krawczyńska,
"O pewnej klasie regularnych parkietaży z dwoma rodzajami płytek", praca magisterska, 2019.
plik pdf
Klasa parekietaży opisana w tej pracy zainspirowana została grafikami holenderskiego artysty M.C. Escher'a.
Parkietaż nazywamy regularnym jeśli dla każdych dwóch płytek istnieje symetria parkietażu przeprowadzająca
jedną z tych płytek na drugą. Kształty płytek nie muszą być przy tym regularne ani symetryczne, nie muszą też być wielokątami.
Parkietaż nazywamy 2-regularnym, jeśli składa się z dwóch rodzajów płytek,
i dla dowolnych dwóch płytek TEGO SAMEGO RODZAJU istnieje symetria parkietażu przeprowadzająca
jedną z tych płytek na drugą. Parkietaż 2-regularny nazywamy naprzemiennym, gdy płytki sąsiadujące ze sobą
przez krawędź są zawsze dwóch różnych rodzajów. Jest to własność ulubiona przez Eschera, gdyż pozwala
pomalować płytki dwoma kolorami w taki sposób, że płytki tego samego rodzaju mają ten sam kolor, zaś
płytki sąsiadujące przez krawędź mają różne kolory. W pracy znalezione zostały wszystkie typy takich parkietaży,
a jest ich jak się okazuje aż 37. Analiza grafik Eschera pokazuje, że artysta ten wykorzystał w swoich
kompozycjach jedynie 12 spośród wszystkich 37 typów takich parkietaży. Pozostałe typy czekają jeszcze na swoje
artystyczne realizacje.
|
|

przykład 2-regularnego naprzemiennego parkietażu M.C. Eschera
|
[E3] Parkietaże izotoksalne (o symetrii działającej przechodnio na krawędziach)
Małgorzata Moc,
"Klasyfikacja parkietaży izotoksalnych o niesymetrycznych krawędziach", praca magisterska, 2019.
plik pdf
Wśród parkietaży spotykamy rozmaite rodzaje symetrii. Może się np. zdarzyć, że wszystkie płytki parkietażu są
w taki sam sposób położone względem reszty parkietażu (tzw. parkietaże regularne, w których wszystkie płytki muszą mieć jednakowy kształt),
albo że jednakowe położenie
względem reszty parkietażu mają wszyskie jego wierzchołki (wtedy płytki mogą mieć różne kształty, a przykładami
są tu parkietaże półforemne, czyli archimedesowe). Jest też możliwe, że jednakowe położenie względem reszty
parkietażu mają jego wszystkie krawędzie. Parkietaże o takim mniej znanym rodzaju symetrii nazywają się
IZOTOKSALNYMI. Nietrudno się przekonać, że w takim parkietażu występuje albo jeden albo dwa rodzaje płytek.
W pracy analizowane są parkietaże izotoksalne o dodatkowej własności "niesymetryczności" krawędzi.
Ponieważ płytki w takich parkietażach mogą mieć zupełnie nieregularne kształty, i można te kształty modyfikować
jednocześnie we wszystkich płytkach bez zmiany istotnych cech parkietażu, w pracy opisane jest pojęcie TYPU KOMBINATORYCZNEGO
parkietażu izotoksalnego, odzwierciedlające własnie takie istotne cechy.
Znalezione są wszystkie typy kombinatoryczne izotoksalnych parkietaży o niesymetrycznych krawędziach,
i okazuje się, że jest ich 13
|
|

przykłady parkietaży izotoksalnych
|
[E4] Kształty płytek w wielokątowych parkietażach izohedralnych
Paweł Gielgier,
"Klasyfikacja zakresów kształtów płytek w wielokątowych parkietazach izohedralnych o
niesymetrycznych płytkach", praca magisterska, 2020.
plik pdf
Regularne parkietaże, będące jednym z ważnych motywów w twórczości M.C. Eschera,
zostały gruntownie zbadane przez matematyków. Sklasyfikowane zostały wszystkie możliwe
TYPY KOMBINATORYCZNE takich parkietaży (czyli reguły budownia takich parkietaży
z pojedynczej płytki pewnego rodzaju), i okazało się, że przy założeniu niesymetyryczności płytki
typów takich jest 46. Czytelnik może zapoznać się z pewnym nowym ujęciem
tej klasyfikacji, wg pomysłu błyskotliwego brytyjskiego matematyka Johna Conwaya, w opracowaniu
[O3] opisanym poniżej.
W tu opisywanym opracowaniu [E4], dla wybranej połowy spośród wspomnianych 46 typów,
znalezione są wszystkie możliwe wielokątne kształty płytek pozwalające budować parkietaż
analizowanego typu. Można to traktować jak instrukcję tworzenia ciekawych i nietypowych
regularnych parkietaży w stylu Eschera, przy czym wskazane wielokątowe kształty można
dalej modyfikować, zastępując w systematyczny sposób brzegowe proste segmenty w płytkach
zakrzywionymi liniami wg własnego pomysłu. Wybrane do analizy i omówione typy są inne niż te opisane
w pokrewnej pracy [E1].
|
|
|
[E5] Kształty płytek w wielokątowych parkietażach izohedralnych - część druga
Patrycja Pachuc,
"Klasyfikacja zakresów kształtów płytek w parkietazach izohedralnych o czworokątnych i sześciokątnych
niesymetrycznych płytkach", praca magisterska, 2025.
plik pdf
Omawiana tu praca [E5] jest kontynuacją poprzedniej pracy [E4].
Zamyka ona temat rozpoczęty w pracy [E4], czyli analizę wszystkich możliwych kaształtów płytek
dla wszystkich typów odpowiednio regul;arnych parklietaży (tzw. parkietaży izohedralnych).
Spośród wszystkich 46 typów takich parkietaży, w poprzedniej pracy [E4] omówione zostały 23 typy,
w tym wszystkie typy o płytkach trójkątnych i 5-kątnych, oraz kilka typów 4-kątowych.
W pracy [E5] analizowane są wszystkie typy o płytkach 6-kątnych, oraz wszytkie pozostałe typy
4-kątowe - łącznie kolejne 23 typy takich parkietaży. Dostajemy w ten sposób dalsze nieoczywiste
schematy tworzenia regularnych kompozycji w stylu Eschera, wyczerpując z matematycznego punktu widzenia
wszystkie potencjalne opcje takich schematów.
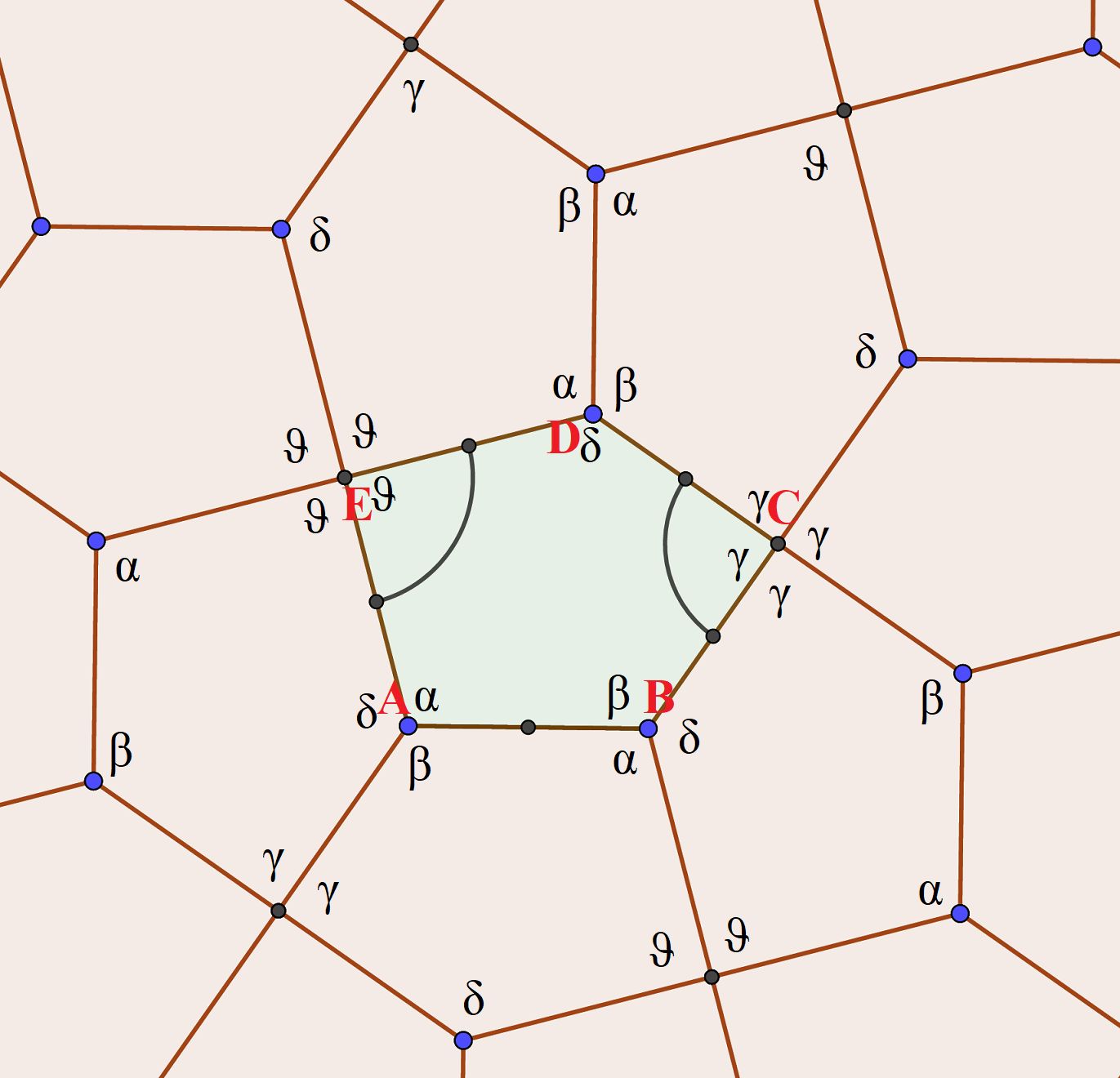
Rysunek obok przedstawia parkietaż izohedralny jednego z mniej oczywistych typów 4-kątowych,
ilustrując możliwość zastosowania w nim płytek o ciekawym niewypukłym kształcie.
|
|
|
Dział 3: Metoda orbifoldów Johna Conwaya i jej zastosowania
(zwłaszcza do klasyfikacji parkietaży izohedralnych)
Zmarły w roku 2020 (na choroby towarzyszące zakażeniu koronawirusem) John Conway to błyskotliwy brytyjski matematyk
o niezwykle oryginalnej osobowości i inwencji. Dokonał wielu spektakularnych odkryć, ale w gruncie rzeczy traktował
matematykę jako fascynującą zabawę. Dążył do wyrażenia trudnych zagadnień matematycznych w możliwie prosty
i atrakcyjny sposób. Interesował się grami i łamigłówkami, wymyślił grę w życie.
John Conway opracował nowy sposób przeprowadzenia dowodu, że istnieje dokładnie 17 typów symetrii wzorów płaskich.
Wykorzystał do tego nowoczesne i
niezbyt szeroko znane, ale bardzo poglądowe pojęcie orbifoldu. Prezentował ten dowód przy różnych okazjach,
a nawet zawarł jego szkicowy opis w jednej ze swoich książek. Znalazł też kilka dalszych zastosowań tej "metody orbifoldów"
do zagadnień dotyczących symetrycznych obiektów płaskich. Praca
[O1] zawiera przystępny i kompletny opis klasyfikacji
symetrii wzorów płaskich metodą Conwaya. Praca [O2]
zawiera klasyfikację typów symetrii wzorów zwanych szlakami, metodą orbifoldów, zgodnie z pomysłem Conwaya.
W pracy [O3] przedstawiona jest klasyfikacja za
pomocą orbifoldów, także według pomysłu Conwaya, tzw. izohedralnych parkietaży o niesymetrycznych płytkach.
Praca [O4] jest uzupełnieniem pracy [O3] - analizowane są
w niej możliwe kształty płytek w poszczególnych "typach" izohedralnych parkietaży; ta ostatnia praca nie odwołuje się już
do orbifoldów ani do innych idei Conwaya.

 wzór płaski, środki jego obrotowych symetrii, dziedzina fundamentalna grupy symetrii, i orbifold
wzór płaski, środki jego obrotowych symetrii, dziedzina fundamentalna grupy symetrii, i orbifold
[O1] Mozaiki, czyli regularne wzory płaskie, i ich 17 typów symetrii
Kalina Kijewska,
"O symetriach wzorów płaskich", praca magisterska, 2014.
plik pdf
Typy symetrii płaskich regularnych wzorów (powtarzalnych w dwóch różnych kierunkach) zostały zbadane i opisane
pod koniec XIX wieku. Okazało się, że jest 17 typów takich wzorów, jeśli brać pod uwagę tylko istotne cechy ich
symetrii. Pod koniec XX wieku John Conway zaproponował zupełnie nowy i koncepcyjnie bardzo piękny dowód tego faktu.
Choć dający się opowiedzieć w sposób przystępny, dowód ten nie doczekał się kompletnego opisu w prostym języku.
Praca [O1] jest próbą takiego właśnie opisu, i wydaje się dostępna nawet jako materiał dla interesujących się
matematyką uczniów szkoły średniej.
Orbifold wzoru płaskiego to pewna powierzchnia, z oznaczonymi punktami specjalnymi, która koduje "sposób
w jaki wzór jest symetryczny". Mówiąc nieco bardziej zaawansowanym językiem, orbifold to przestrzeń orbit
grupy symetrii wzoru. Orbifoldowa klasyfikacja typów symetrii wzorów płaskich wykorzystuje znajomość klasyfikacji
powierzchni, i jest to najbardziej zaawansowane matematyczne narzędzie wykorzystywane przy tej klasyfikacji.
Klasyfikacja powierzchni jest przytoczona w sposób przystępny w tej pracy.
Dodatkowym wykorzystywanym narzędziem jest, także przytoczone i omówione w pracy, pojęcie charakterystyki Eulera powierzchni.
|
|
 analiza symetrii pewnego wzoru - kolory ukazują 2 rodzaje symetrii z poślizgiem
analiza symetrii pewnego wzoru - kolory ukazują 2 rodzaje symetrii z poślizgiem
|
[O2] Szlaki i ich typy symetrii - sklasyfikowane metodą orbifoldów Conwaya
Maria Kaczmarek,
"Klasyfikacja szlaków ze względu na symetrie metodą Conwaya", praca magisterska, 2016.
plik pdf
Tak jak w powyżej opisanej pracy [O1] orbifoldy są wykorzystywane do znalezienia wszystkich
typów symetrii wzorów rozciągniętych na całej płaszczyźnie, tak w tej pracy ta sama metoda
zastosowana jest do tzw. szlaków, czyli rytmicznych wzorów rozciągających się
w jednym kierunku. Okazuje się, że takich typów symetrii dla szlaków jest dokładnie siedem.

[O3] Parkietaże regularne, ich typy izohedralne, i klasyfikacja tych typów metodą Conwaya
Katarzyna Siejek,
"Klasyfikacja parkietaży izohedralnych o niesymetrycznych płytkach", praca magisterska, 2018.
plik pdf
Ta praca, nagrodzona w ogólnopolskim konkursie mBanku na najlepszą pracę dyplomową z matematyki,
dotyczy klasyfikacji typów parkietaży izohedralnych. Parkietaże izohedralne, zwane też regularnymi,
to parkietaże o płytkach jednego kształtu spełniające warunek regularności mówiący, że wszystkie płytki
są identycznie położone względem reszty parkietażu. Matematycznie wyraża się tą własność przez
wymaganie, by dla dowolnych dwóch płytek istniała symetria całego parkietażu przeprowadzająca
jedną z tych płytek na drugą. Przykłady parkietaży izohedralnych z płytkami o nieregularnych kształtach
zamieszczone są na rysunkach powyżej, przy omówieniach opracowań [E1], [E3] i [E4]. Parkietaże
izohedralne różniące się od siebie kształtem mogą mieć tą samą zasadę budowy. Mówimy wtedy, że parkietaże te
mają ten sam typ. Jak dokładnie określa się taki typ, można dowiedzieć się z pracy.
|
W pracy znalezione są wszystkie typy parkietaży izohedralnych, metodą zaproponowaną przez Johna Conwaya,
wykorzystującą pojęcie orbifoldu dla grupy symetrii parkietażu. O orbifoldach jest mowa we wspomnianej
powyżej pracy [O1], ale i w tej pracy są one
wyczerpująco przypomniane, opisane i omówione. Dużą rolę w pracy odgrywa też analiza powierzchni i tego
co z nimi się dzieje pod wpływem rozcinania wzdłuż pewnych krzywych. Teoria powierzchni, ich klasyfikacja,
a także pojęcie charakterystyki Eulera powierzchni, są przystępnie wprowadzone w tym zakresie,
w jakim są potrzebne do przeprowadzania rozumowań i analiz dotyczących parkietaży izohedralnych.
|
|
 klasyfikowanie regularnych parkietaży o zadanej symetrii sprowadza się do klasyfikowania
klasyfikowanie regularnych parkietaży o zadanej symetrii sprowadza się do klasyfikowania
"śladów" zostawionych przez te parkietaże na powierzchni orbifoldu;
po rozcieciu powierzchni orbifoldu wzdłuż takiego "śladu" otrzymuję się płytkę parkietażu
|
[O4] Kształty płytek w wielokątowych parkietażach izohedralnych
Paweł Gielgier,
"Klasyfikacja zakresów kształtów płytek w wielokątowych parkietazach izohedralnych o
niesymetrycznych płytkach", praca magisterska, 2020.
plik pdf
|
Na rusynku obok można zobaczyć, że kształt płytki parkietażu izohedralnego, nawet gdy jest to kaształt wielokąta,
może być całkiem niebanalny. Zamieszczona tu praca zawiera analizę wszystkich możliwych wielokątowych kształtów płytek
dla poszczególnych rodzajów (typów) parkietaży izohedralnych. W istocie jest tu przeanalizowana w pełni
połowa spośród aż 46 typów takich parkietaży. Pracę można traktować jako uzupełnienie poprzedniej
pracy [O3]. Można ją też czytać jak instrukcje tworzenia intersujących parkietaży, dostarczającą wielokątowe
schematy, które można poddawać dalszym twórczym przeróbkom we własnym zakresie.
|
|
 niebanalny dobór kształtu płytki dla jednego z typów izohedralnych parkietaży
niebanalny dobór kształtu płytki dla jednego z typów izohedralnych parkietaży
|
[O5] Kształty płytek w wielokątowych parkietażach izohedralnych - ciąg dalszy i ostateczne skompletowanie informacji
|
Patrycja Pachuc,
"Klasyfikacja zakresów kształtów płytek w parkietażach izohedralnych o sześciokątnych i czworokątnych
niesymetrycznych płytkach",
praca magisterska, 2025.
plik pdf
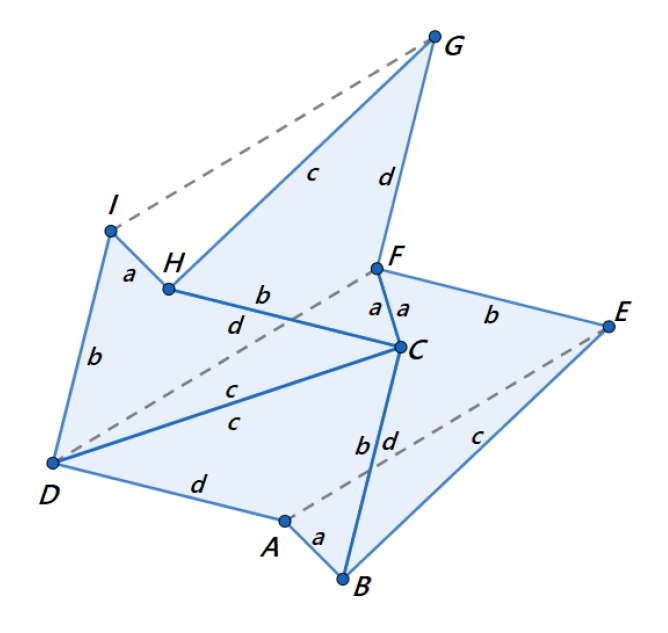
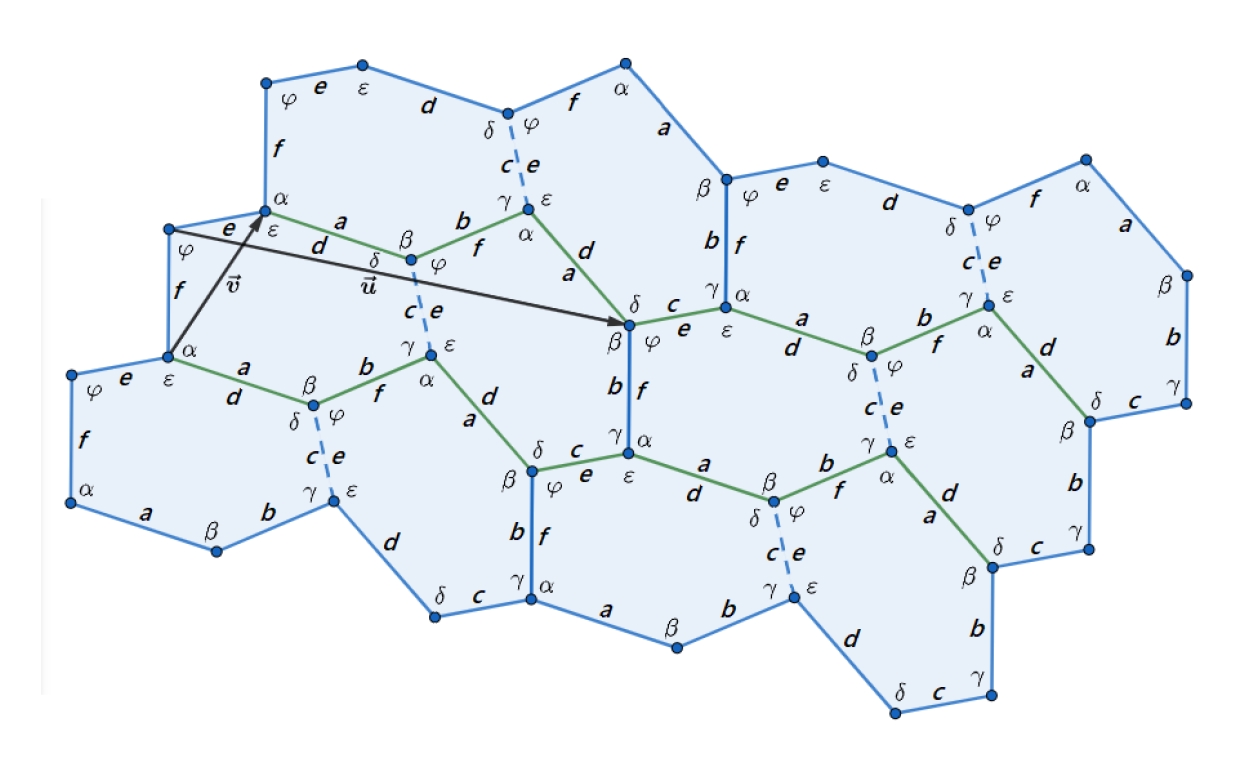
Rysunek obok przedstawia jeszcze inny wariant parkietażu izohedralnego, tym razem z płytkami
o kształcie dość nieregularnego sześciokąta. Pochodzi on z zamieszczonej tu pracy [O5],
w której przeanalizowana została (pod kątem możliwych kaształtów płytek) druga połowa spośród 46 typów
parkietaży izohedralnych. Również tą pracę można potraktować jako inspirację do tworzenia
niebanalnych regularnych kompozycji, poprzez twórczą modyfikację wielokątowych kształtów płytek
zmieniającą ich krawędzie w odpowiednio zaprojektowane zakrzywione linie.
|
|
|
Dział 4: Symetryczne parkietaże w przestrzeni, na sferze i na płaszczyźnie nieeuklidesowej
[S1] Odbiciowe parkietaże przestrzeni za pomocą jednakowych płytek w kształcie czworościanów
i odbiciowe parkietaże sfery za pomocą trójkątów sferycznych
Paulina Górska,
"Odbiciowe parkietaże przestrzeni o czworościennych klepkach", praca magisterska, 2020.
plik pdf
Parkietaż przestrzeni to zapełnienie całej przestrzeni bryłami bez pozostawienia żadnych wolnych miejsc
(te bryły są wtedy nazywane płytkami lub klepkami takiego parkietażu).
Parkietaż przestrzeni jest ODBICIOWY jeśli jego płytki są wielościanami, i jeśli każde dwie płytki
sąsiadujące ze sobą przez ścianę są dla siebie lustrzanie symetryczne względem tej wspólnej ściany.
Najprostszym przykładem takiego odbiciowego parkietażu jest podział przestrzeni na jednakowe sześciany (kostki).
Nietrudno też od razu zauważyć, że wszystkie płytki dowolnego odbiciowego parkietażu muszą mieć ten sam kształt.
W pracy znalezione są i opisane (czyli sklasyfikowane) wszystkie odbiciowe parkietaże przestrzeni, których
płytki mają kształt czworościanu. Okazuje się, że są tylko cztery takie parkietaże - tylko cztery kształty czworościanu
nadają się do zapełnienia przestrzeni w sposób odbiciowy.
Pomocniczym zagadnieniem przeanalizowanym w tej pracy (i stosowanym później do głównego zagadnienia) są odbiciowe
parkietaże powierzchni sfery za pomocą płytek będących tzw, trójkątami sferycznymi. W pracy znalezione zostały
wszystkie takie sferyczne parkietaże, a jest ich łącznie 10, i dodatkowo jedna nieskończona seria parkietaży
powstających przez podział sfery równikiem i kilkoma południkami (przypominająca obieranie pomarańczy).
|
|

odbiciowy parkietaż sfery o trójkątnych klepkach
|
 czworościenne płytki odbiciowych parkietaży przestrzeni - pełna lista
czworościenne płytki odbiciowych parkietaży przestrzeni - pełna lista
[S2] Odbiciowe parkietaże przestrzeni wielościennymi płytkami o kształcie ostrosłupów
Daria Przybylak,
"Odbiciowe parkietaże przestrzeni o płytkach będących ostrosłupami",
praca magisterska, 2021.
plik pdf
Ta praca jest kontynuacją pracy [S1]. Dotyczy ona nadal odbiciowych parkietaży przestrzeni,
czyli takich zapełnień przestrzeni jednakowymi wielościanami, że każde dwa wielościany mające wspólną ścianę
są do siebie symetryczne względem płaszczyzny zawierającej tą ścianę.
W poprzedniej pracy [S1] znalezione zostały
wszystkie takie odbiciowe parkietaże o płytkach czworościennych. W tej pracy autorka idzie o krok dalej,
i znajduje wszystkie parkietaże odbiciowe o płytkach "ostrosłupowych". Oczywiście czworościany to szczególny
przypadek ostrosłupów, więc rzecz idzie w istocie o parkietaże z płytkami w kształcie ostrosłupów
n-kątnych dla n>3. Ponieważ ostrosłupy różne od czworościanów
posiadają wierzchołek o kącie n-ściennym dla n>3, trudność polega na konieczności
przeanalizowania dopuszczalnych kształtów takich n-ściennych kątów bryłowych (które nie występowały
w czworościanach). To prowadzi autorkę do analizy i pomocniczej klasyfikacji odbiciowych parkietaży sfery za pomocą wielokątów różnych
od trójkątów. Dalsza analiza pozwala znaleźć wszystkie poszukiwane parkietaże ostrosłupami,
i okazuję się są tylko 3 takie parkietaże, a ich płytki to ostrosłupy czworokątne o trzech różnych kształtach.
W szczególności, okazuje się że żaden ostrosłup n-kątny z n większym niż 4 nie może być płytką
odbiciowego parkietażu przestrzeni.
|
|

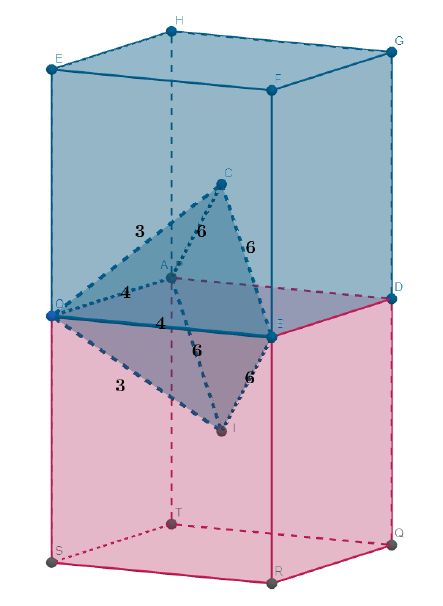
rysunki powyżej reprezentują
etapy opisanej w pracy konstrukcji najciekawszego odbiciowego parkietażu przestrzeni o płytkach
będących jednakowymi ostrosłupami czworokątnymi (płytka jest ukazana na rysunku po prawej)
|
[S3] Parkietaże platońskie (foremne) oraz szachownicowe parkietaże archimedesowe (półforemne) płaszczyzny nieeuklidesowej
Mateusz Suwara,
"Parkietaże platońskie i szachownice archimedesowskie w geometrii
hiperbolicznej", praca magisterska, 2012.
plik pdf
Na płaszczyźnie nieeuklidesowej niemożliwe jest skalowanie figur bez zmiany ich kształtu.
Ma to różne konsekwencje, ale jedna z nich dotyczy parkietaży. Nie ma na płaszczyźnie nieuklidesowej
problemu ze zdefiniowaniem analogonów pojęć parkietaży platońskich i archimedesowych, czyli specjalnych
parkietaży których wszystkie klepki są (nieeuklidesowymi) wielokątami foremnymi. Co więcej, takich
parkietaży jest na płaszczyźnie nieeuklidesowej dużo więcej niż w zwsykłej geometrii.
Jednak rozmiar wielokątów wchodzących w skłąd takich parkietaży jest jednoznacznie zdeterminowany
przez rodzaj parkietażu (nie jest możliwe przeskalowanie całego parkietażu). Praca zawiera omówienie
wspomnianych powyżej pojęć i zjawisk, a także wyliczenia długości boków i miar kątów w wielokątach
foremnych będących klepkami poszczególnych parkietaży.
|
|

dwa spośród nieskończenie wielu
parkietaży archimedesowych na płaszczyźnie nieeuklidesowej
(przedstawione w modelu dyskowym Poincare'go)
|
[S4] Parkietaże sfery za pomocą jednakowych wielokątów sferycznych zgodnie z regułą półobrotowej
symetrii dla każdej pary przyległych płytek
Marcin Kędzierski,
"Parkietaże półobrotowe na sferze", praca magisterska, 2024.
plik pdf
Powierzchnia sfery stanowi uniwersum, w którym mamy do czynienia z konkurencyjną do euklidesowej
geometrią - tzw. geometrią sferyczną. W tej geometrii istnieją figury zwane wielokątami sferycznymi,
a z tych figur można tworzyć konstelancje pokrywające całą powierzchgnię sfery, zwane parkietażami
sferycznymi. Tak samo jak na zwykłej płaszczyźnie (euklidesowej), również na sferze parkietaże mogą być
mniej lub bardziej regularne. Mamy więc np. parkietaże platońskie (za pomocą jednakowych sferycznych
wielokątów foremnych). Mamy parkietaże odbiciowe, w których każde dwie płytki mające wspólny bok
są swoimi lustrzanymi obrazami w symetrii względem tego współnego boku (i takie parkietaże sfery zostały
w pełni opisane w wyżej wspomnianych pracach [S1] i [S2]). W tu omawianej pracy [S4] znajduje się
pełen opis wszystkich możliwych parkietaży sferycznych zgodnych z inną regułą regularności,
mianowicie tzw. parkietaży sferycznych ODBICIOWYCH. Reguła "odbiciowości" polega na tym, że
każde dwie płytki posiadające wspólny bok są swoimi obrazami przez półobrót (czyli obrót o 180 stopni)
względem środka tego wspólnego boku.
Warto wspomnieć, że analogiczne parkietaże półobrotowe na zwykłej płaszczyźnie (euklidesowej)
opisane zostały w bardzo przystępny sposób np. zamieszczonej w tym zbiorze opracowań pracy
[P2].
Tu omawiana praca [S4] jest także bardzo przystępna. Między innymi, na początku zapoznaje czytelnika
z mnóstwem podstawowych pojęć i obiektów z geometrii sferycznej.
Wszystkie analizy, argumenty i konstrukcje w pracy poparte są licznymi pomocnymi rysunkami.
|
|
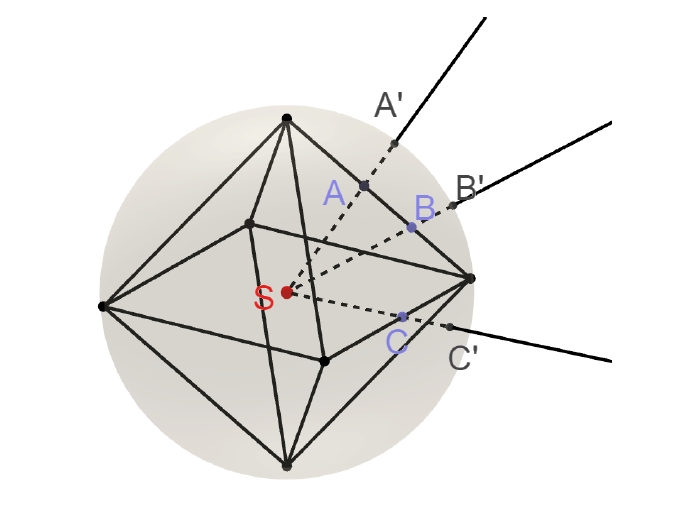
Rysynek ilustrujący pojęcie "rzutu promienistego" wielościanu
na opisaną na nim sferę, w wyniku czego na sferze powstaje parkietaż.
Jest to jedna z konstrukcji wykorzystanych w analizach z omawianej tu pracy [S4].
|

























