


Next: 4. Rachunek zbiorów
Up: Wstęp do matematyki
Previous: 2. Formuły równoważne
Zbiór (inaczej zwany mnogością) to podstawowe pojęcie w
matematyce. Przy jego pomocy można zdefiniować na gruncie teorii
mnogości (zwanej też teorią zbiorów) wszystkie inne
pojęcia matematyczne. Przyjmuje się, że jest to pojęcie pierwotne,
tzn. nie wymagające definicji. Z drugiej strony matematycy w praktyce nadają
temu pojęciu pewien określony intuicyjny sens. Intuicyjnie można
powiedzieć, że zbiór jest to objęcie przez umysł pewnej liczby
przedmiotów (materialnych lub duchowych), zwanych elementami tego
zbioru. Tę nieformalną definicję podajemy dla wygody czytelnika,
zastrzegając się jednak, że nie oddaje ona w pełni treści
pojęcia zbioru. Jest tylko pewnym przybliżeniem.
Zazwyczaj zbiory oznaczamy dużymi literami, zaś ich elementy
małymi literami. Gdy  jest elementem zbioru
jest elementem zbioru  , mówimy też, że
, mówimy też, że
 należy do
należy do  i zapisujemy to zdanie symbolicznie w postaci:
i zapisujemy to zdanie symbolicznie w postaci:
 nazywamy symbolem należenia do zbioru.
nazywamy symbolem należenia do zbioru.
oznacza zdanie  . Koniunkcję zdań postaci
. Koniunkcję zdań postaci
zapisujemy krócej w formie
Przykłady zbiorów to zbiór uczniów w klasie, zbiór jabłek na
drzewie, zbiór liczb rzeczywistych dodatnich. Przyjmujemy, że dwa
zbiory, które mają te same elementy, są równe. Innymi słowy, dla
dowolnych zbiorów  mamy
mamy
Zasadniczo zbiory
możemy określać na dwa sposoby.
Sposób 1. Określenie zbioru przez wypisanie jego elementów. Na
przykład, zapis
oznacza, że wszystkimi elementami zbioru  są Piotr, Jan, Ewa,
Ala,
są Piotr, Jan, Ewa,
Ala,  . W szczególności prawdą jest, że Piotr
. W szczególności prawdą jest, że Piotr  .
Podobnie zapis
.
Podobnie zapis
oznacza zbiór, którego wszystkie elementy to liczby
 .
.  oznacza zbiór, którego jedynym elementem jest
liczba
oznacza zbiór, którego jedynym elementem jest
liczba  . Należy tu podkreślić, że
. Należy tu podkreślić, że  i
i  to różne
obiekty. Podobnie jabłko i zbiór jednoelementowy złożony z jabłka
to dwa różne przedmioty. Najprościej wyjaśnić to mówiąc, że
jabłko wisi na drzewie, a zbiór złożony z tego jabłka istnieje w
umyśle.
to różne
obiekty. Podobnie jabłko i zbiór jednoelementowy złożony z jabłka
to dwa różne przedmioty. Najprościej wyjaśnić to mówiąc, że
jabłko wisi na drzewie, a zbiór złożony z tego jabłka istnieje w
umyśle.
W przypadku zbioru skończonego
dla wszystkich  prawdziwa jest równoważność
prawdziwa jest równoważność
Dlatego zapisy  i
i  oznaczają ten sam zbiór
złożony z
oznaczają ten sam zbiór
złożony z  .
.
Zanim przystąpimy do podania drugiego sposobu określania zbiorów,
wprowadzimy pojęcie funkcji zdaniowej.
Wypełniając różne formularze często wpisujemy różne słowa w
odpowiednie wolne miejsca. Rozważmy na przykład wyrażenie:
Gdy w miejsce kropek wpiszemy określenie jakiejś osoby (np. słowo
Janek), wyrażenie to stanie się zdaniem. Podobnie, jeśli w
wyrażeniu algebraicznym
w miejsce niewiadomej  wpiszemy konkretną liczbę, stanie sie ono
zdaniem.
Obydwa rozważane powyżej wyrażenia są przykładami funkcji
zdaniowych.
wpiszemy konkretną liczbę, stanie sie ono
zdaniem.
Obydwa rozważane powyżej wyrażenia są przykładami funkcji
zdaniowych.
Definicja 3.1
Wyrażenie

, które staje się zdaniem, gdy za

podstawimy obiekt określonego typu (np. element jakiegoś zbioru)
nazywamy funkcją zdaniową (predykatem). Jeśli określony
jest zbiór

, z którego bierzemy obiekty do podstawiania za
zmienną

, to mówimy, że zmienna

w funkcji zdaniowej

ma
zakres zmienności (lub krótko: zakres)

. Piszemy wówczas

. Można również rozważać funkcje zdaniowe bez
określania zakresu zmiennej.
W funkcji zdaniowej  zakresem zmiennej jest zbiór ludzi. W
zakresem zmiennej jest zbiór ludzi. W
 zakresem zmiennej
zakresem zmiennej  jest zbiór liczb rzeczywistych. Podobnie
definiuje się funkcje zdaniowe
jest zbiór liczb rzeczywistych. Podobnie
definiuje się funkcje zdaniowe
 większej
(skończonej) liczby zmiennych.
większej
(skończonej) liczby zmiennych.
Przykładem funkcji zdaniowej dwóch zmiennych jest wyrażenie  . Równania i nierówności (na przykład takie, jak rozważane w
rozdziale 2) to również funkcje zdaniowe.
. Równania i nierówności (na przykład takie, jak rozważane w
rozdziale 2) to również funkcje zdaniowe.
Przy pomocy spójników logicznych
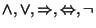 i nawiasów możemy z danych funkcji
zdaniowych tworzyć nowe (złożone) funkcje zdaniowe. Na przykład,
jeśli
i nawiasów możemy z danych funkcji
zdaniowych tworzyć nowe (złożone) funkcje zdaniowe. Na przykład,
jeśli  i
i  to dane funkcje zdaniowe, to również
to dane funkcje zdaniowe, to również
są funkcjami zdaniowymi, przy czym wymagamy tu zgodności zakresów
wspólnych zmiennych w tych funkcjach (o ile są określone); w naszym
przypadku zmienna  powinna mieć ten sam zakres w funkcjach
powinna mieć ten sam zakres w funkcjach  i
i
 .
Bardziej konkretny przykład to funkcja zdaniowa
.
Bardziej konkretny przykład to funkcja zdaniowa
(tu  oznacza zbiór liczb rzeczywistych).
Ogólnie, gdy
oznacza zbiór liczb rzeczywistych).
Ogólnie, gdy  jest formułą zdaniową, zaś
jest formułą zdaniową, zaś  są
funkcjami zdaniowymi o odpowiednio zgodnych zakresach zmiennych, to
podstawiając w
są
funkcjami zdaniowymi o odpowiednio zgodnych zakresach zmiennych, to
podstawiając w  funkcje
funkcje  za zmienne zdaniowe
za zmienne zdaniowe
 odpowiednio, dostajemy złożoną funkcję zdaniową.
odpowiednio, dostajemy złożoną funkcję zdaniową.
Teraz możemy przedstawić drugi sposób określania zbioru.
Sposób 2. Określenie zbioru przez podanie własności, którą mają
wszystkie jego elementy. Załóżmy, że  jest funkcją
zdaniową. Zapis
jest funkcją
zdaniową. Zapis
oznacza zbiór tych wszystkich  , dla których zdanie
, dla których zdanie  jest
prawdziwe3.1. Zauważmy, że wówczas dla wszystkich
jest
prawdziwe3.1. Zauważmy, że wówczas dla wszystkich  mamy
mamy
Jeśli zakresem zmiennej  w
w  jest dany
zbiór
jest dany
zbiór  , to zbiór
, to zbiór  istnieje, zapisujemy go wówczas
również w formie
istnieje, zapisujemy go wówczas
również w formie
 . Zapis ten odczytujemy następująco:
. Zapis ten odczytujemy następująco:
``zbiór takich  należących do
należących do  , które spełniają
warunek
, które spełniają
warunek  ''.
''.
W matematyce zbiory określone w ten sposób to
m.in.
 jest liczbą naturalną
jest liczbą naturalną (zbiór wszystkich liczb
naturalnych),
(zbiór wszystkich liczb
naturalnych),
 jest liczbą rzeczywistą
jest liczbą rzeczywistą (zbiór wszystkich
liczb rzeczywistych),
(zbiór wszystkich
liczb rzeczywistych),
zbiory liczb całkowitych  , liczb wymiernych
, liczb wymiernych  czy
liczb niewymiernych
czy
liczb niewymiernych  .
.
Szczególnym zbiorem jest tak zwany zbiór pusty, tzn. zbiór bez
elementów. Przyjęliśmy, że zbiory o tych samych elementach są
równe. Dlatego dowolne dwa zbiory puste są sobie równe. Istnieje
więc tylko jeden zbiór pusty. Oznaczamy go symbolem
 .
.
Rozważmy funkcję zdaniową
 . Wówczas
. Wówczas
oznacza zbiór takich liczb rzeczywistych  , które spełniają
warunek
, które spełniają
warunek  . Rozwiązując odpowiednie równanie znajdujemy, że
dla wszystkich liczb rzeczywistych
. Rozwiązując odpowiednie równanie znajdujemy, że
dla wszystkich liczb rzeczywistych  mamy
mamy
a zatem jedynymi elementami tego zbioru są liczby
 . Mamy więc
. Mamy więc
Lewa strona tej równości określa nasz zbiór przez podanie
warunku spełnianego przez jego elementy, prawa strona określa ten
sam zbiór przez wypisanie jego elementów.
Przykład. Antynomia (paradoks) Russella. Niech  oznacza
funkcję zdaniową
oznacza
funkcję zdaniową  . Wówczas nie istnieje zbiór
. Wówczas nie istnieje zbiór
 .
.
Dowód.
Przypuśćmy nie wprost, że zbiór
 istnieje. Wówczas
dla wszystkich
istnieje. Wówczas
dla wszystkich  mamy
mamy
W szczególności zdanie  jest słuszne, gdy
jest słuszne, gdy  oznacza
zbiór
oznacza
zbiór  . Wówczas dostajemy, że
. Wówczas dostajemy, że  wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
 , sprzeczność.
, sprzeczność. 



Next: 4. Rachunek zbiorów
Up: Wstęp do matematyki
Previous: 2. Formuły równoważne
Ludomir Newelski
2005-09-22
![]() jest elementem zbioru
jest elementem zbioru ![]() , mówimy też, że
, mówimy też, że
![]() należy do
należy do ![]() i zapisujemy to zdanie symbolicznie w postaci:
i zapisujemy to zdanie symbolicznie w postaci:
![]() mamy
mamy
![]() . Równania i nierówności (na przykład takie, jak rozważane w
rozdziale 2) to również funkcje zdaniowe.
. Równania i nierówności (na przykład takie, jak rozważane w
rozdziale 2) to również funkcje zdaniowe.
![]() i nawiasów możemy z danych funkcji
zdaniowych tworzyć nowe (złożone) funkcje zdaniowe. Na przykład,
jeśli
i nawiasów możemy z danych funkcji
zdaniowych tworzyć nowe (złożone) funkcje zdaniowe. Na przykład,
jeśli ![]() i
i ![]() to dane funkcje zdaniowe, to również
to dane funkcje zdaniowe, to również
![]() jest funkcją
zdaniową. Zapis
jest funkcją
zdaniową. Zapis
należących do
, które spełniają warunek
''.
![]() jest liczbą naturalną
jest liczbą naturalną![]() (zbiór wszystkich liczb
naturalnych),
(zbiór wszystkich liczb
naturalnych),
![]() jest liczbą rzeczywistą
jest liczbą rzeczywistą![]() (zbiór wszystkich
liczb rzeczywistych),
(zbiór wszystkich
liczb rzeczywistych),
![]() , liczb wymiernych
, liczb wymiernych ![]() czy
liczb niewymiernych
czy
liczb niewymiernych ![]() .
.
![]() .
.
![]() . Wówczas
. Wówczas

![]() oznacza
funkcję zdaniową
oznacza
funkcję zdaniową ![]() . Wówczas nie istnieje zbiór
. Wówczas nie istnieje zbiór
![]() .
.
![]() istnieje. Wówczas
dla wszystkich
istnieje. Wówczas
dla wszystkich ![]() mamy
mamy