14. Macierze symetryczne i funkcjonały kwadratowe

W tym rozdziale udowodnimy, że każda macierz symetryczna o wyrazach rzeczywistych jest diagonalizowalna. Następnie użyjemy tego faktu do opisu funkcjonałów kwadratowych na przestrzeni liniowej skończonego wymiaru.

Zakładamy tu, że $(V,\langle\cdot,\cdot\rangle)$ jest przestrzenią euklidesową wymiaru $n$ oraz ${\cal B}=\{b_1,\dots,b_n\}$ jest bazą ortonormalną $V$. By udowodnić, że każda macierz symetryczna jest diagonalizowalna, wygodnie jest wprowadzić pojęcie symetrycznego przekształcenia liniowego $F:V\rightarrow V$.

Definicja 14.1   Przekształcenie liniowe $F:V\rightarrow V$ jest symetryczne $\iff\langle F(v),w\rangle=\langle v,F(w)\rangle$ dla wszystkich $v,w\in V$.

Uwaga 14.2   $F$ jest symetryczne $\iff m_{{\cal B}}(F)$ jest symetryczna.

Dowód. Niech $A=m_{{\cal B}}(F)$.

$\Rightarrow.$ $A=[a_{ij}]_{n\times n}$, gdzie $a_{ij}=\langle b_i,F(b_j)\rangle$ (por. dyskusja po uwadze 10.8). $F$ jest symetryczne, więc

$$a_{ij}=\langle b_i,F(b_j)\rangle=\langle b_j,F(b_i)\rangle=a_{ji},$$

czyli macierz $A$ jest symetryczna.

$\Leftarrow.$ Załóżmy, że macierz $A$ jest symetryczna, tzn. $A=A^*$. Pokażemy, że $\langle F(v),w\rangle=\langle v,F(w)\rangle$ dla wszystkich $v,w\in V$. Standardowy iloczyn skalarny w przestrzeni $E^n$ możemy traktować jako iloczyn macierzy : $\langle X,Y\rangle= X^*\cdot Y$. Dlatego, korzystając z uwagi 11.2 i z tego, że $A=A^*$, mamy

$$\langle F(v),w\rangle=\langle [F(v)]_{{\cal B}},[w]_{{\cal B}... ... B}}=\left( A\cdot [v]_{{\cal B}}\right)^*\cdot [w]_{{\cal B}}=$$

$$[v]_{{\cal B}}^*\cdot A^*\cdot [w]_{{\cal B}}=[v]_{{\cal B}}^... ... [v]_{{\cal B}},[F(w)]_{{\cal B}}\rangle=\langle v,F(w)\rangle.$$

W kolejnym lemacie udowodnimy, że każda macierz symetryczna ma wartość własną. Najpierw sprawdzimy to dla macierzy wymiaru $2\times 2$.

Uwaga 14.3   Macierz symetryczna $A=\left[\begin{array}{cc}a&b\\ b&c\end{array}\right]$ ma wartość własną.

Dowód. $\varphi_A(X)=(a-X)(c-X)-b^2=X^2-(a+c)X+(ac-b^2)$. Wielomian ten ma pierwiastek rzeczywisty, bo

$$\Delta=(a+c)^2-4(ac-b^2)=(a^2+c^2-2ac)+4b^2=(a-c)^2+4b^2\geq 0.$$

Lemat 14.4   Macierz symetryczna ma wartość własną.

Dowód. Niech $A$ będzie macierzą symetryczną wymiaru $n\times n$ i niech $F_A:E^n\rightarrow E^n$ będzie przekształceniem liniowym o macierzy $A$. Z uwagi 14.2 wynika, że $F_A$ jest symetryczne. Na mocy lematu 12.2 istnieje $F_A$-niezmiennicza podprzestrzeń $W\subset {\mathbb{R}}^n$ wymiaru $1$ lub $2$.

Jeśli $dim(W)=1$, to dowolny niezerowy wektor $v\in W$ spełnia $F_A(v)=\lambda v$ dla pewnego $\lambda\in R$. $\lambda$ jest więc wartością własną przekształcenia $F_A$ i macierzy $A$.

Załóżmy więc, że $\dim(W)=2$. Niech $F':W\rightarrow W$ będzie obcięciem $F_A$ do podprzestrzeni $W$. $W$ jest przestrzenią euklidesową (z iloczynem skalarnym indukowanym z $E^n$). Skoro $F_A$ jest symetryczne, to również $F'$ jest symetryczne. Niech ${\cal C}$ będzie bazą ortonormalną przestrzeni $W$. Na mocy uwagi 14.2, $m_{{\cal C}}(F')$ jest symetryczna, więc z uwagi 14.3 wynika, że ma ona wartość własną, ktora jest również wartością własną $F'$, $F_A$ i macierzy $A$.

Wniosek 14.5   Jeśli $F:V\rightarrow V$ jest symetryczne, to $F$ ma wartość własną.

Dla dowodu diagonalizowalności macierzy symetrycznych wygodniej będzie dowieść najpierw diagonalizowalności przekształceń symetrycznych.

Twierdzenie 14.6   Jeśli przekształcenie liniowe $F:V\rightarrow V$ jest symetryczne, to $F$ jest diagonalizowalne. Więcej, istnieje ortonormalna baza przestrzeni $V$ złożona z wektorów własnych $F$.

Dowód. Dowód przeprowadzimy przez indukcję względem $n=\dim(V)$. Przypuśćmy więc, że nasze twierdzenie jest słuszne dla wszystkich przestrzeni euklidesowych wymiaru $<n$, udowodnimy je dla przestrzeni $V$.

Niech $\lambda$ będzie wartością własną $F$ (wniosek 14.5), niech $V^{\lambda}$ będzie przestrzenią wektorów własnych $F$ dla wartości własnej $\lambda$. Przestrzeń $V^{\lambda}$ ma wymiar $>0$ i jest $F$-niezmiennicza (por. komentarz do definicji 8.10). Jeżeli $V^{\lambda}=V$, to $F=\lambda\cdot id$ i ma macierz diagonalną $\lambda\cdot I$ w dowolnej bazie przestrzeni $V$. Załóżmy więc, że

$$0<\dim(V^{\lambda})<n.$$

Niech $V'= (V^{\lambda})^{\perp}$. Na mocy uwagi 11.3, $V=V^{\lambda}\oplus V'$. $\dim(V)=\dim(V^{\lambda})+\dim(V')$, więc również

$$0<\dim(V')<n.$$

Pokażemy, że $V'$ jest również $F$-niezmiennicza. Niech $w\in V'$. Wystarczy pokazać, że $F(w)\in V'$, tzn. $\langle F(w),v\rangle=0$ dla wszystkich $v\in V^{\lambda}$. Dla takich wektorów $v,w$ mamy $\langle w,v\rangle=0$ i $F(v)=\lambda v$, więc korzystając z symetryczności $F$ dostajemy

$$\langle F(w),v\rangle=\langle w,F(v)\rangle=\langle w,tv\rangle=t\langle w,v\rangle=0.$$

Rozważając przekształcenia symetryczne powstałe przez obcięcie $F$ do podprzestrzeni $V^{\lambda}$ i $V'$, na mocy założenia indukcyjnego dostajemy bazy ortonormalne ${\cal B}_1$ i ${\cal B}_2$ przestrzeni $V^{\lambda}$ i $V'$ odpowiednio, złożone z wektorów własnych $F$. Dlatego ${\cal B}={\cal B}_1\cup{\cal B}_2$ jest bazą ortonormalną przestrzeni $V$ złożoną z wektorów własnych $F$.

Wniosek 14.7   Macierz symetryczna $A$ (wymiaru $n\times n$) jest diagonalizowalna. Więcej, istnieje macierz ortogonalna $C$ taka, że macierz $C^{-1}AC$ jest diagonalna.

Dowód. Niech $F_A:E^n\rightarrow E^n$ będzie przekształceniem liniowym o macierzy $A$. $F_A$ jest symetryczne (uwaga 14.2), więc na mocy twierdzenia 14.6 istnieje ortonormalna baza ${\cal B}$ przestrzeni $E^n$ złożona z wektorów własnych $F_A$. $m_{{\cal B}}(F_A)$ jest diagonalna i

$$m_{{\cal B}}(F_A)=C^{-1}AC,$$

gdzie $C=m_{{\cal B}{\cal E}}(id)$ i $A=m_{{\cal E}}(F_A)$. Standardowa baza ${\cal E}$ jest ortonormalna, więc macierz $C$ jest ortogonalna (ćwiczenie).

Do znajdowania bazy ortonormalnej złożonej z wektorów własnych przekształcenia symetrycznego przydatna być może następująca uwaga.

Uwaga 14.8   Jeśli $F:V\rightarrow V$ jest symetryczne, $\lambda_1\neq\lambda_2$ są dwiema wartościami własnymi $F$, $F(v)=\lambda_1 v$ i $F(w)=\lambda_2 w$, to $v\perp w$.

Dowód. ćwiczenie.

Wniosek 14.9   Załóżmy, że $\lambda_1,\dots,\lambda_k$ są różnymi wartościami własnymi przekształcenia symetrycznego $F:V\rightarrow V$. Wtedy przestrzenie wektorów własnych $V^{\lambda_1},\dots,V^{\lambda_k}$ są parami ortogonalne.

Na mocy twierdzenia 8.11, przy oznaczeniach z wniosku 14.9, $V=V^{\lambda_1}\oplus\cdots\oplus V^{\lambda_k}$. Niech ${\cal B}_i$ będzie bazą ortonormalną przestrzeni $V^{\lambda_i},\ i=1,\dots,k$. Wówczas na mocy wniosku 14.9, ${\cal B}={\cal B}_1\cup\dots\cup{\cal B}_k$ jest bazą ortonormalną $V$ złożoną z wektorów własnych $F$.

W dalszej części tego rozdziału zajmiemy się formami kwadratowymi i funkcjonałami kwadratowymi. Formą kwadratową zmiennych $x_1,\dots,x_n$ nazywamy dowolną sumę jednomianów stopnia $2$ , zmiennych $x_1,\dots,x_n$.

Na przykład, formą kwadratową jest wielomian $Q(x_1,x_2,x_3)=x_1^2+2x_1x_3+x_2^2.$ Wielomian ten określa funkcję $Q:{\mathbb{R}}^n\rightarrow {\mathbb{R}}$, zwaną funkcjonałem kwadratowym na przestrzeni ${\mathbb{R}}^n$. Zauważmy, że w tym przykładzie $Q(x_1,x_2,x_3)=\Phi((x_1,x_2,x_3),(x_1,x_2,x_3))$, gdzie $\Phi$ jest symetryczną formą 2-liniową daną wzorem

$$\Phi((x_1,x_2,x_3),(y_1,y_2,y_3))=x_1y_1+x_1y_3+x_3y_1+x_2y_2.$$

Jedną z motywacji do zajmowania się formami i funkcjonałami kwadratowymi jest chęć zrozumienia, jakie podzbiory w ${\mathbb{R}}^n$ są opisane przez równania typu $Q(x_1,\dots,x_n)=0$ lub $Q(x_1,\dots,x_n)=1$, gdzie $Q$ jest formą kwadratową zmiennych $x_1,\dots,x_n$. W przypadku przestrzeni ${\mathbb{R}}^2$ i ${\mathbb{R}}^3$ rozważania te prowadziły do klasyfikacji krzywych stożkowych i kwadryk. Metoda polegała tam na dobraniu pewnego nowego układu współrzędnych, w którym równanie danej krzywej czy powierzchni było proste. Podobnie zrobimy również w przypadku przestrzeni ${\mathbb{R}}^n$. Wygodnie jest jednak rozważać funkcjonały kwadratowe na dowolnej przestrzeni liniowej $V$ wymiaru $n$.

Powyżej zauważyliśmy już, że formy kwadratowe związane są z formami 2-liniowymi. Ten związek sugeruje następującą definicję.

Definicja 14.10   $Q:V\rightarrow {\mathbb{R}}$ jest funkcjonałem kwadratowym, gdy istnieje pewien symetryczny funkcjonał 2-liniowy $\Phi:V\times V\rightarrow {\mathbb{R}}$ taki, że $Q(v)=\Phi(v,v)$ dla wszystkich $v\in V$.

Uwaga 14.11   Funkcjonał 2-liniowy $\Phi$ z definicji 14.10 jest wyznaczony jednoznacznie przez $Q$.

Dowód. Niech $v,w\in V$. Korzystając z 2-liniowości i symetryczności $\Phi$ dostajemy $Q(v+w)=$

$$\Phi(v+w,v+w)=\Phi(v,v)+\Phi(w,w)+2\Phi(v,w)=Q(v)+Q(w)+2\Phi(v,w).$$

Dlatego $\Phi(v,w)=\frac{1}{2}(Q(v+w)-Q(v)-Q(w))$.

Niech ${\cal C}$ będzie dowolną bazą przestrzeni $V$ i niech $A=m_{{\cal C}}(\Phi)$ będzie macierzą symetrycznego funkcjonału 2-liniowego odpowiadającego funkcjonałowi kwadratowemu $Q$. Macierz $A$ jest symetryczna.

Załóżmy, że $v=\sum t_ic_i\in V$. Wtedy $Q(v)=\sum_{i,j}a_{ij}t_it_j$.

Formę kwadratową $\sum_{i,j}a_{ij}x_ix_j$ nazywamy formą funkcjonału $Q$ w bazie ${\cal C}$, zaś macierz $A$ macierzą funkcjonału $Q$ w bazie ${\cal C}$. Na przykład macierz

$$\left[\begin{array}{ccc}1&0&1 0&1&0 1&0&0\end{array}\right]$$

jest macierzą w bazie standardowej funkcjonału określonego formą
$Q(x_1,x_2,x_3)=x_1^2+2x_1x_3+x_2^2$.

Podobnie jak w przypadku diagonalizacji przekształceń liniowych dążymy zazwyczaj do znalezienia bazy, w której dany funkcjonał kwadratowy ma prostą macierz. Okazuje się, że w przypadku przestrzeni euklidesowej każdy funkcjonał kwadratowy ma macierz diagonalną w pewnej bazie ortonormalnej.

Twierdzenie 14.12   Załóżmy, że $(V,\langle\cdot,\cdot\rangle)$ jest przestrzenią euklidesową wymiaru $n$, zaś $Q:V\rightarrow {\mathbb{R}}$ jest funkcjonałem kwadratowym. Wtedy w pewnej bazie ortonormalnej ${\cal B}$ przestrzeni $V$, $Q$ ma macierz diagonalną

$$\left[\begin{array}{ccc}a_1&\mbox{}&0\\ \mbox{}&\ddots&\mbox{}\\ 0&\mbox{}&a_n\end{array}\right]$$

i wtedy dla każdego $v\in V$ mamy $Q(v)=\sum a_iu_i^2$, gdzie

$$[v]_{{\cal B}}=\left[\begin{array}{c}u_1 \vdots\\ u_n\end{array}\right].$$

Formę kwadratową $\sum a_iu_i^2$ z twierdzenia 14.12 nazywamy formą kanoniczną funkcjonału $Q$.
Dowód. Niech ${\cal C}$ będzie pewną bazą ortonormalną przestrzeni $V$. Niech $\Phi$ będzie symetrycznym 2-liniowym funkcjonałem na $V$ związanym z $Q$ oraz niech $B=m_{{\cal C}}(\Phi)$. Macierz $B$ jest symetryczna. Niech $F:V\rightarrow V$ będzie przekształceniem liniowym o macierzy $B$ w bazie ${\cal C}$. $F$ jest symetryczne na mocy uwagi 4.2. Z twierdzenia 14.6 wynika, że istnieje baza ortonormalna ${\cal B}$ przestrzeni $V$, w ktorej macierz $m_{{\cal B}}(F)$ jest diagonalna, tzn.

$$m_{{\cal B}}(F)=\left[\begin{array}{ccc}a_1&\mbox{}&0\\ \mbox{}&\ddots&\mbox{}\\ 0&\mbox{}&a_n\end{array}\right]$$

dla pewnych $a_1,\dots,a_n\in {\mathbb{R}}$. Mamy $m_{{\cal B}}(F)=C^{-1}BC$, gdzie $C=m_{{\cal C}{\cal B}}(id)$. Bazy ${\cal B},{\cal C}$ są ortogonalne, więc macierz przejścia $C$ jest ortogonalna i $C^{-1}=C^*$. Dlatego $m_{{\cal B}}(\Phi)=C^*BC=m_{{\cal B}}(F)$ jest diagonalna.

Rozważmy formę kwadratową $Q=\sum_{i,j}a_{ij}x_ix_j$ (dla pewnej symetrycznej macierzy $[a_{ij}]_{n\times n}$) i związany z nią funkcjonał kwadratowy $Q:{\mathbb{R}}^n\rightarrow {\mathbb{R}}$.

Wniosek 14.13   W pewnym nowym prostokątnym układzie współrzędnych $Ou_1\dots u_n$ w ${\mathbb{R}}^n$ funkcjonał $Q$ wyraża się wzorem $Q(X)=\sum_{i=1}^n c_iu_i^2$, gdzie $u_1,\dots,u_n$ są nowymi współrzędnymi wektora $X$.

Dowód. Układ współrzędnych $Ou_1\dots u_n$ jest generowany przez ortonormalną bazę ${\cal B}$ przestrzeni $V=E^n$ z twierdzenia 14.12.

Przykład.

Znajdziemy kanoniczną postać formy kwadratowej $Q(x_1,x_2,x_3,x_4)=2x_1x_2+2x_1x_3+2x_2x_4$. W bazie standardowej przestrzeni ${\mathbb{R}}^n$ forma ta ma macierz

$$A=\left[\begin{array}{cccc}0&1&1&0\\ 1&0&0&1\\ 1&0&0&0 \ 0&1&0&0\end{array}\right].$$

Szukamy wartości własnych macierzy $A$. By wyliczyć poniższy wyznacznik stosujemy rozwinięcie Laplace'a względem 4. kolumny.

$$\varphi_A(X)=\det\left[\begin{array}{rrrr}-X&1&1&0\\ 1&-X&0&1\\ 1&0&-X&0 \ 0&1&0&-X\end{array}\right] =$$

$$(-1)^{2+4}\cdot 1\cdot\left\vert\begin{array}{rrr}-X&1&1 1&... ...egin{array}{rrr}-X&1&1\\ 1&-X&0 1&0&-X\end{array}\right\vert$$

$$=1-X^2+(-X)\cdot[(-X)^3-(-X)-(-X))=1-3X^2+X^4.$$

Wartości własne macierzy $A$ to pierwiastki tego wielomianu.

$$\lambda_1=\sqrt{\frac{3-\sqrt{5}}{2}},\ \lambda_2=-\sqrt{\fra... ...\frac{3+\sqrt{5}}{2}}, \lambda_4=-\sqrt{\frac{3+\sqrt{5}}{2}}.$$

Dlatego w pewnym nowym prostokątnym układzie współrzędnych funkcjonał $Q$ ma formę

$$Q(X)=\lambda_1u_1^2+\lambda_2u_2^2+\lambda_3u_3^2+\lambda_4u_4^2,$$

gdzie $u_1,u_2,u_3,u_4$ to nowe współrzędne wektora $X$. Nowy układ współrzędnych generowany jest przez jednostkowe ortogonalne (uwaga 14.8) wektory własne $U_1,U_2,U_3,U_4$ macierzy $A$ dla wartości własnych $\lambda_1,\lambda_2,\lambda_3,\lambda_4$.

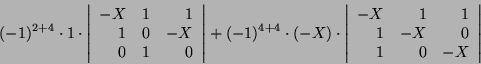
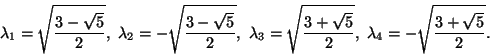
Używając formy kanonicznej funkcjonału $Q$ możemy łatwiej wyobrazić sobie hiperpowierzchnie dane równaniami $Q(X)=0$ i $Q(X)=1$.