Załóżmy, że
![]() . Zbiór
. Zbiór
![\begin{displaymath}[v_1,\dots,v_n]=\left\{\sum_{i=1}^nt_iv_i:0\leq t_i\leq 1\right\}\end{displaymath}](img1900.png)
Gdy wektory ![]() są liniowo niezależne i
są liniowo niezależne i ![]() , zbiór
, zbiór
![]() jest zwykłym równoległościanem (dla
jest zwykłym równoległościanem (dla ![]() ) lub
równoległobokiem (dla
) lub
równoległobokiem (dla ![]() ) o wierzchołkach
) o wierzchołkach
![]() .
.
Zwróćmy uwagę, że rzut prostopadły na podprzestrzeń
![]() istnieje, gdyż podprzestrzeń ta ma
skończony wymiar, więc ma bazę ortonormalną (twierdzenie 11.1,
uwaga 10.9). Ponadto liczba
istnieje, gdyż podprzestrzeń ta ma
skończony wymiar, więc ma bazę ortonormalną (twierdzenie 11.1,
uwaga 10.9). Ponadto liczba ![]() to odległość wektora
to odległość wektora
![]() od podprzestrzeni
od podprzestrzeni ![]() (rozdział 11).
(rozdział 11).
Rozważmy szczególny przypadek, gdy ![]() i
i
![]() jest
standardową bazą ortonormalną. Wówczas kolumny macierzy
jest
standardową bazą ortonormalną. Wówczas kolumny macierzy
![]() w fakcie 15.2(2) to po prostu wektory
w fakcie 15.2(2) to po prostu wektory ![]() . Fakt ten
potwierdza zatem naszą intuicję dotyczącą wyznacznika w rozdziale
5.
. Fakt ten
potwierdza zatem naszą intuicję dotyczącą wyznacznika w rozdziale
5.
Dowód faktu 15.2.
1) Skoro ![]() są liniowo zależne, to dla pewnego
są liniowo zależne, to dla pewnego ![]() wektor
wektor ![]() jest liniową kombinacją wektorów
jest liniową kombinacją wektorów
![]() . Dlatego jest on równy swojemu rzutowi
. Dlatego jest on równy swojemu rzutowi ![]() na
podprzestrzeń
na
podprzestrzeń
![]() . Wtedy
. Wtedy
![]() i zgodnie z definicją
15.1,
i zgodnie z definicją
15.1,
2) Stosujemy indukcję względem ![]() . Dla
. Dla ![]() teza jest
oczywista. Załóżmy, że
teza jest
oczywista. Załóżmy, że ![]() i teza jest udowodniona dla
i teza jest udowodniona dla ![]() .
.
Niech
![]() . Zbiór
. Zbiór
![]() jest
bazą przestrzeni
jest
bazą przestrzeni ![]() i
i
![]() . Zauważmy, że
. Zauważmy, że ![]() nie zależy od wyboru bazy
nie zależy od wyboru bazy ![]() przestrzeni
przestrzeni ![]() . Istotnie, załóżmy,
że
. Istotnie, załóżmy,
że ![]() jest inną bazą ortonormalną przestrzeni
jest inną bazą ortonormalną przestrzeni ![]() . Wtedy macierz
. Wtedy macierz
![]() jest ortogonalna, więc
jest ortogonalna, więc
![]() (wniosek 11.13). Mamy
(wniosek 11.13). Mamy
![]() , więc
, więc
![]() .
.
Stosując metodę ortonormalizacji Grama-Schmidta, możemy wybrać
bazę ortonormalną
![]() przestrzeni
przestrzeni ![]() tak,
że zbiór
tak,
że zbiór
![]() jest bazą przestrzeni
jest bazą przestrzeni ![]() . Niech
. Niech
![]() będzie rzutem prostopadłym wektora
będzie rzutem prostopadłym wektora ![]() na przestrzeń
na przestrzeń
![]() .
.
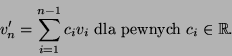
Niech
![]() , gdzie
, gdzie
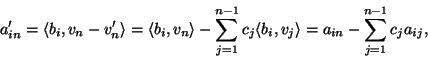
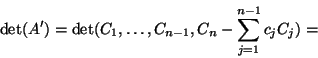
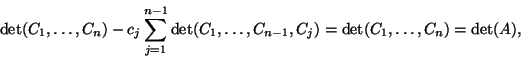
Następny wniosek dostarcza innego sposobu obliczania objętości uogólnionego równoległościanu.
Załóżmy więc, że ![]() są liniowo niezależne. Niech
są liniowo niezależne. Niech
![]() będzie bazą ortonormalną przestrzeni
będzie bazą ortonormalną przestrzeni
![]() i niech
i niech
![]() . Na mocy
uwagi 10.8 i faktu 15.2 mamy
. Na mocy
uwagi 10.8 i faktu 15.2 mamy
![\begin{displaymath}v_j=\sum_{i=1}^na_{ij}b_i\mbox{ i
}vol[v_1,\dots,v_n]=\vert\det[a_{ij}]\vert.\end{displaymath}](img1960.png)
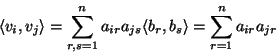
Wyznacznik
![]() występujący we wniosku 15.3 nazywamy
wyznacznikem Grama układu wektorów
występujący we wniosku 15.3 nazywamy
wyznacznikem Grama układu wektorów ![]() .
.