Przypomnijmy (rozdział 3), że funkcjonałem liniowym na przestrzeni
![]() nazywamy dowolne przekształcenie liniowe
nazywamy dowolne przekształcenie liniowe
![]() . Przestrzeń funkcjonałów liniowych
. Przestrzeń funkcjonałów liniowych
![]() oznaczamy przez
oznaczamy przez
![]() , nazywamy ją przestrzenią sprzężoną (lub: dualną) do
, nazywamy ją przestrzenią sprzężoną (lub: dualną) do ![]() (rozdział 4).
(rozdział 4).
W tym rozdziale zakładamy, że ![]() jest przestrzenią liniową
wymiaru
jest przestrzenią liniową
wymiaru ![]() . załóżmy, że
. załóżmy, że
![]() jest bazą
jest bazą
![]() . Przy pomocy tej bazy skonstruujemy bazę
. Przy pomocy tej bazy skonstruujemy bazę
![]() przestrzeni
przestrzeni ![]() . Mianowicie definiujemy
. Mianowicie definiujemy
![]() jako jedyny fukcjonał liniowy na
jako jedyny fukcjonał liniowy na ![]() taki, że
taki, że

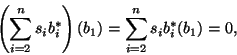
b) Generowanie ![]() . Niech
. Niech ![]() oraz
oraz ![]() dla
dla
![]() . Wówczas funkcjonały
. Wówczas funkcjonały ![]() i
i ![]() zgadzają
się na wektorach bazowych
zgadzają
się na wektorach bazowych
![]() , więc są równe.
, więc są równe.
W rozdziale 4 zauważyliśmy już, że przestrzenie ![]() i
i ![]() mają
ten sam wymiar, więc są izomorficzne. Przy użyciu bazy sprzężonej
mają
ten sam wymiar, więc są izomorficzne. Przy użyciu bazy sprzężonej
![]() możemy jawnie zdefiniować izomorfizm
możemy jawnie zdefiniować izomorfizm
![]() wzorem
wzorem
W przypadku przestrzeni euklidesowej ![]() możemy określić izomorfizm
możemy określić izomorfizm
![]() w sposób bardziej naturalny. Mianowicie, dla
w sposób bardziej naturalny. Mianowicie, dla
![]() definiujemy
definiujemy ![]() wzorem
wzorem
![]() . Sprawdzenie, że
. Sprawdzenie, że ![]() jest izomorfizmem, pozostawiamy jako
ćwiczenie. Izomorfizm ten nazywa się izomorfizmem Frecheta-Riesza.
jest izomorfizmem, pozostawiamy jako
ćwiczenie. Izomorfizm ten nazywa się izomorfizmem Frecheta-Riesza.
Okazuje się, że uwaga 13.2 nie jest prawdziwa dla przestrzeni ![]() nieskończonego wymiaru.
nieskończonego wymiaru.
Przykłady.
1. Wielomian postaci
![]() gdzie
gdzie
![]() , nazywamy formą liniową. Wielomian ten w
naturalny sposób określa funkcjonał liniowy
, nazywamy formą liniową. Wielomian ten w
naturalny sposób określa funkcjonał liniowy
![]() .
.
2. Ogólniej, załóżmy, że
![]() jest liniowe i
jest liniowe i
![]() . Niech
. Niech ![]() . Wtedy
. Wtedy
W algebrze liniowej obok przekształceń i funkcjonałów liniowych
rozpatruje się również przekształcenia i funkcjonały
wieloliniowe. Funkcjonałem ![]() -liniowym na przestrzeni
-liniowym na przestrzeni ![]() nazywamy
dowolną funkcję
nazywamy
dowolną funkcję
1.1'.
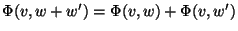
2.2'.

Załóżmy teraz, że
![]() jest dowolną
funkcją. Dla
jest dowolną
funkcją. Dla ![]() definiujemy funkcje
definiujemy funkcje
![]() i
i
![]() wzorami
wzorami
Z funkcjonałem 2-liniowym
![]() wiążemy
przekształcenia liniowe
wiążemy
przekształcenia liniowe
![]() określone
wzorami
określone
wzorami
Wielomian
![]() nazywamy formą
2-liniową zmiennych
nazywamy formą
2-liniową zmiennych ![]() . Wielomian ten definiuje funkcjonał
2-liniowy
. Wielomian ten definiuje funkcjonał
2-liniowy
![]() wyznaczony przez macierz
wyznaczony przez macierz
![]() . Okazuje się, że dowolnemu funkcjonałowi
2-liniowemu
. Okazuje się, że dowolnemu funkcjonałowi
2-liniowemu
![]() możemy przypisać pewną
macierz, przy pomocy której możemy obliczac wartośći
możemy przypisać pewną
macierz, przy pomocy której możemy obliczac wartośći ![]() .
Niech
.
Niech
![\begin{displaymath}[v]_{{\cal B}}=\left[\begin{array}{c}t_1 \vdots\\
t_n\end{...
...}}=\left[\begin{array}{c}s_1 \vdots\\
s_n\end{array}\right].\end{displaymath}](img1724.png)
Podobnie jak w przypadku macierzy przekształceń liniowych
zbadamy teraz, jak zmienia się macierz funkcjonału 2-liniowego
![]() przy zmianie bazy przestrzeni
przy zmianie bazy przestrzeni ![]() . Załóżmy, że
. Załóżmy, że
![]() jest
inną bazą przestrzeni
jest
inną bazą przestrzeni ![]() .
.
Niech ![]() . Wówczas
. Wówczas
Zwróćmy uwagę, że funkcjonał ![]() określony na początku
tego rozdziału ma macierz
określony na początku
tego rozdziału ma macierz ![]() w bazie standardowej
w bazie standardowej ![]() przestrzeni
przestrzeni
![]() .
.
W szczególności możemy krótko zdefiniować iloczyn skalarny w
przestrzeni ![]() jako dowolny symetryczny dodatnio określony
funkcjonał 2-liniowy na przestrzeni
jako dowolny symetryczny dodatnio określony
funkcjonał 2-liniowy na przestrzeni ![]() . Zatem, by sprawdzić, czy
funkcjonał
. Zatem, by sprawdzić, czy
funkcjonał ![]() jest iloczynem skalarnym w przestrzeni
jest iloczynem skalarnym w przestrzeni
![]() ,
wystarczy sprawdzić, czy jest on symetryczny i dodatnio określony.
,
wystarczy sprawdzić, czy jest on symetryczny i dodatnio określony.
![]() . Jeśli
. Jeśli ![]() jest symetryczny, to
jest symetryczny, to
![]() , więc macierz
, więc macierz ![]() jest
symetryczna.
jest
symetryczna.
![]() . Załóżmy, że macierz
. Załóżmy, że macierz ![]() jest symetryczna. Niech
jest symetryczna. Niech
![]() . Wtedy
. Wtedy
Dowód (2) pozostawiamy jako ćwiczenie.
Sprawdzenie, czy dana macierz jest symetryczna, jest łatwe. Do
sprawdzenia, czy dana macierz symetryczna
![]() jest dodatnio określona, służy kryterium Sylvestera, które
opiszemy poniżej.
jest dodatnio określona, służy kryterium Sylvestera, które
opiszemy poniżej.
Niech ![]() będzie fragmentem macierzy
będzie fragmentem macierzy ![]() złożonym z wyrazów
złożonym z wyrazów
![]() .
.
Przykład.
Używając kryterium Sylvestera łatwo sprawdzić, czy funkcjonał
![]() jest iloczynem skalarnym. Na przykład rozważmy macierze symetryczne
jest iloczynem skalarnym. Na przykład rozważmy macierze symetryczne
![\begin{displaymath}A=\left[\begin{array}{ccc}1&0&0 0&2&1 0&1&3\end{array}\ri...
...left[\begin{array}{ccc}0&2&0 2&1&0 0&0&3\end{array}\right].\end{displaymath}](img1746.png)
Dowód twierdzenia 13.9. ![]() . Załóżmy, że
. Załóżmy, że
![]() jest dodatnio określona. Wtedy funkcjonał
jest dodatnio określona. Wtedy funkcjonał
![]() jest iloczynem skalarnym. Pokażemy, że
jest iloczynem skalarnym. Pokażemy, że
![]() dla wszystkich
dla wszystkich ![]() .
.
Niech
![]() będzie bazą standardową przestrzeni
będzie bazą standardową przestrzeni
![]() .
.
Dla ![]() definiujemy
definiujemy
![]() , gdzie
, gdzie
![]() . Stosując do
bazy
. Stosując do
bazy ![]() metodę Grama-Schmidta (twierdzenie 11.1) (w przestrzeni
euklidesowej
metodę Grama-Schmidta (twierdzenie 11.1) (w przestrzeni
euklidesowej ![]() ), znajdujemy bazę ortonormalną
), znajdujemy bazę ortonormalną
![]() przestrzeni
przestrzeni
![]() taką, że
taką, że
![]() jest bazą przestrzeni
jest bazą przestrzeni ![]() (
(![]() ).
).
Oznaczmy przez ![]() funkcjonał 2-liniowy na przestrzeni
funkcjonał 2-liniowy na przestrzeni ![]() powstały przez ograniczenie funkcjonału
powstały przez ograniczenie funkcjonału ![]() . Zwróćmy uwagę,
że
. Zwróćmy uwagę,
że
![]() . Ponadto skoro baza
. Ponadto skoro baza ![]() jest ortonormalna
w
jest ortonormalna
w
![]() , to
, to
![]() .
Na mocy faktu 13.5 mamy więc
.
Na mocy faktu 13.5 mamy więc
![]() , gdzie
, gdzie
![]() , więc na
mocy wniosku 5.13 i twierdzenia 5.14
, więc na
mocy wniosku 5.13 i twierdzenia 5.14
![]() . Tę część dowodu przeprowadzimy przez indukcję
względem
. Tę część dowodu przeprowadzimy przez indukcję
względem ![]() . Dla
. Dla ![]() teza jest oczywista. Załóżmy więc, że
twierdzenie jest słuszne dla
teza jest oczywista. Załóżmy więc, że
twierdzenie jest słuszne dla ![]() , udowodnimy je dla
, udowodnimy je dla ![]() .
.
Załóżmy, że ![]() jest macierzą symetryczną wymiaru
jest macierzą symetryczną wymiaru
![]() oraz
oraz ![]() dla wszystkich
dla wszystkich ![]() . Pokażemy,
że funkcjonał
. Pokażemy,
że funkcjonał
![]() jest
dodatnio określony. Wiemy już, że
jest
dodatnio określony. Wiemy już, że ![]() jest symetryczny. Z założenia indukcyjnego wynika, że macierz
jest symetryczny. Z założenia indukcyjnego wynika, że macierz
![]() jest symetryczna i dodatnio określona.
jest symetryczna i dodatnio określona.
Niech
![]() będzie bazą standardową
będzie bazą standardową
![]() i
niech
i
niech
![]() , gdzie
, gdzie
![]() . Niech
. Niech ![]() będzie obcięciem funkcjonału
będzie obcięciem funkcjonału ![]() do przestrzeni
do przestrzeni ![]() .
.
![]() , więc funkcjonał
, więc funkcjonał ![]() jest iloczynem skalarnym
w przestrzeni
jest iloczynem skalarnym
w przestrzeni ![]() . Niech
. Niech
![]() będzie bazą
ortonormalną przestrzeni euklidesowej
będzie bazą
ortonormalną przestrzeni euklidesowej ![]() . Niech
. Niech
Przypuśćmy nie wprost, że
![]() . Wybierzmy
niezerowy wektor
. Wybierzmy
niezerowy wektor
![]() . Wtedy
. Wtedy
![]() , co przeczy temu, że
, co przeczy temu, że ![]() jest iloczynem
skalarnym na
jest iloczynem
skalarnym na ![]() .
.
By dowieść, że
![]() , wybieramy dowolny wektor
, wybieramy dowolny wektor
![]() . Niech
. Niech
![]() . Wektor
. Wektor
![]() jest określony podobnie jak rzut prostopadły wektora
jest określony podobnie jak rzut prostopadły wektora ![]() na
podprzestrzeń
na
podprzestrzeń ![]() (w przestrzeni euklidesowej). Podobnie jak w
dowodzie 10.9(3) można dowieść, że
(w przestrzeni euklidesowej). Podobnie jak w
dowodzie 10.9(3) można dowieść, że
![]() dla
wszystkich
dla
wszystkich ![]() . Dlatego
. Dlatego
![]() , czyli
, czyli
![]() .
.
Z ![]() wynika, że
wynika, że
![]() .
.
Niech teraz ![]() będzie dowolnym niezerowym wektorem przestrzeni
będzie dowolnym niezerowym wektorem przestrzeni
![]() . By zakończyć dowód, wystarczy pokazać, że
. By zakończyć dowód, wystarczy pokazać, że
![]() .
.
Przypadek 1. ![]() . W tym przypadku
. W tym przypadku
![]() , gdyż
, gdyż ![]() jest iloczynem skalarnym w
przestrzeni
jest iloczynem skalarnym w
przestrzeni ![]() .
.
Przypadek 2.
![]() . Niech
. Niech ![]() i
i
![]() . Wtedy
. Wtedy
![]() jest bazą
jest bazą
![]() taką,
że dla
taką,
że dla
![]() . Ponadto dla
. Ponadto dla
![]() (bo
(bo ![]() jest bazą
ortonormalną
jest bazą
ortonormalną ![]() ).
).
![]() jest macierzą
diagonalną, na głównej przekątnej jest ciąg
jest macierzą
diagonalną, na głównej przekątnej jest ciąg ![]() jedynek i
jedynek i
![]() . Dlatego
. Dlatego
![]() .
.
Z założenia
![]() (gdyż
(gdyż
![]() .) Podobnie jak w dowodzie
.) Podobnie jak w dowodzie ![]() ,
,
Przypadek 3. ![]() i
i
![]() Na mocy
Na mocy ![]() ,
,
![]() dla pewnych niezerowych
dla pewnych niezerowych
![]() . Mamy
. Mamy
![]() i
i
![]() (na mocy przypadków 1. i 2.). Dlatego
(na mocy przypadków 1. i 2.). Dlatego