


Next: 6. Wyznacznik, zmiana bazy
Up: Algebra liniowa II
Previous: 4. Przekształcenia liniowe i
Niech  będzie macierzą wymiaru
będzie macierzą wymiaru 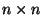 , o kolumnach
, o kolumnach
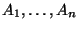 . Piszemy wówczas
. Piszemy wówczas
 . W tym rozdziale
zajmiemy się problemem, jak sprawdzić, czy macierz
. W tym rozdziale
zajmiemy się problemem, jak sprawdzić, czy macierz  jest
odwracalna. Na mocy wniosku 4.14 jest to równoważne temu, że
wektory
jest
odwracalna. Na mocy wniosku 4.14 jest to równoważne temu, że
wektory 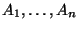 są liniowo niezależne w przestrzeni
są liniowo niezależne w przestrzeni
 .
Wektory te rozpinają w przestrzeni
.
Wektory te rozpinają w przestrzeni
 uogólniony
równoległościan
uogólniony
równoległościan
W przypadku 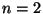 ,
,  jest równoległobokiem, w przypadku
jest równoległobokiem, w przypadku 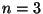 ,
,
 jest zwykłym równoległościanem (być może zdegenerowanym).
jest zwykłym równoległościanem (być może zdegenerowanym).
Rysunek:
Równoległobok  rozpięty przez
rozpięty przez 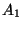 i
i 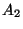
|
|
Intuicyjnie jest jasne, że wektory 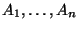 są liniowo
niezależne
są liniowo
niezależne 
 -wymiarowa objętość ``równoległościanu''
-wymiarowa objętość ``równoległościanu''
 jest
jest  . Są wzory definiujące tę objętość, poznamy
je w rozdziale 15. Wygodniej jednak zdefiniować
. Są wzory definiujące tę objętość, poznamy
je w rozdziale 15. Wygodniej jednak zdefiniować  -wymiarową
objętość ``zorientowaną'' ``równoległościanu''
-wymiarową
objętość ``zorientowaną'' ``równoległościanu''  (o
wartościach dodatnich lub ujemnych), równą
co do wartości bezwzględnej zwykłej
(o
wartościach dodatnich lub ujemnych), równą
co do wartości bezwzględnej zwykłej  -wymiarowej
objętości. Rolę takiej zorientowanej objętości bedzie odgrywać
funkcja wyznacznika
-wymiarowej
objętości. Rolę takiej zorientowanej objętości bedzie odgrywać
funkcja wyznacznika
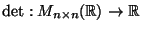 . Mówiąc nieformalnie, powinno być
. Mówiąc nieformalnie, powinno być
Funkcję wyznacznika wprowadzimy w sposób aksjomatyczny. Najpierw
wypiszemy postulowane własności funkcji 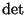 , następnie
udowodnimy, że istnieje dokładnie jedna funkcja o tych
własnościach. W rozdziale 15 udowodnimy, że tak określona funkcja
, następnie
udowodnimy, że istnieje dokładnie jedna funkcja o tych
własnościach. W rozdziale 15 udowodnimy, że tak określona funkcja
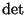 w istocie spełnia
w istocie spełnia 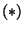 .
Macierze wymiaru
.
Macierze wymiaru 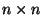 będziemy tu zapisywać
jako układy
będziemy tu zapisywać
jako układy  kolumn czy też wręcz układy
kolumn czy też wręcz układy  wektorów z
wektorów z
 . Zatem
. Zatem 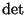 możemy uważać za n-argumentową funkcję o
argumentach z
możemy uważać za n-argumentową funkcję o
argumentach z
 i wartościach w
i wartościach w 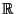 .
.
Oto postulowane własności wyznacznika.
- D1.
-

- D2.
- Dla
 ,
,

- D3.
- Jeśli dla pewnego
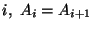 , to
, to
 .
.
- D4.
-
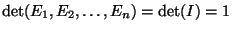
Rysunek:

|
|
Rysunek:
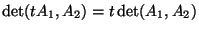
|
|
Jak wspomnieliśmy wyżej, pokażemy, że istnieje jedyna funkcja
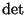 spelniająca D1-D4. Do tego celu będziemy potrzebować
pewnych wiadomości o permutacjach.
spelniająca D1-D4. Do tego celu będziemy potrzebować
pewnych wiadomości o permutacjach.
Definicja 5.1
Permutacją liczb
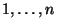
nazywamy
dowolną funkcję
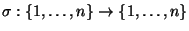
,
która jest 1-1 i ``na'' (tzn. jest bijekcją). Zbiór permutacji
liczb
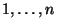
oznaczamy przez

.
Zauważmy, że zbiór  ma
ma 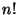 elementów. Permutację
elementów. Permutację
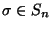 zapisujemy w postaci dwuwierszowej:
zapisujemy w postaci dwuwierszowej:
w dolnym wierszu występują wartości 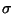 dla kolejnych liczb z
górnego wiersza.
dla kolejnych liczb z
górnego wiersza.
Permutacje (jak wszystkie funkcje) można składać. Złożenie
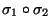 permutacji
permutacji
 jest
również permutacją z
jest
również permutacją z  . Składanie permutacji nazywamy też
mnożeniem permutacji i piszemy
. Składanie permutacji nazywamy też
mnożeniem permutacji i piszemy
 zamiast
zamiast
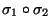 . Na przykład
. Na przykład
Szczególnym rodzajem permutacji są transpozycje. Dla
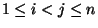 transpozycją
transpozycją 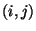 nazywamy permutację
nazywamy permutację
która zamienia miejscami 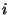 i
i  , nie ruszając innych
liczb. Jedną z permutacji z
, nie ruszając innych
liczb. Jedną z permutacji z  jest identyczność
jest identyczność
Przykład.
Niech
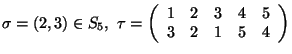 . Wówczas
. Wówczas
Ogólniej, jeśli 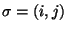 i
i  są dwiema permutacjami z
są dwiema permutacjami z
 , to
, to  powstaje z
powstaje z  przez zamianę (transpozycję) liczb
przez zamianę (transpozycję) liczb
 miejscami w permutacji
miejscami w permutacji
Uwaga 5.2
Każdą permutację można przedstawić jako iloczyn
pewnej liczby transpozycji liczb sąsiednich.
Dowód przeprowadzimy na przykładzie permutacji
W następującym ciągu kolejna permutacja powstaje przez
pomnożenie poprzedniej z prawej strony przez transpozycję nad
strzałką. W ciągu tym dążymy (poprzez przestawianie sąsiednich
liczb w dolnych wierszach) do osiągnięcia permutacji  .
.
To znaczy
Ale dla każdej
 . Zatem
. Zatem
Każda permutacja jest bijekcją. Dlatego funkcja odwrotna do
permutacji 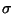 jest również bijekcją, czyli
permutacją. Nazywamy ją permutacją odwrotną do permutacji
jest również bijekcją, czyli
permutacją. Nazywamy ją permutacją odwrotną do permutacji 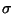 i oznaczamy przez
i oznaczamy przez 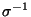 . Mamy
. Mamy
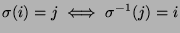 ,
dlatego odwracanie permutacji polega (w zapisie dwuwierszowym) na
zamianie miejscami wierszy górnego i dolnego:
,
dlatego odwracanie permutacji polega (w zapisie dwuwierszowym) na
zamianie miejscami wierszy górnego i dolnego:
po uporządkowaniu liczb w górnym wierszu uzyskujemy zwykły zapis
dwuwierszowy permutacji 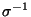 . Na przykład dla
. Na przykład dla
 ,
,
Dla transpozycji
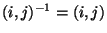 .
.
Definicja 5.3
Mówimy, że liczby

tworzą inwersję w permutacji
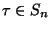
, jeśli w ciągu
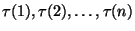
większa z liczb
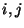
występuje wcześniej niż mniejsza.
Na przykład w permutacji
liczby 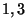 nie tworzą inwersji, zaś liczby
nie tworzą inwersji, zaś liczby  tworzą
inwersję. Pozostałe inwersje w
tworzą
inwersję. Pozostałe inwersje w  to
to
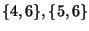 . Mówimy, że permutacja
. Mówimy, że permutacja  jest parzysta, gdy
występuje w niej parzyście wiele inwersji. W przeciwnym razie
mówimy, że
jest parzysta, gdy
występuje w niej parzyście wiele inwersji. W przeciwnym razie
mówimy, że  jest nieparzysta. Definiujemy znak permutacji
jest nieparzysta. Definiujemy znak permutacji
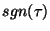 :
:
Uwaga 5.4
Transpozycja jest nieparzysta.
Na przykład w transpozycji
 tworzy inwersję z liczbami
tworzy inwersję z liczbami  , zaś
, zaś 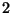 tworzy inwersję z
liczbami
tworzy inwersję z
liczbami 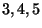 , przy czym w ten sposób inwersja
, przy czym w ten sposób inwersja 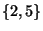 jest
liczona
jest
liczona 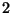 razy. Dlatego w transpozycji
razy. Dlatego w transpozycji 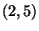 jest 5 inwersji.
jest 5 inwersji.
Uwaga 5.5
Jeśli
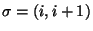
, to
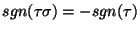
.
Dowód.  powstaje z
powstaje z  przez zamianę miejscami
przez zamianę miejscami
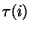 i
i  , więc liczba inwersji zmienia się o
, więc liczba inwersji zmienia się o  .
.
Uwaga 5.6
Dla permutacji
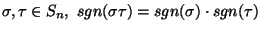
.
Dowód. Na mocy uwagi 5.2 przedstawiamy permutacje 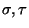 w
postaci iloczynów transpozycji liczb sąsiednich:
w
postaci iloczynów transpozycji liczb sąsiednich:
Permutacja 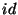 jest parzysta (ma
jest parzysta (ma 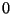 transpozycji).
Skoro mnożenie z prawej strony przez transpozycję liczb sąsiednich
zmienia znak permutacji (uwaga 5.5), to
transpozycji).
Skoro mnożenie z prawej strony przez transpozycję liczb sąsiednich
zmienia znak permutacji (uwaga 5.5), to
Dlatego
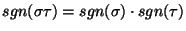 .
.
Uwaga 5.7
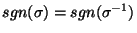
.
Dowód.
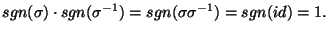
Wracamy teraz do wyznacznika.
Fakt 5.8
Załóżmy, że funkcja
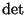
spełnia D1-D4. Wtedy
1) jeśli pewne

, to
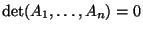
,
2) dla
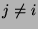
oraz
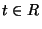
,
(indeks
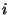
nad nawiasem klamrowym oznacza
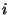
-tą kolumnę),
3) dla
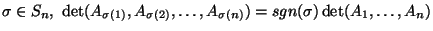
,
4) jeśli dla pewnych

, to
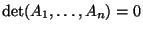
.
Dowód. 1) Gdy  , to
, to 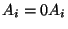 , zatem na mocy D2 (dla
, zatem na mocy D2 (dla
 ) dostajemy
) dostajemy
3) Na mocy D3,
Z drugiej strony, na mocy D1,
gdyż na mocy D3,
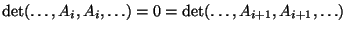 .
.
Dlatego
 , czyli
, czyli
Zatem (3) zachodzi dla szczególnego przypadku
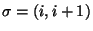 .
.
Niech teraz 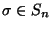 będzie dowolne. Na mocy uwagi 5.2
będzie dowolne. Na mocy uwagi 5.2
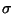 jest iloczynem transpozycji liczb sąsiednich:
jest iloczynem transpozycji liczb sąsiednich:
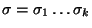 . Zatem
. Zatem
 powstaje z
powstaje z
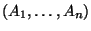 przez
przez 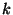 transpozycji kolumn sąsiednich, co zmienia znak
transpozycji kolumn sąsiednich, co zmienia znak 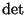
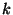 -razy. Gdy
-razy. Gdy 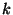 jest parzyste,
jest parzyste,  . Gdy
. Gdy 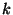 jest
nieparzyste,
jest
nieparzyste,
 . Stąd dostajemy (3).
. Stąd dostajemy (3).
4) Załóżmy, że 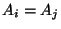 dla pewnych
dla pewnych  . Niech
. Niech
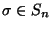 będzie permutacją taką, że
będzie permutacją taką, że 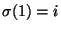 i
i
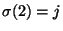 . Wówczas
. Wówczas
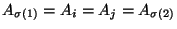 ,
więc na mocy D3 i (3)
,
więc na mocy D3 i (3)
Dlatego
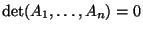 .
.
2) Na mocy D1 i D2:
gdyż
na mocy (4).
Następne twierdzenie jest kluczem do dowodu istnienia funkcji 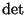 .
.
Twierdzenie 5.9
Załóżmy, że
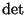
spełnia D1-D4,
![$A=[a_{ij}]_{n\times n},\
B=[b_{ij}]_{n\times n}$](img768.png)
. Wtedy
Dowód. Zapiszmy macierze  i
i  w postaci ciągów kolumn:
w postaci ciągów kolumn:

 . Wówczas dla
. Wówczas dla 
Dlatego
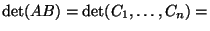
(na mocy D1-D3 oraz faktu 5.8)
W 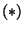 występuje wyznacznik
występuje wyznacznik
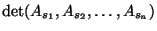 .
.
Dla ustalonego układu liczb
 definiujemy funkcję
definiujemy funkcję
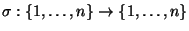 wzorem
wzorem 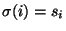 . Zwróćmy uwagę, że
. Zwróćmy uwagę, że
Jeśli w ciągu
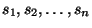 jedna z liczb powtarza się, to w
macierzy
jedna z liczb powtarza się, to w
macierzy
 pewne dwie kolumny są
równe, więc na mocy faktu 5.8(4) wówczas
pewne dwie kolumny są
równe, więc na mocy faktu 5.8(4) wówczas
Jeśli w ciągu
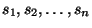 żadna liczba się nie powtarza,
to
żadna liczba się nie powtarza,
to 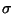 jest permutacją i na mocy faktu 5.8(3),
jest permutacją i na mocy faktu 5.8(3),
Dlatego w  sumowanie możemy ograniczyć do tych układów
sumowanie możemy ograniczyć do tych układów
 , które odpowiadają permutacjom
, które odpowiadają permutacjom
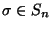 . Wówczas
. Wówczas
więc
Na mocy D4, 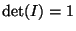 . Przyjmując w twierdzeniu 5.9
. Przyjmując w twierdzeniu 5.9 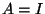 dostajemy
następujący wniosek.
dostajemy
następujący wniosek.
Wniosek 5.10
Jeśli
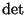
spełnia D1-D4, to
Używając tego wniosku możemy już udowodnić istnienie jedynej funkcji
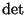 spełniającej D1-D4.
spełniającej D1-D4.
Twierdzenie 5.11
Istnieje dokładnie jedna funkcja
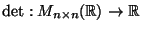
spełniająca D1-D4. Wyraża się ona wzorem

.
Dowód. (idea) Sprawdzamy rachunkowo, że funkcja 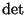 zadana
wzorem
zadana
wzorem  spełnia aksjomaty D1-D4. Jedyność wynika z
wniosku 5.10.
spełnia aksjomaty D1-D4. Jedyność wynika z
wniosku 5.10.
Z twierdzeń 5.9 i 5.11 wynika następujący wniosek.
Wniosek 5.12 (twierdzenie Cauchy'ego)
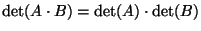
.
Kolejne twierdzenie pokazuje, że funkcja wyznacznika dostarcza
prostego kryterium do sprawdzania, czy macierz  jest odwracalna
(znalezienie takiego kryterium było celem tego rozdziału).
jest odwracalna
(znalezienie takiego kryterium było celem tego rozdziału).
Twierdzenie 5.13
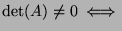
macierz

jest odwracalna.
Dowód.  Jeśli
Jeśli
 nie jest
odwracalna, to jej kolumny
nie jest
odwracalna, to jej kolumny 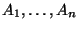 są liniowo zależne
(wniosek 4.14), więc na przykład
są liniowo zależne
(wniosek 4.14), więc na przykład
dla
pewnych
 (inne przypadki są analogiczne). Wtedy na mocy
D1,D2 i faktu 5.5(4)
(inne przypadki są analogiczne). Wtedy na mocy
D1,D2 i faktu 5.5(4)
 Załóżmy, że
Załóżmy, że  jest odwracalna. Wtedy istnieje macierz
odwrotna
jest odwracalna. Wtedy istnieje macierz
odwrotna  taka, że
taka, że
 . Z twierdzenia
Cauchy'ego dostajemy
. Z twierdzenia
Cauchy'ego dostajemy
 , więc
, więc
 .
.
Dowód twierdzenia 5.13 pokazuje, że
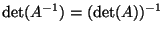 .
.
Transpozycją macierzy
![$A=[a_{ij}]_{n\times m}$](img803.png) nazywamy macierz
nazywamy macierz
![$A^*=[a^*_{ij}]_{m\times n}$](img804.png) , gdzie
, gdzie
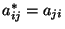 . Macierz
. Macierz  nazywamy też macierzą transponowaną względem
nazywamy też macierzą transponowaną względem  . Innymi słowy,
transpozycja polega na przestawieniu wierszy i kolumn danej macierzy.
Na przykład dla macierzy
. Innymi słowy,
transpozycja polega na przestawieniu wierszy i kolumn danej macierzy.
Na przykład dla macierzy
![$A=\left[\begin{array}{ccc}1&2&3\\
4&5&6\end{array}\right]$](img807.png) macierz transponowana ma postać
macierz transponowana ma postać
Okazuje się, że transpozycja nie zmienia wyznacznika macierzy.
Twierdzenie 5.14
Dla macierzy
![$A=[a_{ij}]_{n\times n},\
\det(A)=\det(A^*)$](img809.png)
.
Dowód. Niech
![$A^*=[a^*_{ij}]_{m\times n}$](img804.png) , gdzie
, gdzie
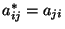 .
.
(gdyż iloczyny
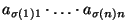 i
i
 różnią się tylko kolejnością czynników)
różnią się tylko kolejnością czynników)
(tu dokonujemy podstawienia
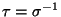 ; gdy
; gdy 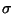 przebiega
przebiega
 ,
,  również przebiega
również przebiega  , ponadto
, ponadto
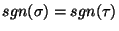 (uwaga 5.7))
(uwaga 5.7))
Z twierdzenia 5.14 wynika, że wszystkie własności wyznacznika
wyrażone w terminach kolumn macierzy są prawdziwe w terminach
wierszy.
Wniosek 5.15
Niech

będzie macierzą kwadratową. Wówczas kolumny macierzy

są liniowo niezależne
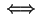
wiersze macierzy

są liniowo
niezależne.
Dowód. Wiersze macierzy  to kolumny macierzy
to kolumny macierzy  . Dlatego
. Dlatego
kolumny macierzy  są liniowo niezależne
są liniowo niezależne
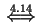 macierz
macierz  jest odwracalna
jest odwracalna
 kolumny macierzy
kolumny macierzy  są liniowo niezależne
są liniowo niezależne
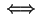 wiersze macierzy
wiersze macierzy  są liniowo niezależne.
są liniowo niezależne.
Wniosek 5.16
Załóżmy, że macierz kwadratowa

ma kolumny
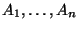
i
wiersze

.
1) Następujące operacje nie zmieniają
wyznacznika macierzy

.
a) Dodanie wektora
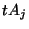
do
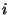
-tej kolumny (
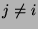
).
b) Dodanie wektora

do
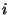
-tego wiersza (
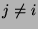
).
2) Zamiana wierszy (lub kolumn) miejscami zmienia znak wyznacznika.
3)
![$\det\left[\begin{array}{lllcl}a_{11}&a_{12}&a_{13}&\cdots&a_{1n}\\
0&a_{22}&a...
...
0&0&0&\dots&a_{nn}\end{array}\right]=a_{11}\cdot a_{22}\cdot\dots\cdot a_{nn}$](img823.png)
.
Dowód. (1) i (2) są łatwe. Dla dowodu (3) wykorzystamy wzór
 . W przypadku macierzy górnotrójkątnej występującej w
(3), iloczyn występujący we wzorze
. W przypadku macierzy górnotrójkątnej występującej w
(3), iloczyn występujący we wzorze  jako składnik sumy
dla permutacji
jako składnik sumy
dla permutacji 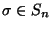 znika, gdy dla pewnego
znika, gdy dla pewnego  (gdyż wówczas w naszej macierzy
(gdyż wówczas w naszej macierzy
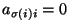 ). Zatem sumowanie
można ograniczyć do permutacji
). Zatem sumowanie
można ograniczyć do permutacji 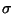 spełniających
spełniających
dla wszystkich  . łatwo jednak dowieść, że jedyną
taką permutacją jest permutacja
. łatwo jednak dowieść, że jedyną
taką permutacją jest permutacja 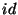 , dla której
, dla której 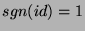 . Stąd
natychmiast wynika równość (3).
. Stąd
natychmiast wynika równość (3).



Next: 6. Wyznacznik, zmiana bazy
Up: Algebra liniowa II
Previous: 4. Przekształcenia liniowe i
Ludomir Newelski
2005-09-21
![]() są liniowo
niezależne
są liniowo
niezależne ![]()
![]() -wymiarowa objętość ``równoległościanu''
-wymiarowa objętość ``równoległościanu''
![]() jest
jest ![]() . Są wzory definiujące tę objętość, poznamy
je w rozdziale 15. Wygodniej jednak zdefiniować
. Są wzory definiujące tę objętość, poznamy
je w rozdziale 15. Wygodniej jednak zdefiniować ![]() -wymiarową
objętość ``zorientowaną'' ``równoległościanu''
-wymiarową
objętość ``zorientowaną'' ``równoległościanu'' ![]() (o
wartościach dodatnich lub ujemnych), równą
co do wartości bezwzględnej zwykłej
(o
wartościach dodatnich lub ujemnych), równą
co do wartości bezwzględnej zwykłej ![]() -wymiarowej
objętości. Rolę takiej zorientowanej objętości bedzie odgrywać
funkcja wyznacznika
-wymiarowej
objętości. Rolę takiej zorientowanej objętości bedzie odgrywać
funkcja wyznacznika
![]() . Mówiąc nieformalnie, powinno być
. Mówiąc nieformalnie, powinno być
![]() , następnie
udowodnimy, że istnieje dokładnie jedna funkcja o tych
własnościach. W rozdziale 15 udowodnimy, że tak określona funkcja
, następnie
udowodnimy, że istnieje dokładnie jedna funkcja o tych
własnościach. W rozdziale 15 udowodnimy, że tak określona funkcja
![]() w istocie spełnia
w istocie spełnia ![]() .
Macierze wymiaru
.
Macierze wymiaru ![]() będziemy tu zapisywać
jako układy
będziemy tu zapisywać
jako układy ![]() kolumn czy też wręcz układy
kolumn czy też wręcz układy ![]() wektorów z
wektorów z
![]() . Zatem
. Zatem ![]() możemy uważać za n-argumentową funkcję o
argumentach z
możemy uważać za n-argumentową funkcję o
argumentach z
![]() i wartościach w
i wartościach w ![]() .
.
![]() spelniająca D1-D4. Do tego celu będziemy potrzebować
pewnych wiadomości o permutacjach.
spelniająca D1-D4. Do tego celu będziemy potrzebować
pewnych wiadomości o permutacjach.
![]() permutacji
permutacji
![]() jest
również permutacją z
jest
również permutacją z ![]() . Składanie permutacji nazywamy też
mnożeniem permutacji i piszemy
. Składanie permutacji nazywamy też
mnożeniem permutacji i piszemy
![]() zamiast
zamiast
![]() . Na przykład
. Na przykład
![]() transpozycją
transpozycją ![]() nazywamy permutację
nazywamy permutację
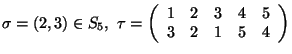 . Wówczas
. Wówczas
![]() jest również bijekcją, czyli
permutacją. Nazywamy ją permutacją odwrotną do permutacji
jest również bijekcją, czyli
permutacją. Nazywamy ją permutacją odwrotną do permutacji ![]() i oznaczamy przez
i oznaczamy przez ![]() . Mamy
. Mamy
![]() ,
dlatego odwracanie permutacji polega (w zapisie dwuwierszowym) na
zamianie miejscami wierszy górnego i dolnego:
,
dlatego odwracanie permutacji polega (w zapisie dwuwierszowym) na
zamianie miejscami wierszy górnego i dolnego:
 ,
,
![]() , czyli
, czyli
![]() będzie dowolne. Na mocy uwagi 5.2
będzie dowolne. Na mocy uwagi 5.2
![]() jest iloczynem transpozycji liczb sąsiednich:
jest iloczynem transpozycji liczb sąsiednich:
![]() . Zatem
. Zatem
![]() powstaje z
powstaje z
![]() przez
przez ![]() transpozycji kolumn sąsiednich, co zmienia znak
transpozycji kolumn sąsiednich, co zmienia znak ![]()
![]() -razy. Gdy
-razy. Gdy ![]() jest parzyste,
jest parzyste, ![]() . Gdy
. Gdy ![]() jest
nieparzyste,
jest
nieparzyste,
![]() . Stąd dostajemy (3).
. Stąd dostajemy (3).
![]() dla pewnych
dla pewnych ![]() . Niech
. Niech
![]() będzie permutacją taką, że
będzie permutacją taką, że ![]() i
i
![]() . Wówczas
. Wówczas
![]() ,
więc na mocy D3 i (3)
,
więc na mocy D3 i (3)
![]() .
.
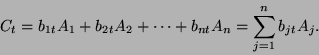
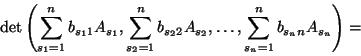

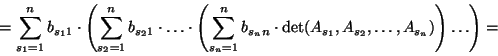
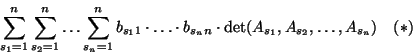
![]() definiujemy funkcję
definiujemy funkcję
![]() wzorem
wzorem ![]() . Zwróćmy uwagę, że
. Zwróćmy uwagę, że
![]() sumowanie możemy ograniczyć do tych układów
sumowanie możemy ograniczyć do tych układów
![]() , które odpowiadają permutacjom
, które odpowiadają permutacjom
![]() . Wówczas
. Wówczas
![]() . Przyjmując w twierdzeniu 5.9
. Przyjmując w twierdzeniu 5.9 ![]() dostajemy
następujący wniosek.
dostajemy
następujący wniosek.
![]() jest odwracalna
(znalezienie takiego kryterium było celem tego rozdziału).
jest odwracalna
(znalezienie takiego kryterium było celem tego rozdziału).

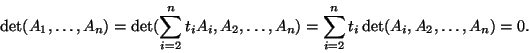
![]() Załóżmy, że
Załóżmy, że ![]() jest odwracalna. Wtedy istnieje macierz
odwrotna
jest odwracalna. Wtedy istnieje macierz
odwrotna ![]() taka, że
taka, że
![]() . Z twierdzenia
Cauchy'ego dostajemy
. Z twierdzenia
Cauchy'ego dostajemy
![]() , więc
, więc
![]() .
.
![]() .
.
![]() nazywamy macierz
nazywamy macierz
![]() , gdzie
, gdzie
![]() . Macierz
. Macierz ![]() nazywamy też macierzą transponowaną względem
nazywamy też macierzą transponowaną względem ![]() . Innymi słowy,
transpozycja polega na przestawieniu wierszy i kolumn danej macierzy.
Na przykład dla macierzy
. Innymi słowy,
transpozycja polega na przestawieniu wierszy i kolumn danej macierzy.
Na przykład dla macierzy
![$A=\left[\begin{array}{ccc}1&2&3\\
4&5&6\end{array}\right]$](img807.png) macierz transponowana ma postać
macierz transponowana ma postać
![\begin{displaymath}A^*=\left[\begin{array}{cc}1&4 2&5 3&6\end{array}\right].\end{displaymath}](img808.png)
![$\det\left[\begin{array}{lllcl}a_{11}&a_{12}&a_{13}&\cdots&a_{1n}\\
0&a_{22}&a...
...
0&0&0&\dots&a_{nn}\end{array}\right]=a_{11}\cdot a_{22}\cdot\dots\cdot a_{nn}$](img823.png) .
.