2. Liniowa niezależność

Niech $V$ będzie przestrzenią liniową. W poprzednim rozdziale widzieliśmy, że z każdą podprzestrzenią $W$ przestrzeni $V$ związana jest pewna nowa przestrzeń liniowa $V/W$. Zobaczymy teraz, jak tworzyć pewne inne przestrzenie liniowe z podprzestrzeni przestrzeni $V$. Załóżmy, że $V_1,V_2$ są podprzestrzeniami $V$.

Uwaga 2.1 (1)   Suma $V_1+V_2$ jest podprzestrzenią $V$.
(2) Przekrój $V_1\cap V_2$ jest podprzestrzenią $V$.
(3) Przekrój dowolnej liczby podprzestrzeni $V$ jest podprzestrzenią $V$.

Dowód. Dla przykładu udowodnimy punkt (1). W tym celu musimy sprawdzić, że zbiór $V_1+V_2$ jest zamknięty względem dodawania wektorów i mnożenia wektorów przez skalary. Sprawdźmy dodawanie. Niech $v,w\in V_1+V_2$. Znaczy to, że

$$v=v_1+v_2,\ w=w_1+w_2$$

dla pewnych $v_1,w_1\in V_1, v_2,w_2\in V_2$. Zatem

$$v+w=(v_1+w_1)+(v_2+w_2)\in V_1+V_2,$$

gdyż

$$v_1+w_1\in V_1\mbox{ i } v_2+w_2\in V_2$$

($V_1$ i $V_2$ są podprzestrzeniami). Widzimy więc, że zbiór $V_1+V_2$ jest zamknięty względem dodawania wektorów. Sprawdzenie zamkniętości względem mnożenia przez skalary, jak również dowody (2) i (3), pozostawiamy jako ćwiczenie.

Dla ilustracji punktu (2) w uwadze 2.1 rozważmy dwie płaszczyzny $\Pi_1,\Pi_2\subset {\mathbb{R}}^3$ zawierające $O$. Są to więc podprzestrzenie ${\mathbb{R}}^3$. Ich przekrój jest pewną prostą przechodzącą przez $O$, a więc również (zgodnie z 2.1(2)) podprzestrzenią ${\mathbb{R}}^3$.

Inną operacją tworzenia nowych przestrzeni liniowych jest operacja produktu przestrzeni liniowych. Mianowicie, załóżmy że $V,W$ są dwiema przestrzeniami liniowymi. Wówczas na produkcie kartezjańskim tych zbiorów

$$V\times W=\{\langle v,w\rangle:v\in V,w\in W\}$$

definiujemy działania dodawania wektorów i mnożenia wektorów przez skalar $t\in {\mathbb{R}}$ w następujący sposób.

$$\langle v,w\rangle+\langle v',w'\rangle=\langle v+v',w+w'\rangle$$

$$t\langle v,w\rangle=\langle tv,tw\rangle,$$

we wzorach tych $v+v'$ to suma wektorów $v,v'$ w przestrzeni $V$, $tv$ to skalarna krotność wektora $v$ w przestrzeni $V$, zaś $w+w',tw$ są obliczane w przestrzeni $W$.

Zbiór $V\times W$ z tak określonymi działaniami jest przestrzenią liniową zwaną produktem przestrzeni liniowych $V$ i $W$.

Rysunek 2.1: Produkt przestrzeni liniowych $V$ i $W$

Podobnie definiujemy produkt $V_1\times V_2\times\cdots\times V_n$ wiekszej ilości przestrzeni liniowych. W przypadku dowolnej rodziny $\{V_i,i\in I\}$ przestrzeni liniowych, odpowiedni produkt będzie to zwykły produkt kartezjański

$$\Pi_{i\in I}V_i=\{\langle v_i,i\in I\rangle:v_i\in V_i\}$$

z działaniami zdefiniowanymi po współrzędnych (analogicznie jak wyżej).

Liniowa zależność i liniowa niezależność wektorów to główne pojęcia algebry liniowej. Czytelnik spotkał sie już zapewne z pojęciem liniowej niezależności wektorów w przestrzeniach ${\mathbb{R}}^2$ i ${\mathbb{R}}^3$. W przypadku dowolnej przestrzeni liniowej definicja jest analogiczna.

Definicja 2.2   Wektory $v_1,\dots,v_n\in V$ są liniowo zależne wtedy i tylko wtedy, gdy jeden z nich jest liniową kombinacją pozostałych. W przeciwnym razie mówimy, że wektory te są liniowo niezależne.

Przyjmujemy też, że uklad złożony z jednego wektora zerowego $O$ jest liniowo zależny (gdyż $O$ jest kombinacją liniową 0 wektorów). Przyjmujemy, że układ 0 wektorów jest liniowo niezależny.

Przykłady.

1. Wektory $X,Y,Z\in {\mathbb{R}}^3$ są liniowo zależne wtedy i tylko wtedy, gdy $X,Y,Z$ leżą na pewnej płaszczyźnie przechodzącej przez $O$.

2. Dla wektora $v\in V$ układ wektorów $v,v$ jest liniowo zależny. Wektory $O,v$ są liniowo zależne (bo $O=0v$ jest liniową kombinacją wektora $v$).

3. Jedynym liniowo zależnym wektorem $v\in V$ jest wektor zerowy $O$.

Definicja liniowej niezależności może być trudna do zastosowania w konkretnych przypadkach. Następujący fakt dostarcza nam użytecznego kryterium do sprawdzania, czy dany układ wektorów jest liniowo niezależny.

Fakt 2.3   Wektory $v_1,\dots,v_n\in V$ są liniowo niezależne $\iff$

$$(*) (\forall t_1,\dots,t_n\in {\mathbb{R}})(t_1v_1+\cdots+t_nv_n=O\Rightarrow t_1=t_2=\cdots=t_n=0)$$

Dowód. $\Rightarrow$. Nie wprost. Załóżmy, że $v_1,\dots,v_n\in V$ są liniowo niezależne, dla pewnych $t_1,\dots,t_n\in {\mathbb{R}}$ mamy

(a)

$t_1v_1+\cdots+t_nv_n=O$

oraz któreś $t_i$ jest $\neq0$. Rozważmy przypadek, gdy $t_1\neq 0$ (pozostałe przypadki są analogiczne).

Przekształcając (a) dostajemy

(b)

$t_1v_1=-(t_2v_2+\cdots+t_nv_n)$.

Mnożąc wektory po obu stronach równości (b) przez skalar $\frac{1}{t_1}$ dostajemy równość:

$$v_1=(-\frac{t_2}{t_1})v_2+\cdots+(-\frac{t_n}{t_1})v_n,$$

która pokazuje, że wektor $v_1$ jest liniową kombinacją wektorów $v_2,\dots,v_n$, co przeczy ich liniowej niezależności.

$\Leftarrow$. Nie wprost. Załóżmy, że wektory $v_1,\dots,v_n\in V$ spełniają warunek $(*)$, lecz są liniowo zależne, tzn. jeden z nich jest liniową kombinacją pozostałych. Rozpatrzymy przypadek, gdy $v_1$ jest liniową kombinacją wektorów $v_2,\dots,v_n$ (pozostałe przypadki są analogiczne). Znaczy to, że

$$v_1=t_2v_2+\cdots+t_nv_n$$

dla pewnych $t_2,\dots,t_n\in {\mathbb{R}}$. Równość ta implikuje, że

$$(-1)v_1+t_2v_2+\cdots+t_nv_n=O,$$

zatem warunek $(*)$ nie zachodzi dla skalarów $t_1=-1,t_2,\dots,t_n$, sprzeczność.

Przykłady.

1. Wektory bazowe $E_1,\dots,E_n\in {\mathbb{R}}^n$ są liniowo niezależne. By się o tym przekonać, sprawdzamy warunek $(*)$ z faktu 2.3. Przypuśćmy, że dla pewnych $t_1,\dots,t_n\in {\mathbb{R}}, t_1E_1+\cdots+t_nE_n=O$. Wektor $t_1E_1+\cdots+t_nE_n$ jest równy po prostu wektorowi

$$\left[\begin{array}{l}t_1 t_2 \vdots t_n\end{array}\right].$$

Zatem wszystkie skalary $t_1,\dots,t_n$ są równe $0$.

2. Podobnie sprawdzamy, że w przestrzeni wielomianów ${\mathbb{R}}[X]$ wektory $1,X,X^2,\dots,X^n$ są liniowo niezależne.

Definicja 1.2 dotyczy skończonego układu wektorów. Rozszerzymy ją obecnie podając definicje liniowej niezależności dla dowolnego zbioru wektorów w przestrzeni $V$.

Definicja 2.4   Załóżmy, że $A\subset V$.
1) Zbiór $A$ jest liniowo niezależny $\iff$ żaden wektor $v\in A$ nie jest liniową kombinacją wektorów ze zbioru $A\setminus\{v\}$.
2) Zbiór $A$ generuje $V\iff$ każdy wektor $v\in V$ jest liniową kombinacją wektorów z $A$ (tzn. $Lin(A)=V$). Mówimy też wtedy, że $A$ jest zbiorem generatorów przestrzeni $V$.
3) Ogólniej, dla podprzestrzeni $W\subset V$ mówimy, że $A$ generuje $W\iff Lin(A)=W$.
4) $A$ jest bazą przestrzeni $V\iff A$ jest liniowo niezależny i generuje $V$.

W szczególności cała przestrzeń $V$ generuje $V$.

Przykłady.

1. Gdy $V$ jest przestrzenią zerową, to zbiór $A=\emptyset$ generuje $V$ (bo $Lin(\emptyset)=\{O\}$) i jest liniowo niezależny, więc zbiór pusty jest bazą $V$.

2. Wektory $E_1,\dots,E_n\in R^n$ tworzą bazę przestrzeni ${\mathbb{R}}^n$. Ich liniowa niezależność była pokazana powyżej. Jasne jest też, że generują one ${\mathbb{R}}^n$.

3. Dowolny układ 3 liniowo niezależnych wektorów w ${\mathbb{R}}^3$ jest bazą ${\mathbb{R}}^3$. W istocie, przypuśćmy, że $X_1,X_2,X_3\in {\mathbb{R}}^3$ są liniowo niezależne. Wówczas ${\mathbb{R}}^3=\{t_1X_1+t_2X_2+t_3X_3:t_1,t_2,t_3\in {\mathbb{R}}\}$, więc wektory te generują ${\mathbb{R}}^3$. Podobnie pokazujemy, że każda para $X,Y\in {\mathbb{R}}^2$ wektorów liniowo niezależnych jest bazą ${\mathbb{R}}^2$.

4. Zbiór $\{1,X,X^2,X^3,\dots\}$ jest nieskończoną bazą przestrzeni ${\mathbb{R}}[X]$. Istotnie, sprawdzenie liniowej niezależności jest łatwe, podobne jak w przykładzie 2 po fakcie 2.3. By pokazać, że wektory te generują całą przestrzeń ${\mathbb{R}}[X]$ rozważmy dowolny wielomian $W(X)=a_0+a_1X+\cdots+a_kX_k$ o wyrazach rzeczywistych. Wówczas

$$W=a_0\cdot 1+a_1\cdot X+\cdots+a_k\cdot X^k,$$

tzn. $W$ jest liniową kombinacją wektorów $1,X,X^2,\dots,X^k$ ze skalarnymi współczynnikami $a_0,a_1,\dots,a_k$.

5. Czy wektory $1+X+X^2, 2+X, X+2X^2\in {\mathbb{R}}[X]$ są liniowo zależne ? By odpowiedzieć na to pytanie, stosujemy kryterium z faktu 2.3. Na mocy tego kryterium wektory te są liniowo zależne wtedy i tylko wtedy, gdy dla pewnych $t_1,t_2,t_3\in {\mathbb{R}}$ (nie wszystkich $=0$) mamy

(a)

$t_1(1+X+X^2)+t_2(2+X)+t_3(X+2X^2)=O$.

(a) jest równoważne temu, że wielomian

$$(t_1+2t_2)+(t_1+t_2+t_3)X+(t_1+2t_3)X^2$$

jest zerowy, to znaczy mamy

$$\left\{\begin{array}{rrrrrrr}t_1&+&2t_2&\mbox{}&\mbox{}&=&0\\... ...&+&t_3&=&0\\ t_1&+&\mbox{}&\mbox{}&2t_3&=&0\end{array}\right.$$

Powyższy układ równań ma niezerowe rozwiązanie, np. $t_1=2,t_2=t_3=1$, zatem wektory $1+X+X^2,2+X,X+2X^2$ są liniowo zależne.

W powyższych przykładach wskazaliśmy bazy niektórych przestrzeni liniowych. Okazuje się, że każda przestrzeń liniowa ma bazę.

Twierdzenie 2.5 (o istnieniu bazy)   1) Każdy zbiór liniowo niezależny $A\subset V$ można rozszerzyć do bazy przestrzeni $V$.
2) Każdy zbiór generatorów przestrzeni $V$ zawiera bazę.

Dowód. Dowód (1) przeprowadzimy w przypadku, gdy istnieje skończony zbiór generatorów $Y=\{y_1,\dots,y_k\}$ przestrzeni $V$ (w ogólnym przypadku rozumowanie jest podobne, zamiast skończonego zbioru $Y$ można wziąć jako zbiór generatorów całą przestrzeń $V$ i skorzystać w dowodzie z lematu Zorna).

Niech $Y'$ będzie maksymalnym podzbiorem $Y$ takim, że zbiór $A\cup Y'$ jest liniowo niezależny (w szczególnym przypadku może być nawet $Y'=\emptyset$). Pokażemy, że zbiór $A\cup Y'$ jest bazą przestrzeni $V$, w tym celu wystarczy tylko sprawdzić, że generuje $V$.

Po pierwsze sprawdzimy, że dowolny wektor $y\in Y$ jest liniową kombinacją wektorów z $A\cup Y'$. Jest to oczywiste, gdy $y\in Y'$. Gdy $y\not\in Y'$, to na mocy maksymalności zbioru $Y'$ dostajemy, że zbiór $A\cup Y'\cup\{y\}$ jest liniowo zależny. Na mocy faktu 2.3 i definicji 2.4 pewna liniowa kombinacja wektorów z $A\cup Y'\cup\{y\}$ (o nie wszystkich skalarnych współczynnikach $=0$) równa się wektorowi zerowemu, tzn.

(a)

$\sum t_ix_i+\sum r_jy'_j+sy=O$

dla pewnych $x_i\in A, y'_j\in Y'$ oraz $t_i,r_j,s\in {\mathbb{R}}$ nie wszystkich $=0$.

Gdyby $s$ było równe $0$, to kombinacja (a) byłaby kombinacją liniową wektorów z $A\cup Y'$, przecząc liniowej niezależności zbioru $A\cup Y'$. Dlatego $s\neq0$. Przekształcając (a) dostajemy

$$y=-\frac{1}{s}\left(\sum t_ix_i+\sum r_jy'_j\right),$$

widzimy więc, że $y$ jest liniową kombinacją wektorów z $A\cup Y'$.

Dowod (1) zakończymy pokazując, że dowolny wektor $v\in V$ jest liniową kombinacją wektorów z $A\cup Y'$. Wiemy, że $Y$ generuje $V$, więc $v$ jest liniową kombinacją

(b)

$v=\sum_{t=1}^ks_ty_t$

wektorów z $Y$. Wiemy też, że każdy wektor $y_t$ jest liniową kombinacją wektorów z $A\cup Y'$: $y_t=\sum_i r_{t,i}v_{t,i}$ dla pewnych $v_{t,i}\in A\cup Y'$ oraz $r_{t,i}\in {\mathbb{R}}$. Podstawiając w (b) za $y_t$ te liniowe kombinacje dostajemy

$$v=\sum_{t=1}^ks_t(\sum_ir_{t,i}v_{t,i})=\sum_{t,i}s_tr_{t,i}v_{t,i}.$$

Widzimy więc, że wektor $v$ też jest liniową kombinacją wektorów z $A\cup Y'$.

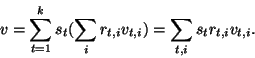
(2) Ten sam dowód, dla $A=\emptyset$.

Wniosek 2.6   Każda przestrzeń liniowa ma bazę.

Znaczenie pojęcia bazy wynika z następującego twierdzenia Steinitza.

Twierdzenie 2.7   Każde dwie bazy przestrzeni $V$ są równoliczne.

Dowód. Dowód przeprowadzimy w przypadku, gdy pewna baza $V$ jest skończona (ogólny przypadek wymaga pewnego rachunku na liczbach kardynalnych). Przypuśćmy więc, że ${\cal A},{\cal B}$ są dwiema bazami przestrzeni $V$, przy czym ${\cal A}=\{a_1,\dots,a_k\}$ jest skończona. Pokażemy, że bazy te są równoliczne.

Najpierw pokażemy, że ${\cal B}$ ma $\leq k$ elementów. Przypuśćmy nie wprost, że $\vert{\cal B}\vert>k$. Wybierzmy różne wektory $b_1,\dots,b_{k+1}\in {\cal B}$.

Niech $X={\cal A}$. Idea dowodu polega na stopniowym zastępowaniu w zbiorze $X$ wektorów ze zbioru ${\cal A}$ przez wektory ze zbioru ${\cal B}$ tak jednak, że zbiór $X$ pozostaje cały czas zbiorem generatorów przestrzeni $V$.

Rozważmy najpierw wektor $b_1\in {\cal B}$. Możemy go przedstawić w postaci liniowej kombinacji wektorów ze zbioru $X={\cal A}$:

$$b_1=t_{1,1}a_1+\cdots+t_{1,k}a_k.$$

Nie wszystkie $t_{1,i}$ są $=0$ (bo $b_1\neq O$). Przenumerowując w razie potrzeby wektory $a_1,\dots,a_k$ możemy założyć, że $t_{1,k}\neq 0$. Stąd dostajemy

$$a_k=\frac{1}{t_{1,k}}b_1+(-\frac{t_{1,1}}{t_{1,k}})a_1+\cdots... ...frac{t_{1,k-1}}{t_{1,k}})a_{k-1}\in Lin(b_1,a_1,\dots,a_{k-1}).$$

Zatem $X\subset Lin(b_1,a_1,\dots,a_{k-1})$, więc skoro $X$ generuje $V$, to również $\{b_1,a_1,\dots,a_{k-1}\}$ generuje $V$. Zastępujemy zatem w zbiorze $X$ wektor $a_k$ przez wektor $b_1$.

Rozważmy teraz kolejny wektor $b_2\in {\cal B}$. Możemy go znów przedstawić jako liniową kombinację wektorów z $X$.

$$b_2=s_{2,1}b_1+t_{2,1}a_1+\cdots+t_{2,k-1}a_{k-1},$$

przy czym nie wszystkie $s_{2,1},t_{2,i}$ są $=0$. Jeśliby wszystkie $t_{2,i}$ były równe $0$, to $b_1,b_2$ byłyby liniowo zależne, sprzeczność. Dlatego pewne $t_{2,i}\neq 0$. Zmieniając numerację wektorów $a_i$ możemy założyć, że $t_{2,k-1}\neq 0$.

Stąd podobnie jak wyżej mamy $a_{k-1}\in Lin(b_1,b_2,a_1,\dots,a_{k-2})$, więc $V=Lin(b_1,b_2,a_1,\dots,a_{k-2})$, i możemy w zbiorze $X$ zastąpić wektor $a_{k-1}$ przez wektor $b_2$.

Po $k$ krokach wyrzucimy w ten sposób ze zbioru $X$ wszystkie wektory $a_i$ i zbiór ten będzie miał postać $X=\{b_1,b_2,\dots,b_k\}$. Będzie to nadal zbiór generatórów $V$. W szczególności wektor $b_{k+1}$ będzie liniową kombinacją wektorów $b_1,\dots,b_k$, przecząc liniowej niezależności bazy ${\cal B}$.

W ten sposób pokazaliśmy, że $\vert{\cal B}\vert\leq\vert{\cal A}\vert$. Odwracając rolami ${\cal A}$ i ${\cal B}$ w powyższym dowodzie dostajemy $\vert{\cal A}\vert\leq \vert{\cal B}\vert$. Dlatego ${\cal A}$ i ${\cal B}$ są równoliczne.

Definicja 2.8   Liczbę elementów dowolnej bazy przestrzeni $V$ nazywamy wymiarem przestrzeni $V$. Wymiar $V$ oznaczamy przez $\dim(V)$. W przypadku, gdy liczba ta jest nieskończona, możemy napisać $\dim(V)=\infty$.

Przykłady.

1. $\dim({\mathbb{R}}^n)=n$. Istotnie, bazą jest tu zbiór $n$-elementowy $\{E_1,\dots,E_n\}$, zwany bazą standardową przestrzeni ${\mathbb{R}}^n$. Bazę tę oznaczamy symbolem $\cal E$. W szczególności $\dim({\mathbb{R}})=\dim({\mathbb{R}}^1)=1$, bazą ${\mathbb{R}}$ jest dowolna liczba niezerowa.

2. $\dim({\mathbb{R}}[X])=\infty$. Bazą standardową jest tu zbiór wektorów
$\{1,X,X^2,X^3,\dots\}$.

3. Przestrzeń liniowa ma zazwyczaj wiele baz (porównaj przykłady po definicji 2.4).

W poniższej uwadze wyliczamy podstawowe własności wymiaru.

Uwaga 2.9   Niech $V_1,V_2$ będą podprzestrzeniami $V$.
1) $\dim(V_1)\leq\dim(V)$.
2) $\dim(V_1)=\dim(V)<\infty\Rightarrow V_1=V$.
3) (modularność) $\dim(V_1+V_2)=\dim(V_1)+\dim(V_2)-\dim(V_1\cap V_2)$.

Dowód. (1),(2). Stosując twierdzenie 2.5 znajdujemy dwie bazy ${\cal B}$ (przestrzeni $V_1$) i ${\cal B}'$ (przestrzeni $V$) takie, że ${\cal B}\subset {\cal B}'$. Jasne, że $\vert{\cal B}\vert\leq\vert{\cal B}'\vert$, czyli $\dim(V_1)\leq\dim(V)$. Jeśli $dim(V_1)=\dim(V)<\infty$, to $\vert{\cal B}\vert=\vert{\cal B}'\vert$, więc ${\cal B}={\cal B}'$ i $V_1=Lin({\cal B})=V$.

Dowód (3) pozostawiamy jako zadanie.