UNIVERSITY
OF WROC£AW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
43.1 42.2 42.1 41.2 41.1 40.2 40.1
39.2 39.1 38.2 38.1 37.2 37.1 36.2
36.1 35.2 35.1 34.2 34.1 33.2 33.1
32.2 32.1 31.2 31.1 30.2 30.1 29.2
29.1 28.2 28.1 27.2 27.1 26.2 26.1
25.2 25.1 24.2 24.1 23.2 23.1 22.2
22.1 21.2 21.1 20.2 20.1 19.2 19.1
18.2 18.1 17.2 17.1 16.2 16.1 15
14.2 14.1 13.2 13.1 12.2 12.1 11.2
11.1 10.2 10.1 9.2 9.1 8 7.2
7.1 6.2 6.1 5.2 5.1 4.2 4.1
3.2 3.1 2.2 2.1 1.2 1.1
 
 
WROC£AW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 33, Fasc. 2,
pages 363 - 375
 

ON FREE INFINITE DIVISIBILITY FOR CLASSICAL MEIXNER DISTRIBUTIONS

Marek Bożejko
Takahiro Hasebe

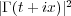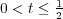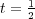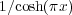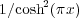Abstract: We prove that symmetric Meixner distributions, whose probability densities are proportional to |Γ (t+ ix)|2 , are freely infinitely divisible for 0 < t ≤ 1 2 . The case t = 1 2 corresponds to the law of Lévy’s stochastic area whose probability density is 1∕cosh (πx ) . A logistic distribution, whose probability density is proportional to 1∕cosh2(πx) , is also freely infinitely divisible.

2000 AMS Mathematics Subject Classification: Primary: 46L54; Secondary: 30C45.

Keywords and phrases: Meixner distribution, Lévy’s stochastic area, logistic distribution, free infinite divisibility.

Download:    Abstract    Full text   Abstract + References