TANAKA FORMULA FOR STRICTLY STABLE PROCESSES
Abstract: For symmetric Lévy processes, if the local times exist, the Tanaka formula has already
been constructed via the techniques in the potential theory by Salminen and Yor (2007). In
this paper, we study the Tanaka formula for arbitrary strictly stable processes with index
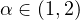 , including spectrally positive and negative cases in a framework of Itô’s
stochastic calculus. Our approach to the existence of local times for such processes is
different from that of Bertoin (1996).
, including spectrally positive and negative cases in a framework of Itô’s
stochastic calculus. Our approach to the existence of local times for such processes is
different from that of Bertoin (1996).
2000 AMS Mathematics Subject Classification: Primary: 60J55; Secondary:
60G52.
Keywords and phrases: Local time, stable process, Itô’s stochastic calculus.