STRONG LAWS OF LARGE NUMBERS FOR THE SEQUENCE OF THE
MAXIMUM OF PARTIAL SUMS OF I.I.D. RANDOM VARIABLES
Shuhua Chang
Deli Li
Andrew Rosalsky
Abstract: Let 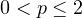 , let
, let 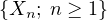 be a sequence of independent copies of a
real-valued random variable
be a sequence of independent copies of a
real-valued random variable 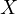 , and set
, and set 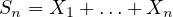 ,
, 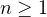 . Motivated by a
theorem of Mikosch (1984), this note is devoted to establishing a strong law of large numbers
for the sequence
. Motivated by a
theorem of Mikosch (1984), this note is devoted to establishing a strong law of large numbers
for the sequence 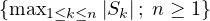 . More specifically, necessary and sufficient
conditions are given for
. More specifically, necessary and sufficient
conditions are given for
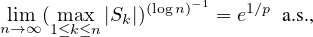
where 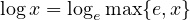 ,
, 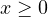 .
.
2000 AMS Mathematics Subject Classification: Primary: 60F15; Secondary: 60G50,
60G70.
Keywords and phrases: Theorem of Mikosch, i.i.d. real-valued random variables,
maximum of partial sums, strong law of large numbers.