ON THE LONGEST RUNS IN MARKOV CHAINS
Zhenxia Liu
Xiangfeng Yang
Abstract: In the first 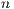 steps of a two-state (success and failure) Markov chain, the longest
success run
steps of a two-state (success and failure) Markov chain, the longest
success run 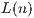 has been attracting considerable attention due to its various applications.
In this paper, we study
has been attracting considerable attention due to its various applications.
In this paper, we study 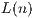 in terms of its two closely connected properties: moment
generating function and large deviations. This study generalizes several existing results in
the literature, and also finds an application in statistical inference. Our method on
the moment generating function is based on a global estimate of the cumulative
distribution function of
in terms of its two closely connected properties: moment
generating function and large deviations. This study generalizes several existing results in
the literature, and also finds an application in statistical inference. Our method on
the moment generating function is based on a global estimate of the cumulative
distribution function of 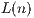 proposed in this paper, and the proofs of the large
deviations include the Gärtner–Ellis theorem and the moment generating function.
proposed in this paper, and the proofs of the large
deviations include the Gärtner–Ellis theorem and the moment generating function.
2010 AMS Mathematics Subject Classification: Primary: 60F10, 44A1; Secondary:
60J10, 60G70.
Keywords and phrases: Longest run, moment generating function, large deviation
principle, Markov chain.