LIMITING SPECTRAL DISTRIBUTIONS OF SUMS OF PRODUCTS OF
NON-HERMITIAN RANDOM MATRICES
Holger Kösters
Alexander Tikhomirov
Abstract: For fixed 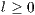 and
and 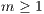 , let
, let 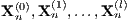 be independent random
be independent random 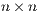 matrices with independent entries, let
matrices with independent entries, let 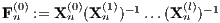 , and let
, and let
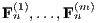 be independent random matrices of the same form as
be independent random matrices of the same form as 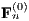 . We show that as
. We show that as
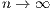 , the matrices
, the matrices 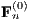 and
and 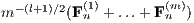 have the same limiting
eigenvalue distribution.
have the same limiting
eigenvalue distribution.
To obtain our results, we apply the general framework recently introduced in Götze,
Kösters, and Tikhomirov (2015) to sums of products of independent random matrices and
their inverses. We establish the universality of the limiting singular value and eigenvalue
distributions, and we provide a closer description of the limiting distributions in terms of free
probability theory.
2010 AMS Mathematics Subject Classification: Primary: 60B20; Secondary: 60E07,
60F05, 46L54.
Keywords and phrases: Non-Hermitian random matrices, limiting spectral distributions,
free probability theory, stable distributions.