SERIES REPRESENTATION OF TIME-STABLE STOCHASTIC PROCESSES
Christoph Kopp
Ilya Molchanov
Abstract: A stochastically continuous process 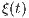 ,
, 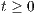 , is said to be time-stable if the sum
of
, is said to be time-stable if the sum
of 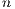 i.i.d. copies of
i.i.d. copies of 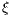 equals in distribution the time-scaled stochastic process
equals in distribution the time-scaled stochastic process 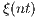 ,
,
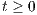 . The paper advances the understanding of time-stable processes by means of their
LePage series representations as the sum of i.i.d. processes with the arguments scaled by the
sequence of successive points of the unit intensity Poisson process on
. The paper advances the understanding of time-stable processes by means of their
LePage series representations as the sum of i.i.d. processes with the arguments scaled by the
sequence of successive points of the unit intensity Poisson process on 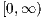 . These series
yield numerous examples of stochastic processes that share one-dimensional distributions
with a Lévy process.
. These series
yield numerous examples of stochastic processes that share one-dimensional distributions
with a Lévy process.
2010 AMS Mathematics Subject Classification: Primary: 60G52; Secondary:
60G51.
Keywords and phrases: Infinite divisibility, LePage series, Lévy process, point process,
time-stable process.