G. Jagiella

Skrypt do wykładu Programowanie 2 (Python)

ostatnia modyfikacja: 13.07.2021

Wykład 5 (cz. 1) - algorytmy sortujące I

Spis treści

Wstęp

Zagadnienie sortowania

Klasycznym zagadnieniem w informatyce jest problem sortowania ciągu parami porównywalnych obiektów (np. liczb). W tym rozdziale opiszemy kilka podstawowych algorytmów sortowania, oraz co je rozróżnia.

Na początku ustalimy pewne kwestie formalne.

  • Obiekty porównujemy według pewnego ustalonego praporządku. Przypomnienie: praporządek to relacja, która spełnia dwa z aksjomatów porządku częściowego (jest zwrotna i przechodnia), ale niekoniecznie jest słabo antysymetryczna. Przykładem takiego praporządku jest relacja $\preceq$ na zbiorze osób $S$, gdzie dla osób $a, b \in S$ deklarujemy, że $a \preceq b \iff \text{nazwisko }a \text{ jest alfabetycznie wcześniej, niż nazwisko }b$.
  • Gdy $\preceq$ jest praporządkiem, powiemy że ciąg $a_0, a_1, \ldots, a_{n-1}$ jest posortowany (uporządkowany), gdy $(\forall 0 \leq i \leq j < n) ~ a_i \preceq a_j$.
  • Obiekty które sortujemy będą elementami listy. W konsekwencji, odczyt lub zastąpienie elementu ciągu będzie się odbywać w stałym czasie. Długość ciągu będzie znana. Obiekty na liście mogą się powtarzać.

Matematycznie: niech $a_0, a_1, \ldots, a_{n-1}$ będzie ciągiem obiektów porównywalnych praporządkiem $\preceq$. Posortowaniem danego ciągu jest taki ciąg $a_{\sigma(0)}, a_{\sigma(1)}, \ldots, a_{\sigma(n-1)}$ (gdzie $\sigma \colon \{0, \ldots, n-1\} \to \{0, \ldots, n-1\}$ jest permutacją), że $a_{\sigma(i)} \preceq a_{\sigma(j)}$ dla wszystkich $0 \leq i \leq j < n$.

Bardziej programistycznie:
Wejściem algorytmu sortującego będzie zatem lista parami porównywalnych obiektów, a oczekiwanym wyjściem taka jej permutacja, która jest posortowana.

Różnice między algorytmami sortującymi

Istnieje wiele algorytmów sortujących daną listę obiektów. Nie ma wsród nich uniwersalnego i optymalnego dla każdej sytuacji. Wskażemy teraz pewne cechy, które pozwolą nam na porównanie poznawanych algorytmów.

  • Zastosowania. Wiele algorytmów sortujące służy do ogólnego zastosowania: mogą służyć do sortowania obiektów dowolnych typów. Niektóre algorytmy są jednak zaprojektowane z myślą o konkretnych obiektach, np. liczbach1.
  • Złożoność czasowa. Czas pracy algorytmów jest głównym kryterium ich wydajności. W algorytmach sortujących dominującymi operacjami są porównania oraz zamiana elementów na liście. W Pythonie, zamiana elementów na liście to (zazwyczaj) bardzo prosta operacja, jednak porównanie dwóch obiektów może być wymagającym zadaniem2. Rozmiarem danych algorytmu sortującego jest prawie zawsze rozmiar listy do posortowania.
  • Złożoność pamięciowa. Ta złożoność to, obok złożoności czasowej, inna miara efektywności wykorzystania zasobów przez algorytm (niekoniecznie algorytm sortujący). U nas będzie oznaczać dodatkową ilość pamięci potrzebną algorytmowi na zrealizowanie zadania. Ta dodatkowa pamięć wyraża się jako funkcja rozmiaru danych. Do opisu tej funkcji stosuje się notację asymptotyczną, tak jak w przypadku złożoności czasowej3.
  • Stabilność sortowania. Pojęcie stabilności opiszemy w następnym podrozdziale. Algorytm sortujący może sortować listę w sposób stabilny lub niestabilny.
  • Inne powody. Powyższa lista nie jest w żadnym wypadku wyczerpująca: o przydatności algorytmu (dowolnego) decydują też szczególne przypadki zastosowań, łatwość implementacji, wydajność dla małych rozmiarów danych (niezależnie od złożoności asymptotycznej), skalowalność (łatwość rozłożenia operacji na wiele procesorów), etc.

Przypisy:
1: W tym skrypcie omówimy jedynie algorytmy zastosowań ogólnych.
2: Takie porównanie może być realizowane dowolnie skomplikowanym algorytmem. Przykładami są porównania dwóch napisów długości $n$ (czas $O(n)$) oraz porównanie dwóch macierzy rozmiaru $n \times n$ względem ich odległości euklidesowej od macierzy zerowej (czas $\Theta(n^2)$).
3: Dzięki temu można na przykład powiedzieć, że "algorytm wymaga stałej ilości dodtkowej pamięci", lub "pesymistycznie, algorytm wymaga kwadratowej ilości pamięci", etc.

Stabilność

Gdy $\preceq$ jest praporządkiem, o obiektach $a, b$ takich, że $a \preceq b$ i $b \preceq a$ będziemy mówić, że są równe (w sensie praporządku). Na liście obiektów do posortowania mogą wystąpić różne, ale równe w sensie praporządku elementy, np. dwie takie same liczby. Algorytm, sortując listę, może umieścić je w posortowanej liście w dowolnej kolejności. Nie będzie to miało znaczenia dla wyniku: liczby są od siebie nieodróżnialne.

Z drugiej strony jednak, na liście mogą pojawić się obiekty, które są równe według praporządku, ale nie są ze sobą tożsame. Przykładem jest lista osób (imię oraz nazwisko), porządkowana według nazwisk - i tylko nazwisk. Przykładowo, dana jest lista:
['Anna Kowalska' , 'Marek Nowak' , 'Zuzanna Kowalska']
Elementy 'Anna Kowalska' i 'Zuzanna Kowalska' są równe w sensie porządku. Lista może zatem zostać posortowana na dwa sposoby:

  1. ['Anna Kowalska', 'Zuzanna Kowalska', 'Marek Nowak']
  2. ['Zuzanna Kowalska', 'Anna Kowalska', 'Marek Nowak']

Obie powyższe listy są posortowane. Różnią się jednak tym, że w pierwszej z nich elementy 'Anna Kowalska' i 'Zuzanna Kowalska' występują w takiej samej kolejności, jak w oryginalnej liście, a w drugiej ich kolejność jest zamieniona. Pytanie, czy sortowanie zachowuje kolejność równych (według praporządku) elementów czy nie prowadzi do następującej definicji:

Definicja. Niech $a_0, a_1, \ldots, a_{n-1}$ będzie ciągiem obiektów. Niech $\sigma \colon \{0, \ldots, n-1\} \to \{0, \ldots, n-1\}$ będzie permutacją taką, że ciąg $a_{\sigma(0)}, a_{\sigma(1)}, \ldots, a_{\sigma(n-1)}$ jest posortowany. Powiemy, że ciąg ten jest posortowany stabilnie wtedy, gdy dla wszystkich $i \leq j$ takich, że $a_i$ i $a_j$ są równe w sensie porządku zachodzi $\sigma(i) \leq \sigma(j)$.

Wniosek. Istnieje dokładnie jeden sposób stabilnego posortowania ciągu.

W przykładzie wyżej, lista 1. jest efektem stabilnego posortowania listy wejściowej.

Pokażemy przykład, w którym sortowanie stabilne jest przydatne. Rozważmy listę osób, którą chcemy posortować względem nazwisk, a potem imion. Jednym ze sposobów jest posortowanie ich ze względu na leksykograficzny (pra)porządek na parach (nazwisko, imię). Nie zawsze jest to możliwe: osoby mogą być zapisane np. jako wiersze w arkuszu kalkulacyjnym, w których jedna kolumna zawiera imię, a drugie nazwisko, a sortować wolno nam tylko według jednej kolumny. W tej sytuacji, możemy wykonać następujące kroki:

  1. Najpierw posortować osoby po imionach (sic).
  2. Następnie posortować tak posortowaną listę po nazwiskach w sposób stabilny.

Krok 1. gwarantuje nam, że na liście, którą sortujemy w kroku 2., osoby o wcześniejszych (wg słownika) imionach występują przed osobami o imionach późniejszych. Po posortowaniu listy w sposób stabilny, osoby współdzielące nazwisko wciąż będą występowały w kolejności imion. Przykładowa lista, do której zaaplikowano kroki 1. i 2.:

                Anna Nowak               Adam Nowak               Anna Kowalska
                Maria Nowak              Anna Nowak               Maria Kowalska
                Zuzanna Kowalska         Anna Kowalska            Zuzanna Kowalska
                Marek Nowak         1    Anna Wójcik         2    Adam Nowak
                Maria Kowalska    ---->  Marek Nowak       ---->  Anna Nowak
                Adam Nowak               Marek Wójcik             Marek Nowak
                Marek Wójcik             Maria Nowak              Maria Nowak
                Anna Kowalska            Maria Kowalska           Anna Wójcik
                Anna Wójcik              Zuzanna Kowalska         Marek Wójcik
Uwaga. Algorytm sortujący niestabilnie może zostać wykorzystany do zasymulowania algorytmu sortującego stabilnie: zamiast sortować oryginalny ciąg $a_0, a_1,\ldots,a_{n-1}$, można posortować leksykograficznie ciąg par, w którym każdy element ciągu występuje wraz ze swoim indeksem, czyli ciąg $(a_0, 0), (a_1, 1),\ldots,(a_{n-1},n-1)$. Ten zabieg sprawia, że żadna para obiektów do posortowania nie jest równa według praporządku (zatem jest to prawdziwy porządek). Jeśli dla $i < j$ elementy $a_i$ i $a_j$ są równe według (oryginalnego) praporządku, wtedy porównanie par $(a_i, i)$ i $(a_j, j)$ jest rozstrzygane przez drugą współrzędną, wobec czego $(a_i, i) < (a_j, j)$. Zauważmy jednak, że algorytm działający w ten sposób musi skonstruować listę takich par.

Przegląd podstawowych algorytmów

W najbliższych rozdziałach omówimy następujące algorytmy ogólnego zastosowania:

  1. Selection sort (sortowanie przez wybieranie),
  2. Insertion sort (sortowanie przez wstawianie),
  3. Merge sort (sortowanie przez scalanie),
  4. Quicksort (sortowanie szybkie).

Oprócz tego, krótko omówimy tzw. algorytmy hybrydowe, polegające na połączeniu dwóch lub więcej algorytmów, w szczególności (uproszczony wariant) algorytmu Timsort (wykorzystywanego w bibliotece Pythona i implementującego metodę sort() dla wbudowanych list), oraz warianty Introsort (typową implementację funkcji sortującej z biblioteki standardowej C++).

Lista oczywiście nie jest wyczerpująca. Pominiemy część klasycznych algorytmów (np. ShellSort, Heapsort), oraz wiele algorytmów do zastosowań szczególnych: Radix sort, Bucket sort, Counting sort, ...

Opisując algorytmy, będziemy przynajmniej częściowo uzasadniać ich poprawność. Do tego celu wprowadzimy w tym rozdziale jeszcze jedno pojęcie.

Niezmiennik pętli

Niezmiennik pętli (loop invariant) to własność zachowana na początku (końcu) każdej iteracji (obrotu) danej pętli. Własności te nazwiemy (zgodnie z tradycyjną terminologią) warunkami PRE i POST (odpowiednio początek i koniec pętli). Warunki te definiujemy w zależności od numeru (lub inaczej określonego kroku) iteracji.

Niezmiennik pętli jest jednym z fundamentalnych sposobów dowodzenia poprawności algorytmów. Jako ilustrację, rozważmy typową implementację algorytmu wyliczającego iteracyjnie $n$-tą liczbę ciągu Fibonacciego, którego poprawność udowodnimy w formalny sposób:

def fib(n):
    a, b = 0, 1
    for i in range(n):
        a, b = b, a + b
    return a

Zmienną w pętli for oznaczyliśmy przez i; będziemy odnosić się przez nią do numeru obrotu pętli: iteracja zerowa, pierwsza, ..., (n - 1)-wsza. Oznaczmy i-ty wyraz ciągu Fibonacciego przez $f_i$. Określmy warunki PRE i POST dla i-tej iteracji następująco:

  • PRE(i) (warunek na początku i-tego obrotu pętli): a i b są równe odpowiednio $f_i$ i $f_{i+1}$.
  • POST(i) (warunek na końcu i-tego obrotu pętli): a i b są równe odpowiednio $f_{i+1}$ i $f_{i+2}$.

Pokażemy teraz, że warunki PRE(i) i POST(i) rzeczywiście zachodzą dla wszystkich i = 0, 1, $\ldots$, n-1.

  1. PRE(0) jest spełnione, gdyż na początku zerowej iteracji for, a i b mają wartości odpowiednio 0 i 1, czyli $f_0$ i $f_1$.
  2. Dla wszystich i, PRE(i) implikuje POST(i): z założenia na początku i-tego obrotu wartości a i b to odpowiednio $f_i$ i $f_{i+1}$. Wykonanie pętli powoduje zatem przypisanie: a = $f_{i+1}$ oraz b = $f_{i} + f_{i+1}$, czyli b = $f_{i+2}$.
  3. Dla wszystkich i, POST(i) jest równoważne z PRE(i+1).

Jak łatwo zauważyć, z warunków 1., 2. i 3. wynika indukcyjnie, że dla wszystkich i zachodzą PRE(i) i POST(i). W szczególności, zachodzi POST(n-1), zatem wartość a na zakończenie całej pętli wynosi $f_n$. Stąd fib(n) zwraca $f_n$.

Inny przykład poznanego algorytmu i warunków PRE i POST jego pętli: postfix_eval. Warunki można określić następująco:

  • PRE(i): Tokeny na stosie są liczbami, które połączone z nieprzetworzonymi tokenami stanowią poprawne wyrażenie ONP, którego wartość jest równa wartości oryginalnego. Nieprzetworzonych tokenów jest o i mniej, niż na początku algorytmu.
  • POST(i): Tokeny na stosie są liczbami, połączone z nieprzetworzonymi tokenami stanowią poprawne wyrażenie ONP, którego wartość jest równa wartości oryginalnego. Nieprzetworzonych tokenów jest o i+1 mniej, niż na początku algorytmu.

Selection sort - sortowanie przez wybieranie

Intuicyjne przedstawienie algorytmu selection sort: wyciągamy elementy z ciągu od najmniejszego do największego, ustawiając je po kolei. Rozważmy ciąg liczb. Najpierw szukamy wśród nich najmniejszej. Zamieniamy ją miejscami z pierwszą liczbą w ciągu. Następnie szukamy najmniejszej liczby wśród pozostałych. Zamieniamy ją z drugą liczbą w ciągu. Powtarzamy proces, aż do ostatniej liczby. W każdym kroku, na $i$-tą pozycję w ciągu kładziemy najmniejszą z liczb, które nam pozostały: zatem po zakończeniu procesu, ciąg jest posortowany.

Bardziej formalnie:

Kroki algorytmu selection_sort, w którym lst to lista, a n to jej długość:

  1. Dla i = 0, 1, $\ldots$, n - 1:
    1a. Znajdujemy minimalny element spośród lst[i], lst[i+1], $\ldots$, lst[n - 1].
    1b. Zamieniamy go miejscami z lst[i].

Sformułujemy warunki PRE i POST dla i-tej iteracji pętli z (jedynego) kroku 1. Ich dowody pominiemy, zauważymy jednak, że POST(n-1) jest równoważne z "cała lista jest posortowana", zatem dowód POST(n-1) jest jednocześnie dowodem poprawności algorytmu.

  • PRE(i): wszystkie elementy o indeksach $<$ i są uporządkowane i nie większe od elementów o indeksach $\geq$ i.
  • POST(i): wszystkie elementy o indeksach $\leq$ i są uporządkowane i nie większe od elementów o indeksach $>$ i.

Kod algorytmu w Pythonie:

def find_min_index(lst, start):
    i = start
    for j in range(i + 1, len(lst)):
        if lst[j] < lst[i]:
            i = j
    return i

def selection_sort(lst):
    for i in range(len(lst)):
        min_idx = find_min_index(lst, i)
        lst[i], lst[min_idx] = lst[min_idx], lst[i]

Poniżej ilustracja działania algorytmu: słupki reprezentują liczby na kolejnych indeksach listy. W i-tym kroku, liczba pod indeksem i (zielony słupek) jest zamieniana z największą liczbą pod indeksem nie mniejszym niż i (czerwony słupek):

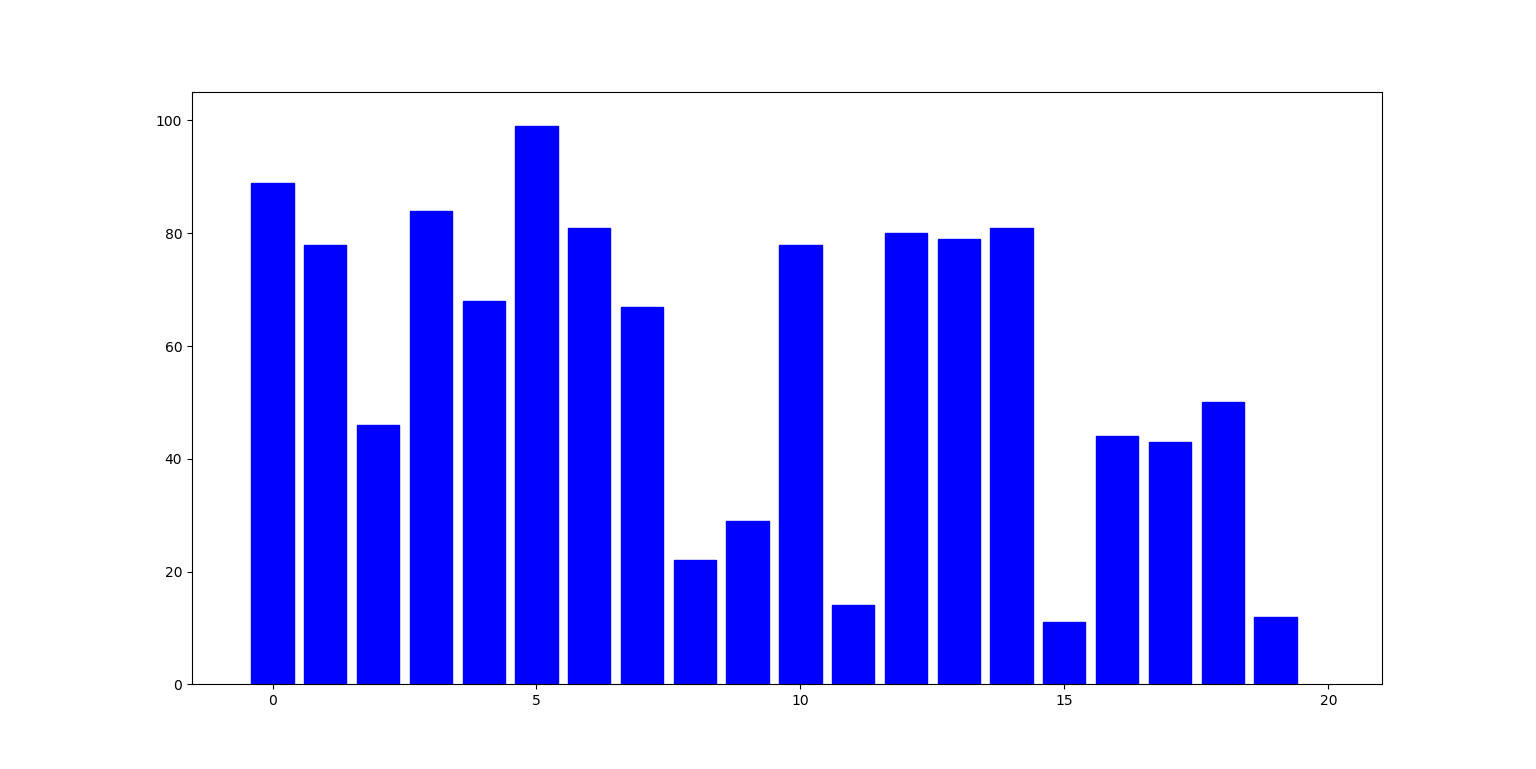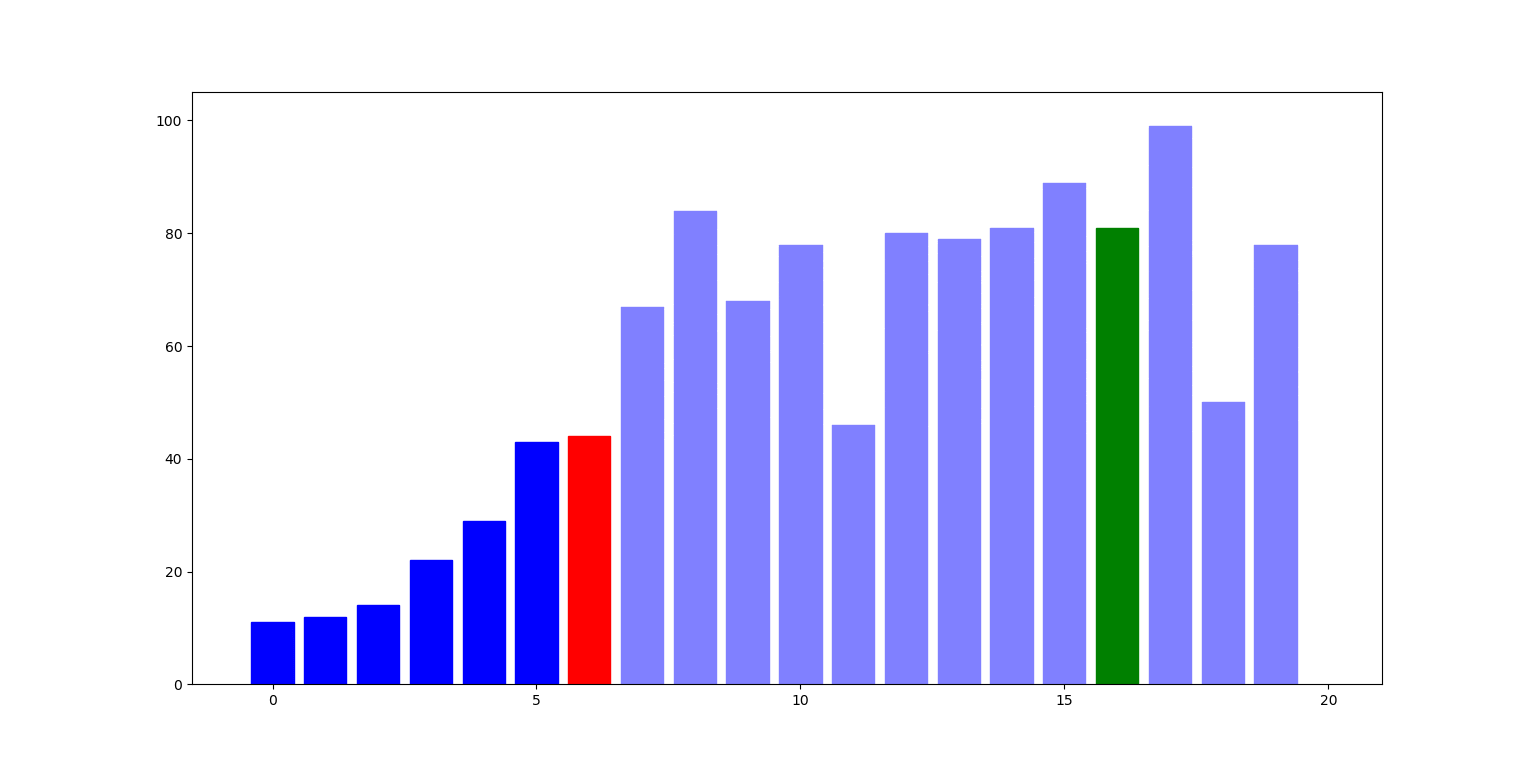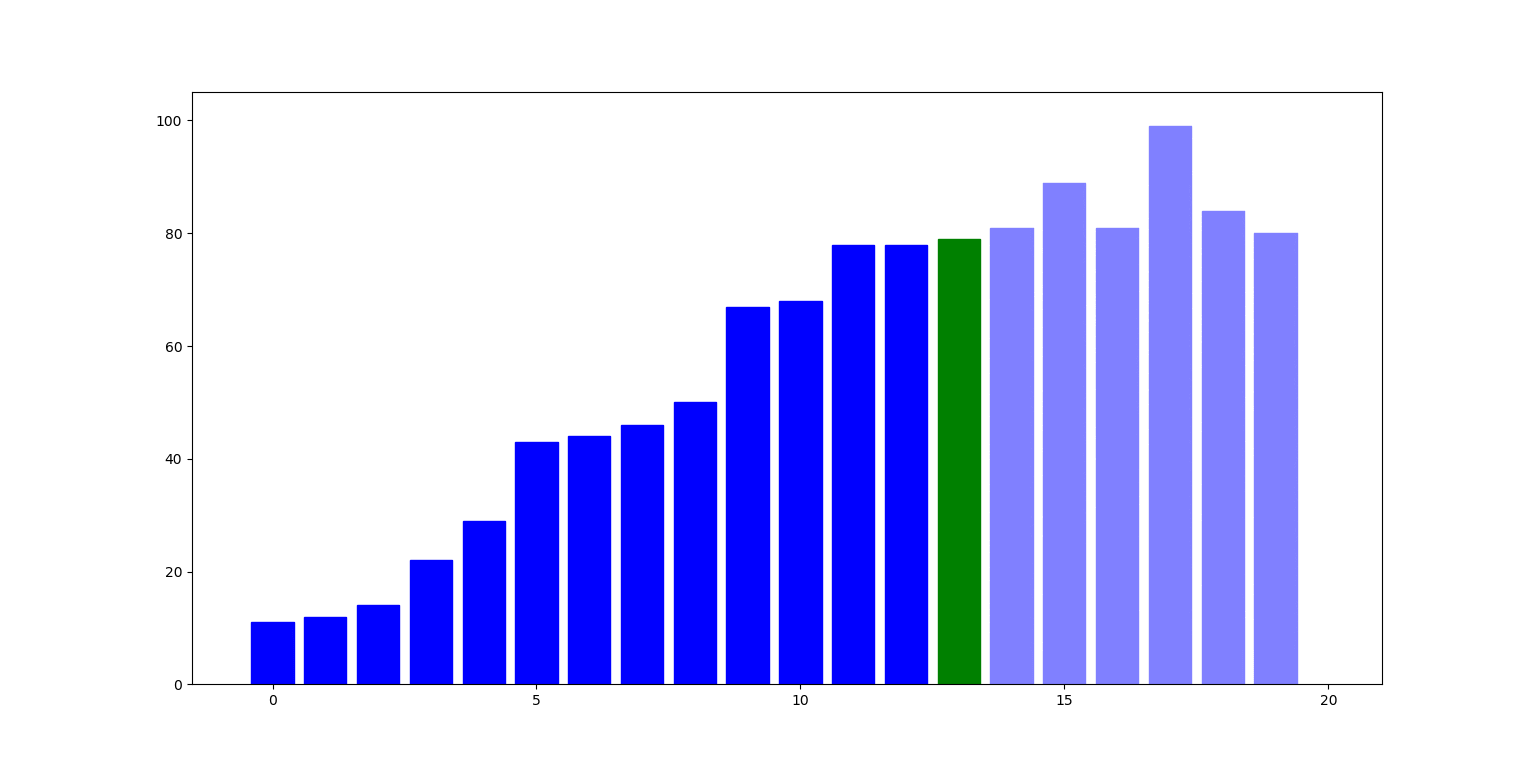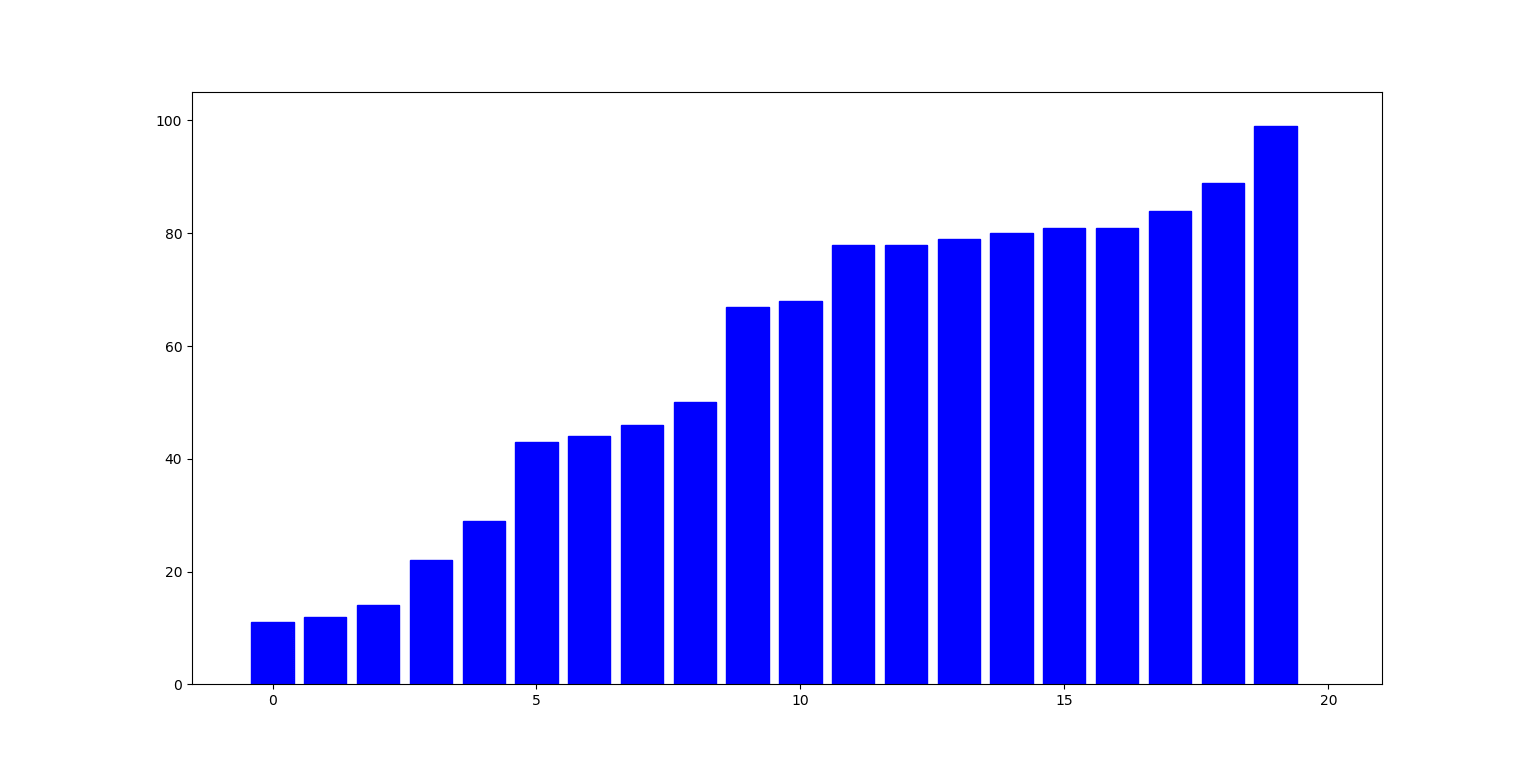
Zbadajmy teraz cechy tego algorytmu:

  • Złożoność czasowa: w $i$-tej iteracji pętli musimy wykonać $n - i - 1$ porównań, zatem algorytm zawsze działa w czasie $\Theta(n^2)$.
  • Złożoność pamięciowa: jedynie zmienne do kontroli pętli, zatem $\Theta(1)$.
  • Stabilność: NIE (zamiana elementu spod $i$-tego indeksu z innym może go przenieść za element, który jest mu równy).

Insertion sort - sortowanie przez wstawianie

Intuicyjne przedstawienie tego algorytmu: budujemy listę przez wstawianie kolejnych elementów na właściwą pozycję, jeśli trzeba przesuwając niektóre elementy. Znów rozważmy ciąg liczb. Jeśli druga z nich jest mniejsza od pierwszej, zamieniamy je miejscami. Przechodzimy do trzeciej. Zamieniamy ją miejscami z liczbami na lewo od niej tak długo, aż na lewo od niej nie będzie takiej, która jest od niej większa. Następnie powtarzamy to dla kolejnych liczb z ciągu. Po zakończeniu algorytmu, każda liczba zostaje wstawiona na swoje miejsce.

Znów w postaci algorytmicznej:

Kroki algorytmu insertion_sort (lst: lista, n: długość listy):

  1. Dla i = 0, 1, $\ldots$, n - 1:
    1a. Zapamiętujemy element x = lst[i].
    1b. Szukamy pierwszego indeksu j $\leq$ i takiego, że elementy o mniejszych indeksach są nie większe od lst[i].
    1c. Wstawiamy x pod indeks j poprzez zamienienie go miejscami z elementami o indeksach (kolejno) i-1, i-2, $\ldots$, j.

Podobnie formułujemy warunki PRE i POST dla i-tej iteracji zewnętrznej pętli (krok 1). Znów zauważamy, ze POST(n-1) oznacza posortowanie listy. W odróżnieniu od selection sort, PRE(i) nie zakłada nic o elementach na indeksach $\geq$ i.

  • PRE (i): wszystkie elementy o indeksach $<$ i są uporządkowane.
  • POST(i): wszystkie elementy o indeksach $\leq$ i są uporządkowane.

Przykładowa implementacja insertion sort. Tutaj przesuwamy element na jego pozycję przez ciągłą zamianę miejscami z elementem na lewo tak długo, aż element trafi na początek listy, lub element na lewo będzie od niego mniejszy lub równy.

def insertion_sort(lst):
    for i in range(1, len(lst)):
        j = i
        while j > 0 and lst[j - 1] > lst[j]:
            lst[j], lst[j - 1] = lst[j - 1], lst[j]
            j -= 1

Znów ilustracja działania. Czerwony słupek jest wstawiany na swoje miejsce, zamieniając się miejscami ze słupkami stojącymi na lewo od nim (zielone), aż trafi na swoje miejsce.

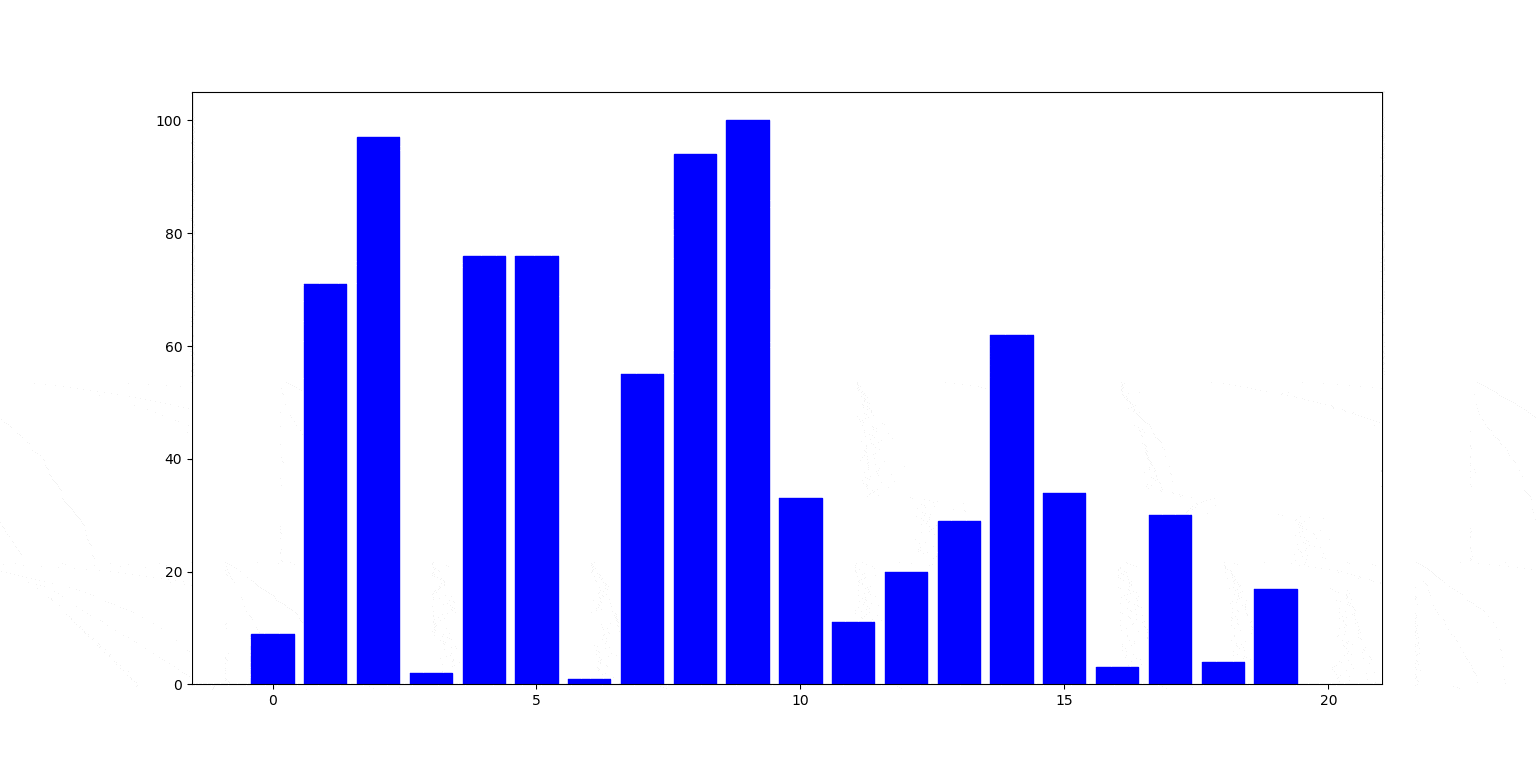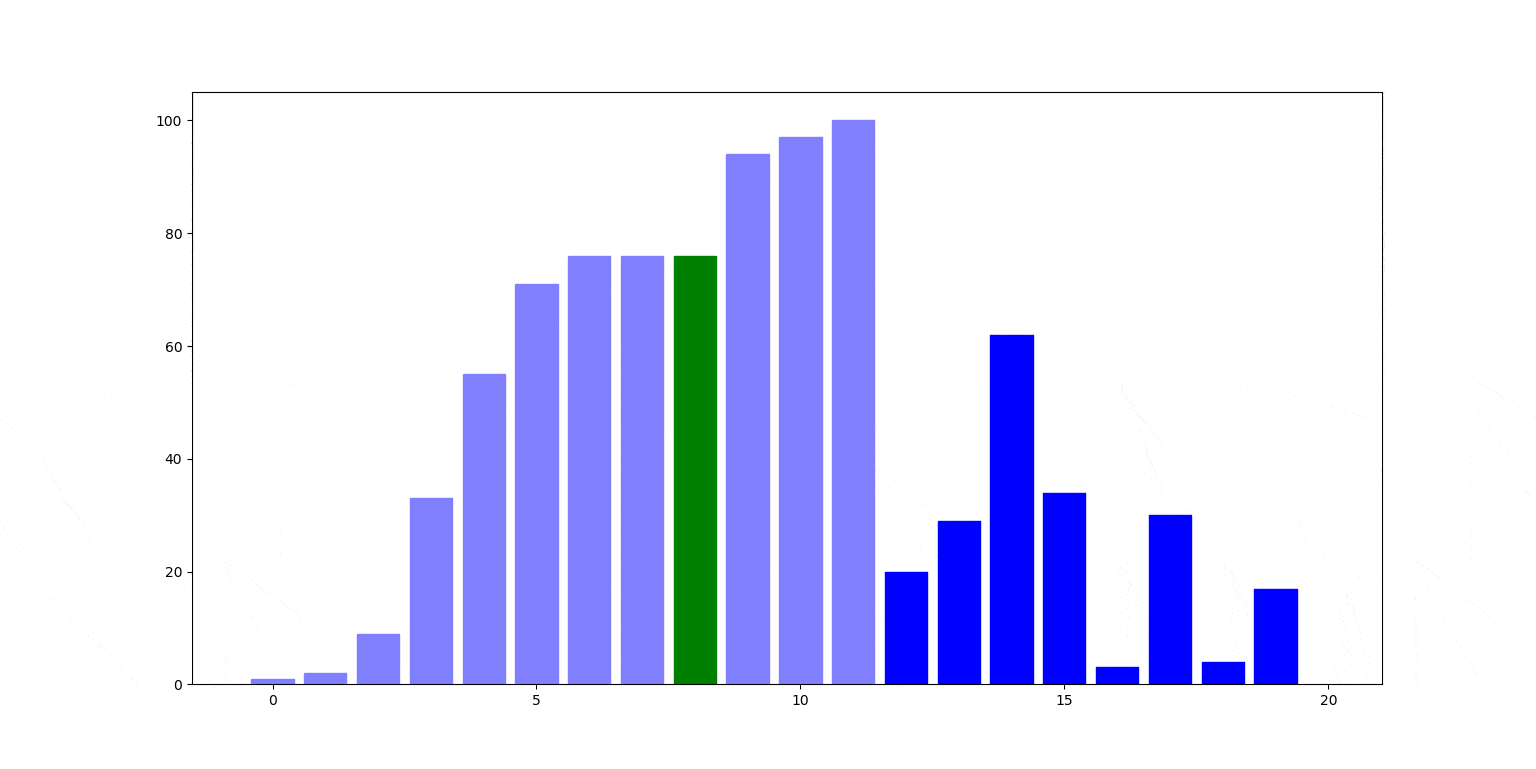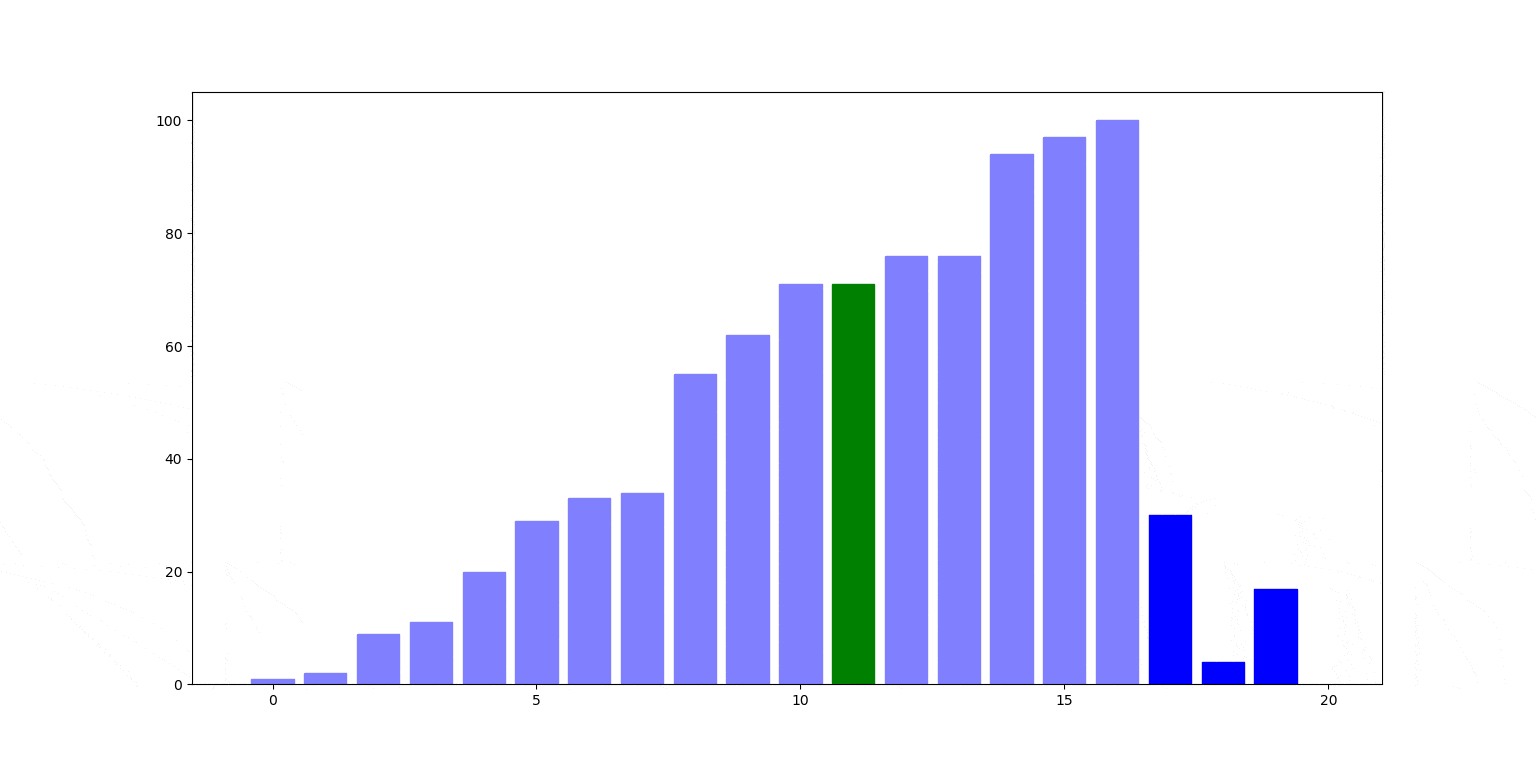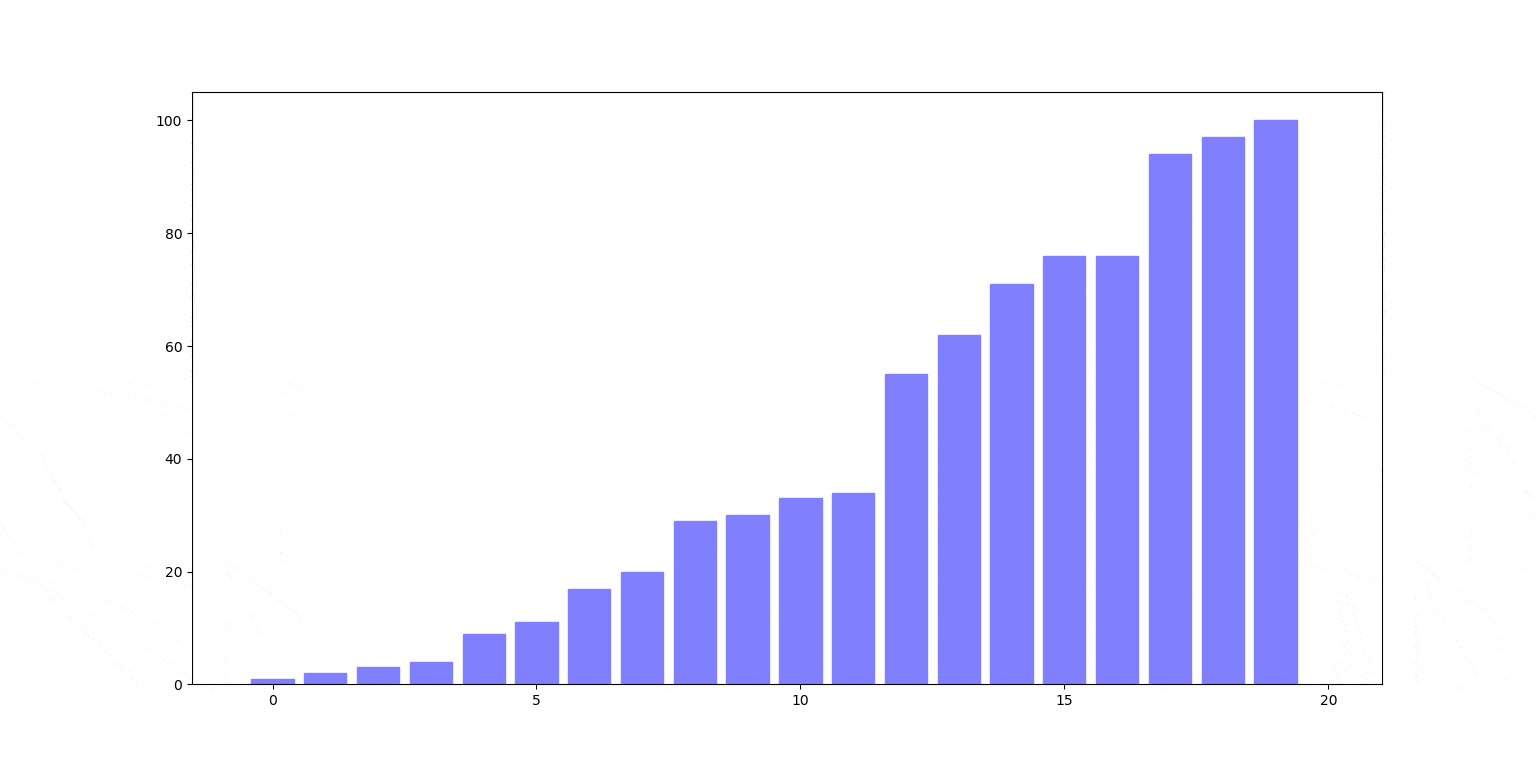
Cechy sortowania przez wstawianie:

  • Złożoność czasowa: W $i$-tej iteracji, przy przesunięciu elementu z indeksu $i$ na indeks $j \leq i$ wykona się między $1$ a $i$ porównań. Można rozróżnić przypadki:
  1. Jeśli lista jest posortowana, w każdej iteracji wykona się najmniejsza liczba porównań - tylko jedno. Żaden element nie zostanie ruszony z miejsca. Jest to przypadek optymistyczny. Optymistyczny czas działania algorytmu to zatem $\Theta(n)$.
  2. Jeśli lista jest posortowana malejąco, wtedy każdy element zostanie przemieszczony o największą możliwą ilość miejsc, i porównań wykona się maksymalna ilość. Jest to przypadek pesymistyczny, więc pesymistyczny czas działania insertion sort to $\Theta(n^2)$
  3. Przypadek średni. Nieformalnie: w statystycznej sytuacji wykona się połowa potencjalnych porównań, skąd czas średni to również $\Theta(n^2)$.
  • Złożoność pamięciowa: jedynie zmienne do kontroli pętli, zatem $\Theta(1)$.
  • Stabilność: TAK. Wstawienie elementu równego tym, które są już wstawione umieszcza go na prawo od niego - kolejność się zachowuje. Już wstawione elementy zachowują kolejność, gdy są przesuwane w prawo podczas wstawiania dalszych elementów.