G. Jagiella

Skrypt do wykładu Programowanie 2 (Python)

ostatnia modyfikacja: 31.05.2020

Wykład 9 - kopce binarne, kolejki priorytetowe, algorytm Dijkstry¶

Spis treści¶

Kopce binarne
Zastosowania kopców
- Heapsort (sortowanie przez kopcowanie)
- Kolejka priorytetowa
Algorytm Dijkstry

W tym rozdziale opiszemy strukturę danych znaną jako kopiec binarny i jego zastosowanie w implementacji kolejek priorytetowych. Następnie użyjemy kolejek priorytetowych w opisie i implementacji algorytmu Dijkstry, rozwiązującego problem znajdowania najkrótszej ścieżki w pewnej klasie grafów ważonych.

Kopce binarne ¶

Opis ¶

Niech $T$ będzie drzewem.

Definicja. Niech $n \in \mathbb{N}$. Zbiór węzłów odległych od korzenia o $n$ (licząc odległość w ilościach krawędzi prowadzących od korzenia do węzła) nazwiemy $n$-tym poziomem drzewa.

Korzeń jest na poziomie $0$, dowolne dziecko korzenia jest na poziomie $1$, etc.

Załóżmy teraz, że $T$ jest drzewem binarnym.

Fakt. Niech $n \in \mathbb{N}$. Wtedy:

Na $n$-tym poziomie $T$ znajduje się co najwyżej $2^n$ węzłów.

Na poziomach o numerze mniejszym od $n$ znajduje się co najwyżej $2^n - 1$ węzłów.

W drzewie wysokości $n$ znajduje się co najwyżej $2^n - 1$ węzłów.

Od teraz pozwalamy, aby drzewa były puste.

Drzewo $T$ nazywamy zupełnym (complete tree), gdy na każdym poziomie (wyłączając być może ostatni) $T$ ma wszystkie możliwe węzły, a węzły na ostatnim poziomie są możliwie najbardziej z lewej strony.

Uwaga. Drzewa zupełnego nie należy mylić z drzewem pełnym (full tree), innym rodzajem drzew binarnych.

Poniżej przykład zupełnego drzewa binarnego. Ostatnie dziecko na ostatnim poziomie jest koniecznie dzieckiem lewym.

Definicja. Binarne drzewo zupełne $(V, S)$, którego węzły przechowują parami porównywalne klucze nazywamy kopcem binarnym (binary heap), gdy $$\forall x, y \in V ~ x S y \implies \text{ klucz w }x \text{ jest nie większy od klucza w }y.$$

Przykład.

W kopcu, w każdej gałęzi, kolejne klucze są uporządkowane niemalejąco. Najmniejszy klucz znajduje się w korzeniu kopca.

Innymi nazwami (tak zdefiniowanego kopca) są m.in.: sterta, stóg, kopiec minimum (min-heap). Nierówność w definicji kopca można odwrócić, otrzymując analogiczny koncept, zwany kopcem maksimum (max-heap). W domyśle, kopce na wykładzie to kopce minimum.

Kopiec traktujemy jako strukturę danych, przechowującą klucze w węzłach. Rozważmy następujące operacje, jakie chcemy móc wykonać na kopcu:

insert_key(key): włóż nowy węzeł o zadanym kluczu.
extract_min(): usuń węzeł z minimalnym kluczem i zwróć wartość klucza.
(opcjonalnie) decrease_key(key, new_value): zmniejsz wartość podanego klucza.
(opcjonalnie) increase_key(key, new_value): zwiększ wartość podanego klucza.

Wszystkie powyższe operacje muszą zachować własność kopca: po dodaniu/usunięciu węzła lub zmianie wartości klucza trzeba zapewnić, że nowo powstałe drzewo binarne spełnia definicję kopca.

W operacjach decrease_key i increase_key zakładamy, że klucze w kopcu są unikalne.

Kluczowym elementem implementacji powyższych operacji jest tzw. kopcowanie, czyli naprawianie własności kopca.

Kopcowanie i realizacja operacji ¶

Rozważmy kopiec, w którym klucz w pewnym węźle $t$ zastępujemy innym tak, że własność kopca została naruszona. Są dwie możliwości:

Nowy klucz w $t$ jest mniejszy, niż klucz w rodzicu $t$, lub
Klucz w lewym lub prawym dziecku $t$ jest mniejszy, niż nowy klucz w $t$.

Zwracamy uwagę, że skoro przed operacją podmiany klucza drzewo było kopcem, 1. i 2. nie mogą zajść jednocześnie.

W sytuacjach 1. i 2. własność kopca da się naprawić permutując klucze przyporządkowane do węzłów tak, aby otrzymać kopiec. Służą do tego tak zwane algorytmy kopcowania odpowiednio "w górę" lub "w dół" (dla przypadków 1. i 2. odpowiednio). Poniżej podajemy opis algorytmów, potem przejdziemy do przykładów:

Kopcowanie w górę: kroki heapify_up, gdzie t - węzeł.

Jeśli t jest korzeniem kopca, koniec.

Jeśli klucz w t jest mniejszy, niż klucz w rodzicu t:
2a. Zamień miejscami klucze w t i rodzicu t.
2b. Wróć do kroku 1. zastępując t przez rodzica t.

Kopcowanie w dół: kroki heapify_down, gdzie t - węzeł:

Jeśli klucz w t jest nie większy, niż klucz w dowolnym dziecku t, koniec.

W przeciwnym wypadku, niech s będzie dzieckiem t o minimalnym kluczu.
2a. Zamień miejscami klucze w s i t.
2b. Wróć do kroku 1. zastępujac t przez s.

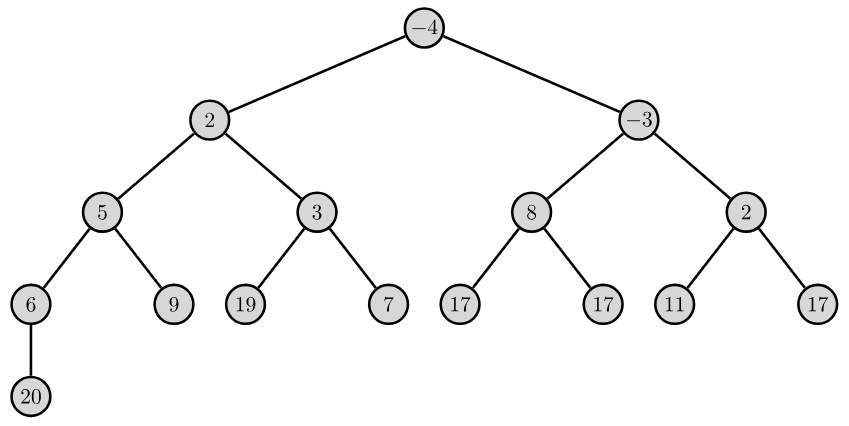
W przykładach poniżej będą pojawiać się zupełne drzewa binarne, w których jeden wierzchołków zaprzecza własności kopca: ma klucz wiekszy niż co najmniej jedno dziecko, lub mniejszy niż rodzic. Będziemy kolorować na czerwono krawędź łączącą takie złe pary wierzchołków.

Przykład (kopcowanie w górę). Poniższe zupełne drzewo binarne byłoby kopcem, gdyby w liściu z kluczem $4$ znajdował się większy klucz (np. $100$). Przeprowadzamy kopcowanie w górę, zaczynając od liścia z kluczem $4$:

1. Stan początkowy: 2. Po zamianie 4 z 11: 3. Po zamianie 4 z 7 jest kopiec:

Przykład (kopcowanie w dół). Rozważmy tym razem kopiec, w którym korzeń przechowuje klucz większy, niż jego dziecko (tutaj: i lewe, i prawe). Kopcujemy w dół począwszy od korzenia:

1. Stan początkowy: 2. Po zamianie 17 z 12: 3. Po zamianie 17 z 15 jest kopiec:

Pominiemy formalne uzasadnienie poprawności obu algorytmów, tzn. że dla zupełnego drzewa binarnego w którym co najwyżej jeden wierzchołek przeczy własności kopca odpowiedni algorytm kopcowania przekształca drzewo do kopca o tych samych kluczach.

Fakt. Złożoność obu algorytmów to $O(\log n)$, gdzie $n$ to ilość węzłów w kopcu.
Dowód. Każdy krok algorytmu kopcowania w górę polega na porównaniu kluczy w pewnych węzłach i dokonaniu zamiany kluczy. Z każdą zamianą, wierzchołek przeczący własności kopca przesuwa się o jeden poziom w górę, lub algorytm kończy działanie. Kroków będzie zatem nie więcej niż wysokość drzewa. Podobnie dla kopcowania w dół.

Zauważmy, że w kopcowaniu w dół nie mamy pełnej dowolności w zamianie klucza węzła z kluczem jego dziecka: klucz dziecka, z którym się zamieniamy zostaje kluczem w rodzicu drugiego dziecka, nie może być więc od niego większy. Przykładowo, gdyby w pierwszym kroku drugiego przykładu zamienić miejscami $17$ i $14$, wtedy korzeń zawiera $14$, a jego prawe dziecko $12$.

Kopcowania pomagają przywrócić własność kopca m.in. gdy:

Zmniejszamy wartość klucza w węźle - wystarczy wtedy dokonać kopcowania w górę począwszy od tego węzła.
Zwiększamy wartość klucza w węźle - wystarczy wtedy dokonać kopcowania w dół począwszy od tego węzła.

Ta obserwacja pozwala na prosty opis operacji insert_key, extract_min i pozostałych:

Kroki insert_key dla klucza key:

Wstaw nowy liść t o kluczu key, tak, aby drzewo wciąż było zupełne.

Wykonaj heapify_up na t.

Kroki extract_min:

Zapisz klucz z korzenia kopca w x

Przepisz klucz z ostatniego liścia kopca do korzenia i usuń ten liść.

Wykonaj heapify_down na korzeniu kopca.

Zwróć x.

Kroki increase_key, key - klucz, new_value - nowa wartość klucza:

Niech t: węzeł z kluczem key. Zastąp klucz w t przez new_value.

Wykonaj heapify_down na t.

Kroki decrease_key, key - klucz, new_value - nowa wartość klucza:

Niech t: węzeł z kluczem key. Zastąp klucz w t przez new_value.

Wykonaj heapify_up na t.

Stwierdzenie. Zdefiniowane wyżej działanie insert_key i extract_min i pozostałych operacji zachowuje własność kopca.
Dowód. insert_key: dołączenie do drzewa nowego liścia z podanym kluczem jest równoważne z parą operacji: dostawienie nowego liścia z kluczem $\infty$ (gdzie $\infty$ to sztuczny klucz większy lub równy od każdego innego; ta operacja zachowuje własność kopca) a następnie zastąpieniu $\infty$ przez właściwy, podany klucz (czyli zmniejszenie klucza, po którym kopiec daje się naprawić przez heapify_up rozpoczynający od tego nowego liścia). extract_min: Usunięcie liścia zachowuje własność kopca, a po podmianie klucza w korzeniu na większy kopiec naprawia się przez heapify_down zaczynający w korzeniu. Pozostałe operacje: analogicznie.

Poniżej animacja pokazująca wstawianie nowego elementu do kopca (insert_key dla klucza $4$). Na różowo zaznaczone są pary rodzic-dziecko, których klucze porównujemy i zamieniamy miejscami:

Analogiczna animacja pokazująca działanie extract_min na innym kopcu:

Przy założeniu, że operacja dołożenia nowego liścia oraz znalezienia węzła o podanym kluczu to operacje o złożoności co najwyżej logarytmicznej, mamy:

Fakt. Złożoność wszystkich operacji kopcowych to $O(\log n)$, gdzie $n$ to ilość węzłów w kopcu.
Dowód. Każda operacja kopcowa składa się ze stałej ilości operacji oraz jednego wywołania algorytmu kopcowania (w górę lub w dół).

Kopce jako listy ¶

Konceptualnie, o kopcach myślimy jako o zupełnych drzewach binarnych. Kopce można jednak reprezentować w prosty sposób przy użyciu list. W ustalonym zupełnym drzewie binarnym o $n$ węzłach, możemy te węzły jednoznacznie ponumerować liczbami $0, 1, \ldots, n - 1$ zaczynając od węzłów na poziomach o niższym numerze i tych po lewej stronie, np.:

Taką przypisaną liczbę nazwiemy indeksem węzła.

Łatwo wyprowadzić konkretne zależności między indeksami a położeniem węzłów w drzewie. Rozważmy węzeł $t$ o indeksie $i$.

Jeśli węzeł jest $x$-tym węzłem na poziomie $y$, to $i = 2^y + x - 1$ (węzły na ustalonym poziomie numerujemy od $0$).
Rodzic $t$ (jeśli istnieje) ma indeks $\lfloor(i-1)/2\rfloor$.
Lewe dziecko $t$ (jeśli istnieje) ma indeks $2 \cdot i + 1$.
Prawe dziecko $t$ (jeśli istnieje) ma indeks $2 \cdot i + 2$.

Zamiast reprezentować kopiec jako węzły, pamiętające lewe i prawe poddrzewa oraz klucze, możemy więc reprezentować kopiec jako listę długości takiej, jak ilość węzłów w nim. Elementami listy są klucze, pamiętane przez kopiec: klucz pamiętany przez węzłł o indeksie $i$ znajduje się na liście pod tym właśnie indeksem. Indeksami posługujemy się w zastępstwie wierzchołków. Dzięki podanym wyżej zależnościom arytmetycznym, dla danego indeksu (węzła) łatwo uzyskać dostęp do (indeksu) jego wybranego dziecka lub rodzica. Sprawdzenie, czy dziecko lub rodzic istnieją jest tożsame ze sprawdzeniem, czy jego indeks jest legalnym indeksem na liście.

Przykładowo, nastepujące drzewo (kopiec) z przykładu wyżej:

można reprezentować jako listę [12, 14, 15, 20, 22, 20, 17].

Wszystkie algorytmy kopcowe dają się więc przetłumaczyć jako algorytmy operujące na indeksach i zawartości listy reprezentującej kopiec. Na szczególną uwagę zasługują dwie operacje: dodawanie nowego liścia oraz usuwanie ostatniego liścia. Te operacje tłumaczą się na dołożenie (odpowiednio usunięcie) ostatniego elementu na liście. Te operacje to po prostu append i pop, a one wykonują się w czasie stałym.

Implementacja ¶

W katalogu structures znajdują się dwa warianty implementacji kopców.

W min_heap1.py znajduje się uproszczona klasa MinHeap.
W min_heap.py znajduje się właściwa klasa MinHeap.

Obie wersje implementują podstawowe operacja kopcowe (insert_key i extract_min). Wersja właściwa implementuje dodatkowo decrease_key oraz pewne metody dla wygody. Obie implementacje używają wewnętrznie listy do reprezentacji kopca i ukrywają ten fakt przed użytkownikiem (w szczególności nie używają indeksów węzłów do komunikacji z nim).

Interfejs wersji uproszczonej jest nastepujący:

__init__(self): - tworzy pusty kopiec.
is_empty(self) - sprawdza, czy kopiec jest pusty.
insert_key(self, key) - wkłada do kopca klucz key.
peek(self) - zwraca (nie usuwa) najmniejszy klucz w kopcu.
extract_min(self) - usuwa i zwraca najmniejszy klucz z kopca.
size(self) - zwraca rozmiar kopca.

Wewnętrznie, ta wersja MinHeap używa jeszcze następujących metod:

heapify_up(self, i) - kopcuje w górę, począwszy od węzła o indeksie i.
heapify_down(self, i) - kopcuje w dół, począwszy od węzła o indeksie i.
parent(i) - zwraca indeks węzła o indeksie i.
left_child(i) - zwraca indeks lewego dziecka węzła o indeksie i.
right_child(i) - zwraca indeks prawego dziecka węzła o indeksie i.

Ostatnie trzy metody (parent, left_child, right_child) nie mają parametru self i ich deklaracja jest poprzedzona niewyjaśnionym napisem @staticmethod. Taki sposób deklaracji metody czyni z niej tzw. metodę statyczną. Jest to zwykła funkcja, która nie wymaga instancji MinHeap do działania, ale jest zdefiniowana wewnątrz klasy MinHeap. Można jej używać w następujący sposób:

parent = MinHeap.parent(i) # parent = rodzic i

Metody statyczne tworzymy na przykład wtedy, gdy potrzebujemy funkcji ściśle związanej z definicją (implementacją) danej klasy, ale nie wykorzystującej jej instancji. W tej sytuacji, metody parent związane są z tłumaczeniem indeksów reprezentujących wierzchołki w implementacji MinHeap. Same indeksy jednak to zwykłe liczby.

Wewnętrznie, kopiec przechowywany jest jako lista (atrybut heap). Operacje kopcowe i kopcowanie zaimplementowane są bezpośrednio przepisując algorytmy. Dołożenie i usuwanie ostatniego liścia tłumaczą się (zgodnie z opisem reprezentacji kopca jako listy) na append i pop.

W wersji właściwej, klasa MinHeap implementuje dodatkowo:

__init__(self, values=()) - konstruktor, który tworzy pusty stos i odkłada na nim klucze z opcjonalnego iterowalnego parametru values.
decrease_key(self, key, new_val) - zmniejsza klucz key na wartość new_val.
__iter__(self) - zwraca iterator, zwracający ściągane z kopca klucze aż do ich wyczerpania.

Wewnętrznie klasa używa też:

decrease_key_at_index(self, i, new_val): zmniejsza klucz pod indeksem i na wartość new_val.

Ta implementacja wymaga, aby klucze w kopcu były unikalne i hashowalne.

Implementacja rozszerza poprzednią w jeden istotny sposób. Do efektywnego działania decrease_key konieczne jest, aby znajdywanie węzła (czyli indeksu) podanego klucza dokonywało się w czasie co najwyżej logarytmicznym. Aby to umożliwić, klasa trzyma słownik (atrybut keys) stowarzyszający klucze z indeksami, pod którymi występują. Dla wszystkich kluczy i indeksów prawdziwe jest: "self.keys[k] == i wtedy i tylko wtedy, gdy self.heap[i] == k". Słownik ten uaktualniamy za każdym razem, gdy klucze są wstawiane lub usuwane z listy heap lub gdy ich wartości są zmieniane. W szczególności, wymagało to zmian między innymji w metodach kopcowania.

Zastosowania kopców ¶

Heapsort (sortowanie przez kopcowanie)¶

Prostym zastosowaniem kopca jest algorytm Heapsort, czyli sortowanie przez kopcowanie. Dla podanej listy lst parami porównywalnych elementów, tworzymy kopiec (na przykład odkładając elementy z listy do nowoutworzonego, pustego kopca), następnie wyciągamy z niego elementy aż do wyczerpania. Elementy są wyciągane w kolejności od najmniejszego, do największego.

Przykładowa implementacja:

from structures.min_heap import MinHeap # structures - katalog

def heap_sort(lst):
    return list(MinHeap(lst))  # to cały algorytm - korzysta z __iter__ dla MinHeap

lst = [763, 254, 675657, 67, 35, 56756, 674, 2, 7689, 34]
lst_sorted = heap_sort(lst)
print(lst_sorted)
assert lst_sorted == sorted(lst)

lst = ["dog", "cat", "bat", "hog", "zebra", "hamster", "emu"]
lst_sorted = heap_sort(lst)
print(lst_sorted)
assert lst_sorted == sorted(lst)

[2, 34, 35, 67, 254, 674, 763, 7689, 56756, 675657]
['bat', 'cat', 'dog', 'emu', 'hamster', 'hog', 'zebra']

Uwagi:

Złożoność algorytmu: nietrudno pokazać $O(n \log n)$: dla każdego z $n$ elementów wykonamy po jednym włożeniu i wyjęciu, a obie te opercje nie zadziałają w czasie gorszym niż $O(\log n)$ (bo kopiec nigdy nie będzie większy, niż $n$ elementów). Dokładniejsza analiza pokazuje, że czasy działania to $\Theta( n \log n)$ w przypadku średnim i pesymistycznym, oraz $\Theta(n)$ w optymistycznym.
Złożoność pamięciowa: $\Theta(n)$. Można też zmodyfikować algorytm tak, aby działał w miejscu (używał podanej listy jako listy reprezentującej stos).
Nie jest stabilny (a w pewnym sensie jest bardzo niestabilny).
Wydajny w porównaniu z innymi algorytmami.
Używany do usprawnienia algorytmów typu "dziel i rządź", np. Introsort - hybryda Quicksorta i Heapsorta. W Introsort najpierw wykonywany jest Quicksort, ale gdy głębokość rekurencji przekroczy pewną wartość (zależną logarytmicznie od długości listy), algorytm przełącza się na Heapsort, aby zagwarantować czas $O(n \log n)$.

Kolejka priorytetowa ¶

Kolejka priorytetowa to struktura danych, do której możemy wkładać obiekty oraz je z niej wyjmować. Obiekty wkładamy do kolejki wraz z ich priorytetami (dowolnymi, parami porównywalnymi obiektami). Obiekty wyciągamy z kolejki zgodnie z ich priorytetami: najpierw te o niższym priorytecie (może to być niezgodne z intuicją, ale jest przydatne w dalszych zastosowaniach). Priorytety obiektów w kolejce mogą ulegać zmianie po włożeniu tych obiektów.

Przykład "z życia" kolejki priorytetowej to np. samoloty oczekujące na lądowanie na lotnisku: najpierw obsługiwane są te, które mają mniej paliwa.

Zwróćmy uwagę, że pewne dobrze nam znane struktury danych można interpretować jako szczególne rodzaje kolejek priorytetowych:

Kolejka (zwykła): elementy wyciągamy w kolejności wkładania (priorytem jest więc czas włożenia).
Stos: elementy wyciągamy w kolejności odwrotnej (priorytetem jest minus czas włożenia).

Kolejkę priorytetową możemy zaimplementować z użyciem kopca. Opiszemy sposób takiej implementacji przy założeniu, że dane kładzione do kolejki są unikalne i parami porównywalne (jest to założenie, które łatwo obejść). W typowej sytuacji dane to napisy, liczby etc.

Kolejkę priorytetową reprezentujemy jako kopiec, w którym kluczami są pary (priorytet, dane). Włożenie do kolejki obiektu dane z priorytetem priorytet utożsamiamy z włożeniem do kopca takiej pary. Czynimy przy tym obserwacje:

Pary (priorytet, dane) są uporządkowane leksykograficznie i każde dwie takie pary są porównywalne (gwarantuje to założenie o porównywalności danych). Mogą zatem być kluczami w kopcu, który obsługuje operacje decrease_key i increase_key.
Jeśli dla par (priorytet1, dane1) i (priorytet2, dane2) zachodzi priorytet1 $<$ priorytet2, to (zgodnie z definicją porządku leksykograficznego) mamy również (priorytet1, dane1) $<$ (priorytet2, dane2).
W konsekwencji powyższego, w korzeniu kopca zawsze znajduje się para (priorytet, dane), dla której priorytet jest najmniejszy możliwy.

Na mocy trzeciej obserwacji zauważamy, że operacja wyciągania elementu z kolejki priorytetowej tłumaczy się na wykonanie extract_min na kopcu: ta ekstrakcja zwraca nam dane o najniższym możliwym priorytecie (wraz z tym priorytetem).

Jeżeli znamy priorytet priorytet stowarzyszony z danymi dane w kolejce, możemy zmienić ten priorytet na nowy priorytet nowy_priorytet, zmieniając w kopcu klucz (priorytet, dane) na (nowy_priorytet, dane), używając decrease_key lub increase_key w zależności od tego, czy nowy_priorytet jest mniejszy czy większy od priorytet.

Algorytm Dijkstry ¶

Opis ¶

Algorytm Dijkstry to algorytm rozwiązujący zagadnienie znajdowania najkrótszej ścieżki sformułowane dla grafów skierowanych z wagami. Dla takich grafów inaczej definiujemy długość ścieżki, a w konsekwencji pojęcie odległość między wierzchołkami.

Definicja. Niech $G = (V, E, f)$ będzie grafem ważonym, a $S = (e_1, e_2, \ldots, e_n)$ ścieżką (skierowaną lub nie). Definiujemy długość $S$ jako sumę wag jej krawędzi: $L(S) = \sum_{i=1}^n f(e_i)$.

Definicja. Grafem dodatnio ważonym nazywamy graf ważony, w którym wagi wszystkich krawędzi są dodatnie.

Dla grafów dodatnio ważonych możemy definiować pojęcie odległości analogicznie, jak dla grafów bez wag, otrzymując pojęcie odległości (lub "odległości niesymetrycznej") między wierzchołkami.

Zajmiemy się teraz problemem wyszukiwania najkrótszej ścieżki (skierowanej) w grafie dodatnio ważonym. Założenie o dodatnich wagach jest istotne, ponieważ bez niego może zajść sytuacja, że dla pewnych wierzchołków $u, v$ istnieje ścieżka z $u$ do $v$, lecz nie istnieje ścieżka najkrótsza. Najprostszym przykładem tej sytuacji jest wierzchołek $u$ i krawędź z $u$ do $u$ o wadze ujemnej.

Niech dany będzie dodatnio ważony $G = (V, E, f)$ oraz wierzchołek źródłowy $u$. Opiszemy algorytm, który każdemu wierzchołkowi z silnej komponenty spójności $t_0$ (czyli każdemu wierzchołkowi, do którego prowadzi ścieżka z $u$) przypisze jego odległość od $u$ oraz wyznaczy ścieżkę zaświadczającą o tej odległości. Algorytm będzie używał pewnych konceptów zbliżonych do tych z poznanego już algorytmu przeszukiwania wszerz:

Każdy wierzchołek w grafie będzie miał dwa możliwe kolory: biały i czarny, reprezentujące odpowiednio wierzchołek nieodwiedzony i odwiedzony.
Każdemu wierzchołkowi zostanie przypisana jego tymczasowa odległość od $u$. Te tymczasowe odległości będą zmniejszać się w trakcie działania algorytmu, ale nigdy nie będą mniejsze niż rzeczywiste odległości.
Algorytm w kolejnych krokach będzie odwiedzał wierzchołki. Zawsze najpierw będzie odwiedzany wierzchołek o najmniejszej odległości tymczasowej.
Odwiedzanie wierzchołka będzie mogło powodować zmniejszenie odległości tymczasowych przypisanych niektórym jego sąsiadom (tak zwana relaksacja odległości).
Po wykonaniu algorytmu, odległości tymczasowe pokryją się z rzeczywistymi.

Kroki algorytmu dijkstra dla grafu G i wierzchołka początkowego u:

Oznacz wszystkie wierzchołki G jako nieodwiedzone.

Przypisz każdemu wierzchołkowi G odległość tymczasową $\infty$ i 0 dla u.

Dopóki w G są nieodwiedzone wierzchołki:
3a. Wybierz nieodwiedzony wierzchołek t o najmniejszej tymczasowej odległości.
3b. Oznacz t jako odwiedzony.
3c. Dla każdego nieodwiedzonego sąsiada s wierzchołka t: niech l $=$ (odległość tymczasowa do t) $+$ (waga krawędzi z t do s). Jeśli l jest mniejsze niż odległość tymczasowa do s, zmień tę odległość na l.

Wytłumaczmy teraz znaczenie kroku 3c. Niech $t$ będzie odwiedzanym wierzchołkiem, a $s$ jego (nieodwiedzonym) sąsiadem. Oznaczmy przez $d_t$ odległość tymczasową przypisaną $t$. O ile założymy, że $d_t$ jest nie mniejsza, niż prawdziwa odległość ze źródła $u$ do $t$, to wiemy, że istnieje ścieżka $S$ z $u$ do $t$ długości co najwyżej $d_t$. Jeśli więc krawędź z $t$ do $s$ ma wagę $m$, to istnieje też scieżka z $u$ do $s$ (złożona z $S$ i krawędzi łączącej $t$ z $s$) długości co najwyżej $d_t + m$. W takim razie, jeśli odległość tymczasowa przypisana $s$ jest większa niż $d_t + m$, można ją zmniejszyć (zrelaksować) do $d_t + m$, uzyskując lepsze górne ograniczenie prawdziwej odległości.

Zwróćmy uwagę, że odległości tymczasowe odwiedzonych wierzchołków nie mogą się już zmienić. Niedługo pokażemy, że z chwilą odwiedzenia wierzchołka $t$, przypisana mu odległość tymczasowa pokrywa się z rzeczywistą.

Zilustrujmy przykładowe działanie algorytmu Dijkstry na grafie z rozdziału o przeszukiwaniu wszerz, uzupełnionego o pewne wagi krawędzi. Kolorem pomarańczowym zaznaczamy wierzchołek, który zostanie odwiedzony (po czym od razu przekolorowany on zostaje na czarno), a następnie jego kolejne nieodwiedzone sąsiady, dla których badamy, czy należy zrelaksować ich odległości tymczasowe.

Ustalmy graf dodatnio ważony $G = (V, E, f)$ i wierzchołek źródłowy $u$.

Stwierdzenie. Z chwilą odwiedzenia wierzchołka, jego odległośc tymczasowa jest równa faktycznej odległości od $u$.
Dowód. Oznaczmy przez $B$ zbiór wierzchołków odwiedzonych w dowolnym kroku algorytmu. Pokażemy indukcyjnie ze względu na $|B|$, że odległości tymczasowe wierzchołków z $B$ zgadzają się z prawdziwą.

Gdy $|B| = 1$, wtedy $B = \{u\}$. Odległość tymczasowa $u$ wynosi $0$.

Rozważmy krok algorytmu, w którym odwiedzamy wierzchołek $v \neq u$ i że dla zbioru $B$ wierzchołków odwiedzonych przed $v$ zachodzi teza indukcyjna. Niech $d_v$ oznacza odległość tymczasową przypisaną $v$. Załóżmy nie wprost, że istnieje ścieżka $S = (e_1, e_2, \ldots, e_n)$ z $u$ do $v$ krótsza niż $d_v$. Skoro ścieżka łączy wierzchołek $u \in B$ z wierzchołkiem $v \notin B$, istnieje w niej krawędź $e_i = (x, y)$ taka, że $x \in B$ i $y \notin B$. Oznaczmy przez $S_x$ początkowy kawałek ścieżki $S$, prowadzący z $u$ do $x$ (czyli $S_x= (e_1, \ldots, e_{i-1})$). Oznaczmy długości $S$ i $S_x$ odpowiednio przez $L(S)$ i $L(S_x)$, a odległości tymczasowe $x$ oraz $y$ odpowiednio $d_x$ i $d_y$. Z założenia nie wprost, $$L(S) < d_v.$$ Ponieważ $x \in B$, z założenia indukcyjnego $d_x$ to długość najkrótszej ścieżki z $u$ do $x$, zatem $d_x \leq L(S_x)$ i stąd też: $$d_x + f((x, y)) \leq L(S_x) + f((x, y)),$$ gdzie $f((x, y))$ to waga krawędzi $(x,y)$. W kroku, w którym $x$ został odwiedzony, odległość tymczasowa $y$ została zrelaksowana do $d_x + f((x, y))$, chyba że już była mniejsza lub równa tej wartości. Stąd, $$d_y \leq d_x + f((x, y)).$$ Ponieważ wierzchołek $v$ został wybrany do odwiedzenia przed wierzchołkiem $y$, $$d_v \leq d_y.$$ Łącząc wszystkie nierówności, $$d_v \leq d_y \leq d_x + f((x, y)) \leq L(S_x) + f((x, y)) \leq L(S) < d_v,$$ co daje sprzeczność z założeniem nie wprost. To pokazuje, że teza indukcyjna zachodzi też dla zbioru $B' = B \cup \{v\}$ wierzchołków odwiedzonych uzupełnionych o nowoodwiedzony $v$.

Opisany algorytm znajduje więc odległości wierzchołków od źródła $u$. Pokażemy jego drobną modyfikację, która pozwoli na konstrukcję najkrótszych ścieżek, zaświadczających o tym odległościach.

Rozważmy krok algorytmu, w którym odległość tymczasowa wierzchołka $s \neq u$ zostaje zrelaksowana po raz ostatni. Staje się to w czasie odwiedzania wierzchołka $x$, którego odległość tymczasowa $d_x$ równa się prawdziwej, a odległość tymczasowa (a więc i prawdziwa) $y$ jest relaksowana do $d_x + f((x, y))$. Skoro więc istnieje ścieżka z $u$ do $x$ długości $d_x$, to ścieżka ta powiekszona o krawędź $(x, y)$ ma długość $d_x + f((x, y))$, a więc jest (pewną) najkrótszą ścieżką z $u$ do $s$. Dokonując relaksacji odległości tymczasowej $s$ możemy zapamiętywać wierzchołek, który jest odwiedzany w czasie tej relaksacji, modyfikując odpowiedni krok algorytmu:

3c. (zmieniony) Dla każdego nieodwiedzonego sąsiada s wierzchołka t: niech l $=$ (odległość tymczasowa do t) $+$ (waga krawędzi z t do s). Jeśli l jest mniejsze niż odległość tymczasowa do s, zmień tę odległość na l i zapamiętaj t jako poprzednik s.

Łatwo pokazać, że przemieszczając się w grafie rozpoczynając z wierzchołka $v$ i poruszając się do kolejnych zapamiętanych poprzedników (aż do osiągnięcia $u$, który nie ma poprzednika), poruszamy się wstecz po najkrótszej ścieżce łączącej $u$ z $v$. Tę ścieżkę można odtworzyć odwracając kolejność przemieszczania się w sposób identyczny, jak w algorytmie przeszukiwania wszerz.

Implementacja ¶

Omówimy tu pewne szczegóły implementacji algorytmu Dijkstry z pliku dijkstra.py. Algorytm opakowujemy w klasę Dijkstra, dziedziczącą z klasy BFS, implementującą metody:

clear(self) - nadpisana metoda BFS, która wywołuje clear() z nadklasy (które to wywołanie m.in. ustawia wszystkie wierzchołki jako białe - nieodwiedzone) oraz dodatkowo nadaje wszystkim wierzchołkom nieskończoną odległość tymczasową.
dijkstra(self, start_key) - wykonuje algorytm Dijkstry na grafie podanym przy konstrukcji obiektu, rozpoczynając od wierzchołka o kluczu start_key.

Dodatkowo, klasa dziedziczy z BFS metodę traverse(self, key_x), której znaczenie i działanie jest identyczne.

Omówimy pewne szczegóły implementacji. Wewnętrznie, klasa używa do działania tych samych atrybutów, co BFS:

g - instancja grafu podana w konstruktorze. W algorytmie Dijkstry wykorzystujemy wagi krawędzi tego grafu.
colors - słownik kolorów wierzchołków (czysto kosmetyczne, zamiast kolorów można po prostu zapamiętywać zbiór wierzchołków odwiedzonych).
predecessors - słownik poprzedników odwiedzonych wierzchołków (innych niż początkowy), identycznie jak w BFS.
distances - w odróżnieniu od BFS, w tym słowniku przechowujemy odległości tymczasowe wierzchołków, początkowo nieskończone.

Nieskończoność w algorytmie reprezentujemy stałą inf z modułu math.

Kluczowym elementem algorytmu Dijkstry jest zdolność wybierania wierzchołków do odwiedzania zgodnie z ich tymczasowymi odległościami. Implementujemy ten wybór z użyciem kolejki priorytetowej. Na początku algorytmu, umieszczamy w kolejce wszystkie wierzchołki z priorytetem inf, poza początkowym, który umieszczamy w niej z priorytetem 0. Wybór wierzchołka do odwiedzenia odpowiada wyciągnięciu wierzchołka z kolejki. Relaksacja odległości tymczasowych odpowiada zmniejszeniu priorytetu w kolejce. Samą kolejkę implementujemy przez kopiec, zgodnie z opisem z poprzedniego podrozdziału: trzymamy w nim pary złożone z odległości tymczasowych wierzchołków, oraz samych wierzchołków. Najistotniejszy krok - relaksacja odległości tymczasowej (wraz z testem, czy to potrzebne) wygląda następująco:

if current_distance + weight < neighbor_distance:
                    h.decrease_key((neighbor_distance, nbr_key),
                                   (current_distance + weight, nbr_key))

Przykład - połączenia lotnicze ¶

Rozważmy takie zadanie:

Mamy samolot, który ma ograniczony zasięg.
Na świecie jest pewna ilość lotnisk, pomiędzy którymi możemy podróżować. Możliwa jest podróż pomiędzy dowolną parą lotnisk (wzdłuż koła wielkiego Ziemi, które je łączy).
Chcemy dostać się z wybranego lotniska $A$ na wybrane lotnisko $B$, niekoniecznie bezpośrednio - możemy odwiedzać inne lotniska po drodze. Nie możemy niestety podróżować pomiędzy lotniskami, których odległość przekracza zasięg naszego samolotu. Po wylądowaniu na danym lotnisku możemy jednak uzupełnić paliwo, nie mamy zatem ograniczenia na całkowitą długość trasy.
Chcemy znaleźć optymalną (najkrótszą) trasę z $A$ do $B$, minimalizując tym samym zużyte paliwo i czas.

Przykładowe dane do zadania znajdują się w pliku cities.txt. Jego pierwsza linijka to liczba $n$ - ilość miast (lotnisk). W $n$ następnych linijkach umieszczone są nazwy kolejnych miast. W dalszych $n$ linijkach, oddzielone spacjami znajduje się po $n$ liczb na linijkę. Liczba $j$-ta w $i$-tej z tych linijek reprezentuje odległość (w setkach mil) między miastami $i$ i $j$.

Ostatnie $n$ linijek jest więc macierzą sąsiedztwa grafu ważonego, w którym wierzchołkami są miasta, a wagi krawędzi to odpowiednie odległości. Jeśli z tego grafu usuniemy krawędzie dłuższe ("cięższe"), niż zasięg samolotu, wtedy problem optymalnej trasy z $A$ do $B$ tłumaczy się na znalezienie najkrótszej ścieżki pomiędzy odpowiednimi wierzchołkami w takim pomniejszonym grafie. Stąd pomysł na rozwiązanie:

Optymalna trasa między miastami A i B dla samolotu o zasięgu max_dist, kroki:

Wczytaj ilość, nazwy miast, macierz sąsiedztwa z pliku.

Skonstruuj graf (instancję Graph) z użyciem wczytanej macierzy, dodając do grafu tylko krawędzie krótsze, niż max_dist.

Wykonaj na grafie algorytm Dijsktry o początku w A.

Użyj traverse(B), aby odczytać znalezioną najkrótszą ścieżkę.

Tak opisany algorytm opakujemy w klasę CityNetwork (implementacja w city_network.py), która oprócz znajdowania najkrótszej ścieżki pozwala też formatować znalezioną ścieżkę, wypisując podstawowe informacje o odwiedzanych lotniskach i długości ścieżki.

from city_network import CityNetwork

print('Shortest Paris-Baghdad route (with capped leg distance):')
for max_dist in (8, 9, 10, 11, 15, 20, 24):
    network = CityNetwork('cities.txt', max_dist)
    print('Max distance {}: '.format(max_dist) +
          network.describe_route('Paris', 'Baghdad'))

Shortest Paris-Baghdad route (with capped leg distance):
Max distance 8: No possible route!
Max distance 9: Paris-Rome: 7, Rome-Istanbul: 9, Istanbul-Cairo: 8, Cairo-Baghdad: 8 (total: 32)
Max distance 10: Paris-Rome: 7, Rome-Istanbul: 9, Istanbul-Baghdad: 10 (total: 26)
Max distance 11: Paris-Berlin: 5, Berlin-Istanbul: 11, Istanbul-Baghdad: 10 (total: 26)
Max distance 15: Paris-Istanbul: 14, Istanbul-Baghdad: 10 (total: 24)
Max distance 20: Paris-Istanbul: 14, Istanbul-Baghdad: 10 (total: 24)
Max distance 24: Paris-Baghdad: 24 (total: 24)

Obserwujemy jak w miarę zwiększania zasięgu otwierają się nam nowe dostępne połączenia, skracając optymalną trasę, aż do dopuszczenia bezpośredniego (zatem najkrótszego) lotu między lotniskami. Podobnie:

from city_network import CityNetwork

print('Shortest Azores-Tokyo route (with capped leg distance):')
for max_dist in range(10, 100, 10):
    network = CityNetwork('cities.txt', max_dist)
    print('Max distance {}: '.format(max_dist) +
          network.describe_route('Azores', 'Tokyo'))

Shortest Azores-Tokyo route (with capped leg distance):
Max distance 10: No possible route!
Max distance 20: No possible route!
Max distance 30: No possible route!
Max distance 40: Azores-Montreal: 24, Montreal-Juneau: 26, Juneau-Tokyo: 40 (total: 90)
Max distance 50: Azores-Paris: 16, Paris-Berlin: 5, Berlin-Moscow: 10, Moscow-Tokyo: 47 (total: 78)
Max distance 60: Azores-London: 16, London-Tokyo: 60 (total: 76)
Max distance 70: Azores-London: 16, London-Tokyo: 60 (total: 76)
Max distance 80: Azores-Tokyo: 73 (total: 73)
Max distance 90: Azores-Tokyo: 73 (total: 73)