G. Jagiella

Skrypt do wykładu Programowanie 2 (Python)

ostatnia modyfikacja: 06.04.2020

Wykład 7 - grafy i algorytm BFS

Spis treści

Wstęp

Word ladder to gra wymyślona przez Lewisa Carrolla, w której ustalamy dwa legalne słowa z wybranego języka (ustalmy, że będą to słowa ze słownika języka angielskiego): słowo początkowe i słowo końcowe. Ruchem jest zmiana litery w słowie na inną w taki sposób, żeby uzyskać legalne słowo. Zadaniem jest przeprowadzenie słowa początkowego do słowa końcowego w jak najmniejszej ilości ruchów.

Przykładowo, słowo MATH można przeprowadzić na słowo CATS w dwóch ruchach: MATH → MATS → CATS. Jest to najmniejsza potrzebna ilość ruchów, bo słowo początkowe i końcowe różnią się dwoma literami. Słowa MATH i PIGS różnią się wszystkimi czterema literami, więc konieczna ilość ruchów na przeprowadzenie jednego na drugie to 4 (np. MATH → PATH → PITS → PATS → PIGS). Słowa RIGHT i WRONG różnią się wszystkimi pięcioma literami, więc minimalna ilość ruchów nie może być mniejsza od 5. Okazuje się jednak, że potrzeba co najmniej 11 ruchów, np. RIGHT → BIGHT → BIGOT → BIGOS → BIGGS → BIOGS → BROGS → BRIGS → BRINS → BRING → WRING → WRONG. Oczywiście pewnych słów nie da się w żaden sposób uzyskać z innych, na przykład gdy są one różnych długości.

Szukanie najkrótszej sekwencji ruchów, przeprowadzającej jedno słowo w drugie, to szczególny przypadek problemu poszukiwania najkrótszej scieżki. W tym rozdziale omówimy strukturę danych, której taki problem dotyczy, oraz algorytm go rozwiązujący.

Grafy

Definicja i przykłady

Grafy to uogólnienie struktur łączonych takich jak listy łączone i drzewa.

Definicja. Graf (skierowany) to para $(V, E)$, gdzie $V$ jest zbiorem, a $E$ relacją na nim.

  • Zbiór $V$ nazywamy zbiorem wierzchołków (lub węzłów) grafu.
  • Parę $(u, v) \in E$ nazywamy krawędzią z $u$ do $v$.

Definicja. Graf nieskierowany to graf $(V, E)$, w którym $E$ jest symetryczna, tzn. $\forall u, v \in V ((u,v) \in E \iff (v, u) \in E)$.

Uwaga. W ramach konwencji, na naszym wykładzie zbiór $V$ zawsze będzie skończony (tj. zajmujemy się jedynie grafami skończonymi).

Matematycznie zatem, graf jest po prostu zbiorem z relacją. Grafy możemy wizualizować, rysując diagramy tej relacji (jak na Wstępie do matematyki). W przypadku grafów nieskierowanych, zamiast rysować strzałki pomiędzy parami wierzchołków, łączymy je kreską (bez strzałek), reprezentującą obie krawędzie.

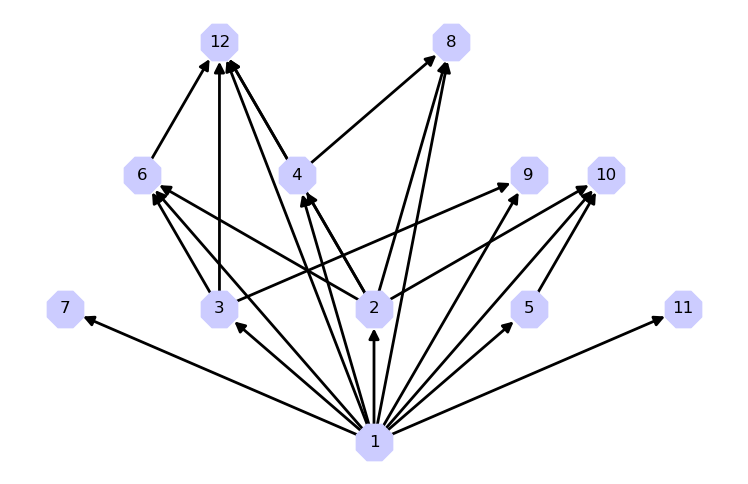
Przykład 1. Graf skierowany $G = (V, E)$, gdzie wierzchołkami są liczby, a krawędzie oznaczają podzielność:

  • $V = \{n \in \mathbb{N}_+ : n \leq 12\}$.
  • $(n,m) \in E \iff n | m \land n < m$.

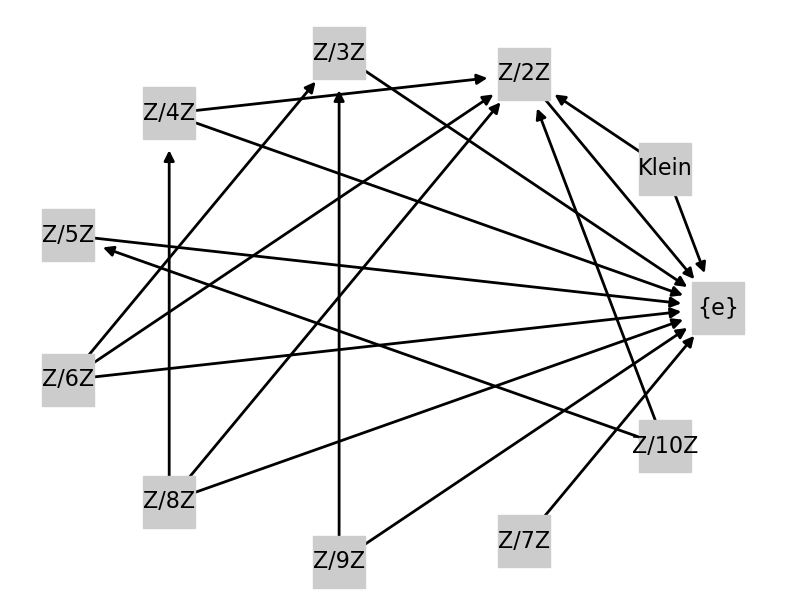
Przykład 2. Graf skierowany $G = (V, E)$, gdzie wierzchołkami są pewne grupy (w sensie algebraicznym):

  • $V = \{\mathbb{Z}/n\mathbb{Z} : 1 \leq n \leq 10 \} \cup \{Klein\}$.
  • $(g_1,g_2) \in E \iff g_1 \neq g_2 \text{ i istnieje epimorfizm } f: g_1 \to g_2$.

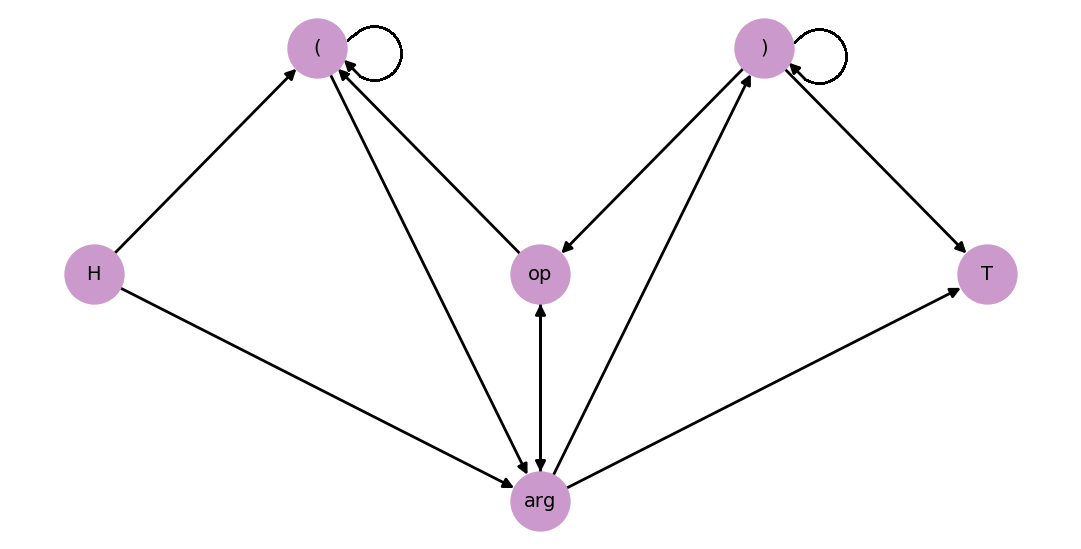
Przykład 3. Graf skierowany $G = (V, E)$, w którym wierzchołkami są typy (rodzaje) tokenów w wyrażeniach arytmetycznych w zwykłej notacji.

  • $V = \{\text{(}, \text{)}, op, arg, H, T\}$, typy tokenów.
  • $(t_1, t_2) \in E \iff \text{ token typu } t_2 \text{ może wystąpić po } t_1 \text{ w wyrażeniu infix}.$

Powyżej, $op$ i $arg$ to typy tokenów: operatorów i liczb/zmiennych odpowiednio. Natomiast $H$ i $T$ to "sztuczne" tokeny oznaczające początek (head) i koniec (tail) wyrażenia arytmetycznego. Krawędź z tokenu $H$ do tokenu $u$ oznacza, że $u$ może pojawić się na początku wyrażenia. Analogicznie, krawędź z tokenu $u$ do tokenu $T$ oznacza, że $u$ może pojawić się na końcu. Korzystając z grafu, możemy łatwo rozstrzygnąć, czy ciąg tokenów jest legalnym wyrażeniem w zwykłej notacji arytmetycznej. Dla ciągu $a_0, a_1, \ldots, a_n$ jest tak dokładnie wtedy, gdy jednocześnie:

  • dla wszystkich par $a_i, a_{i+1}$, gdzie $0 \leq i < n$, typ tokenu $a_{i}$ może (według diagramu) wystąpić przed typem tokenem $a_{i+1}$, oraz
  • wyrażenie (ciąg) jest poprawnie znawiasowane.

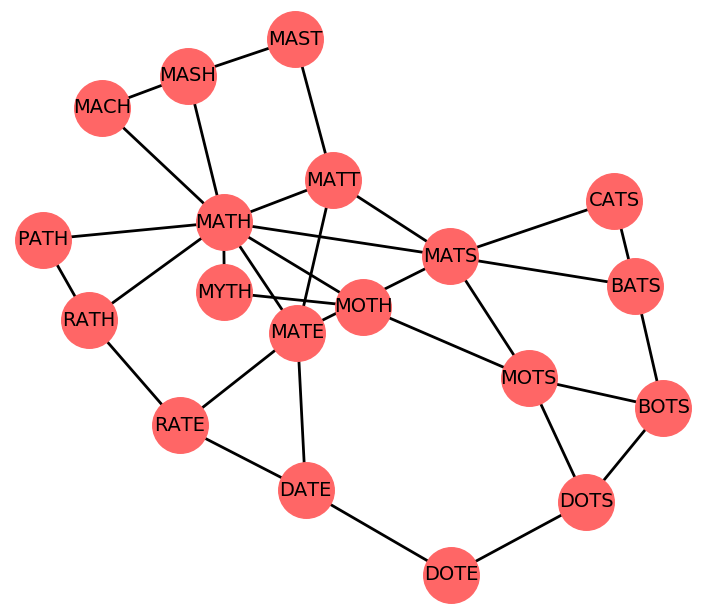
Przykład 4. Graf nieskierowany $(V, E)$ niektórych "sąsiednich" słów, jak w grze Word ladder.

  • $(w_1, w_2) \in E$ gdy słowo $w_1$ powstaje ze słowa $w_2$ przez zamianę jednej litery na inną.

Terminologia i reprezentacje grafów

Wprowadzimy teraz terminologię dotyczącą grafów. Uwaga: Niektóre z pojęć dla grafów będą inne, niż analogiczne pojęcia wprowadzone dla drzew. Zestawienie definicji i konwencji stosowanych na wykładzie (i listach zadań) znajduje się na stronie wykładu.

Niech $G = (V, E)$. Przyjmujemy nazewnictwo:

  • Jeśli $(u, v) \in E$, to $v$ nazywamy sąsiadem $u$.
  • Ścieżka (skierowana) z wierzchołka $u$ do $v$ to ciąg krawędzi $(u_1, v_1), \ldots, (u_n,v_n)$ takich, że $\forall i (v_i = u_{i+1})$, $u = u_1, v_{n} = v$.
  • Ścieżka nieskierowana z wierzchołka $u$ do $v$ to ciąg krawędzi $(u_1, v_1), \ldots, (u_n,v_n)$ takich, że $\forall i \big( \{u_i, v_i\} \cap \{u_{i+1}, v_{i+1}\} \neq \emptyset \big)$, $u \in \{u_1, v_1\}, v \in \{u_n, v_n\}$.
  • Odległość między $u$ i $v$ to długość najkrótszej ścieżki [lub ścieżki nieskierowanej] z $u$ do $v$, jeśli taka istnieje. W przeciwnym wypadku jako odległość kładziemy $\infty$.

Przyjmujemy też, że każdy wierzchołek $v$ jest połączony sam ze sobą pustą ścieżką. Odległość z $v$ do $v$ wynosi $0$.

W grafach (w tym również drzewach) jako definicję ścieżki przyjmuje się często ciąg krawędzi wraz z kolejnymi wierzchołkami występującymi na ścieżce.

Przyjrzymy się teraz bliżej zdefiniowanemu powyżej pojęciu odległości i umotywujemy ją przy użyciu teorii przestrzeni metrycznych. Pojęcie odległości można rozważać w dwóch wariantach:

  • Dla ścieżek skierowanych (odległość skierowana), lub
  • Dla ścieżek nieskierowanych (odległość nieskierowana).

Zauważamy, że w grafach nieskierowanych oba warianty się pokrywają.

Niech teraz $d \colon V \times V \to \mathbb{R} \cup \{\infty\}$ będzie funkcją zdefiniowaną przez $$d(x, y) = \text{ odległość nieskierowana z } x \text{ do } y.$$ Zwracamy uwagę, że $d$ przyjmuje jedynie wartości naturalne i $\infty$.

Fakt. Dla wszystkich $x, y, z \in V$:

  1. $d(x, y) = 0 \iff x = y$,
  2. $d(x, y) = d(y, x)$,
  3. $d(x, z) \leq d(x, y) + d(y, z)$.

Dowód. 1. Jedynym wierzchołkiem w odległości $0$ od siebie samego jest on sam. 2. wynika wprost z faktu, że gdy ciąg krawędzi $e_1, e_2, \ldots, e_n$ jest nieskierowaną ścieżką z $x$ do $y$, to ciąg $e_n, e_{n-1}, \ldots, e_1$ jest nieskierowaną scieżką z $y$ do $x$ tej samej długości. 3. Nierówność może nie zajść jedynie wówczas, gdy prawa strona jest skończona, czyli gdy $d(x, y) = n$ i $d(y, z) = m$ dla pewnych $n, m \in \mathbb{N}$. To oznacza, że istnieją nieskierowane ścieżki: z $x$ do $y$ długości $n$ oraz z $y$ do $z$ długości $m$. Połączenie tych ścieżek jest ścieżką nieskierowaną z $x$ do $z$ długości $n + m$, która zaświadcza, że $d(x, z) \leq n+m$.

Fakt mówi więc, że funkcje $d$ spełnia wszystkie aksjomaty metryki (identyczność elementów w odległości $0$, symetryczność, oraz nierówność trójkąta). Jedynym - pozornym - problemem jest, że $d$ może przyjmować wartości nieskończone. Nie jest to jednak prawdziwy problem: metryki w ogólności można bez przeszkód definiować jako funkcje w $\mathbb{R} \cup \{\infty\}$ i cała teoria i terminologia przestrzeni metrycznych (kule otwarte i domknięte etc.) przenosi się do tego kontekstu.

Traktując $d$ jako metrykę, w naturalny sposób pojawiają się w kontekście grafów pojęcia kul (o zadanym środku i promieniu), średnicy etc. Mają one sens również w sytuacji, gdy graf $(V, E)$ jest nieskończony.

Uwaga 1. Zwracamy uwagę, że graf to "jedynie" zbiór z relacją, i już ta relacja indukuje na zbiorze strukturę przestrzeni metrycznej.
Uwaga 2. Odległość skierowana spełnia aksjomaty 1. i 3. z Faktu, jednak dla grafów, które nie są nieskierowane, aksjomat 2. zawodzi.

Omówimy teraz sposoby reprezentacji grafów. Założymy teraz, że wierzchołki grafu numerowane są (kolejnymi) dodatnimi liczbami naturalnymi, $V = \{1, 2, \ldots, n\}$.

Mamy następujące, elementarne sposoby reprezentowania grafów:

I. Listy sąsiedztwa. W tym sposobie, dla każdego wierzchołka $i = 1, \ldots, n$ pamiętamy listę (lub zbiór, słownik) złożony z tych wierzchołków, które są sąsiadami $i$. Złożoność pamięciowa tego rozwiązania to $\Theta(|E| + |V|)$, gdyż list jest tyle, ile wierzchołków, a elementów list w sumie dokładnie tyle, co krawędzi.

II. Macierze sąsiedztwa. Definiujemy macierz $n \times n$ postaci $\{a_{i,j}\}_{1 \leq i, j \leq n}$, gdzie $a_{i,j} = 1$, gdy $(i,j) \in E$ i $0$ w przeciwnym przypadku. Złożoność pamięciowa to rozmiar macierzy, czyli $\Theta(|V|^2)$.

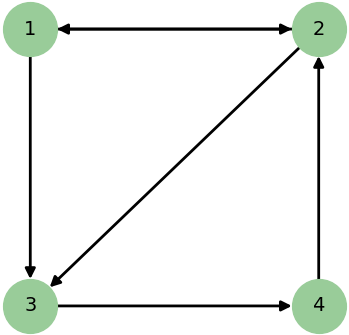
Przykład 5. Dany jest następujący graf:

Jego reprezentacja przy użyciu list sąsiedztwa jest następująca:

1: [2, 3]
2: [1, 3]
3: [4]
4: [2]

Natomiast przy użyciu macierzy sąsiedztwa: $$\{a_{i,j}\} = \begin{pmatrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \end{pmatrix} $$

Grafy ważone i ich reprezentacje

Grafy ważone to takie grafy, w których każda krawędź ma przypisaną tzw. wagę. Wagi takie mogą na przykład reprezentować odległości między miastami (gdzie miasta to wierzchołki), lub koszt zmiany stanu z jednego na drugi (gdzie stany to wierzchołki). Formalnie:

Definicja Graf ważony to trójka $(V, E, f)$, gdzie $(V, E)$ jest grafem, a $f : E \to \mathbb{R}$ jest funkcją nadającą wagi krawędziom.

Uwaga. Wagi mogą być liczbami ujemnymi. Waga $0$ nie oznacza braku krawędzi.

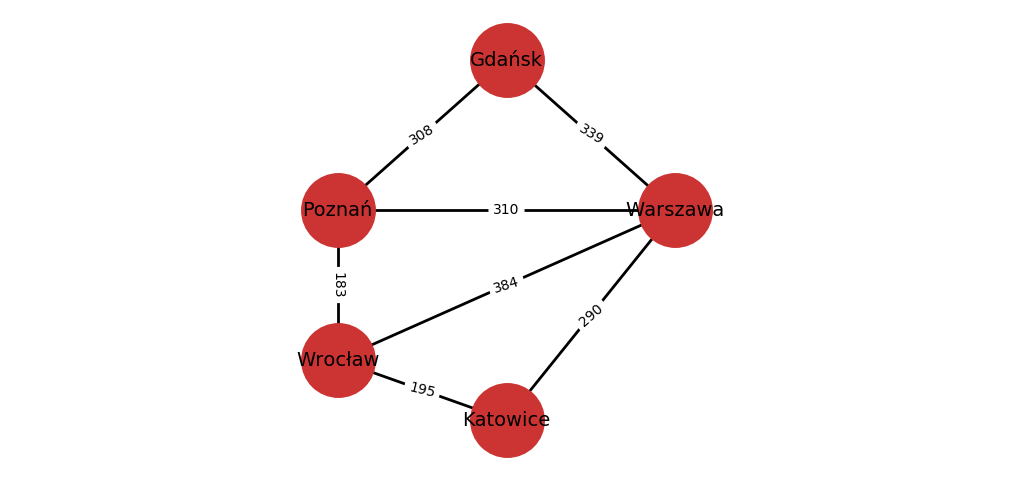
Przykład 6. Graf odległości między niektórymi dużymi miastami w Polsce.

Uwaga. Dla grafów ważonych, musimy być staranni stosując pojęcie grafu nieskierowanego. Możemy bowiem mieć do czynienia z grafem ważonym $(V, E, f)$, gdzie $(V, E)$ jest nieskierowany ($E$ jest symetryczna), ale dla pewnej pary wierzchołków $u, v \in V$ połączonych krawędzią mamy $f((u,v)) \neq f((v,u))$. W Przykładzie 6 mamy graf nieskierowany, w którym wagi odpowiednich par krawędzi są takie same. Możemy jednak reprezentować jako graf połączenia między miastami (wierzchołkami), w których połączenia są symetryczne, a wagi to czasy pokonania tych połączeń. Czasy te nie muszą być takie same dla obu kierunków.

Elementarne sposoby reprezentacja grafów ważonych są podobne, jak dla grafów bez wag. Ponownie załóżmy, że wierzchołki grafów to kolejne liczby naturalne dodatnie.

I. Słowniki sąsiedztwa. Dla każdego wierzchołka $i = 1, \ldots, n$ pamiętamy słownik, w którym kluczami są wierzchołki, które są sąsiadami $i$, a wartościami wagi krawędzi prowadzących do tych sąsiadów.

II. Macierze sąsiedztwa. Definiujemy macierz $n \times n$ postaci $\{a_{i,j}\}_{1 \leq i, j \leq n}$, gdzie $a_{i,j} = f((i,j))$, gdy $(i, j) \in E$. Gdy $(i, j) \notin E$, nie definiujemy współczynnika $a_{i,j}$ (w Pythonie możemy użyć None do reprezentowania braku tej wartości).

Przykład 7. Dla grafu z Przykładu 6 powyżej, gdzie Gdańsk, Poznań, Warszawa, Wrocław, Katowice to odpowiednio wierzchołki $1, 2, 3, 4, 5$.

Reprezentacja przy użyciu słowników sąsiedztwa jest następująca:

1: {2: 308, 3: 339}
2: {1: 308, 3: 310, 4: 183}
3: {1: 339, 2: 310, 4: 384, 5: 290}
4: {2: 183, 3: 384, 5: 195}
5: {3: 290, 4: 195}

Natomiast przy użyciu macierzy sąsiedztwa: $$\{a_{i,j}\} = \begin{pmatrix} & 308 & 339 & & \\ 308 & & 310 & 183 & \\ 339 & 310 & & 384 & 290 \\ & 183 & 384 & & 195 \\ & & 290 & 195 & \end{pmatrix} $$ gdzie brak współczynnika nie jest tożsamy z $0$.

Implementacja

Zaimplementujemy grafy jako obiektowy wariant słowników sąsiedztwa. Wierzchołki każdego grafu będą identyfikowane przez unikalne klucze (identyfikatory). Graf zawsze będzie ważony - grafy bez wag możemy reprezentować jako grafy ważone, w których każdą wagą jest $1$. Stworzymy klasy:

  1. Vertex, reprezentującą pojedynczy wierzchołek grafu. Będzie przechowywał swój klucz oraz słownik połączeń z innymi wierzchołkami.
  2. Graph, reprezentującą cały graf, z operacjami dodawania nowych wierzchołków oraz krawędzi.

Dalsze szczegóły interfejsów obu klas:

  1. Klasa Vertex będzie zawierać metody:
    • __init__(self, key) - tworzy nowy wierzchołek o kluczu key.
    • get_id(self) - zwraca klucz (identyfikator) self.
    • add_neighbor(self, nbr, weight=1) - dodaje sąsiada nbr, gdzie nbr jest wierzchołkiem (obiektem typu Vertex, nie jego kluczem) połączonego z self krawędzią o wadze weight.
    • get_connections(self) - zwraca iterowalny obiekt złożony z sąsiadów self.
    • get_weight(self, nbr) - zwraca wagę połączenia z sąsiadem nbr, gdzie nbr to Vertex.
    • __str__(self) - zwraca reprezentację wierzchołka jako napis.
  1. Klasa Graph, używająca klasy Vertex, będzie implementować metody:
    • __init__(self) - tworzy nowy, pusty graf.
    • add_vertex(self, key) - tworzy nowy wierzchołek o podanym kluczu key i dodaje go do grafu. key nie powinien być kluczem wierzchołka, który jest już w grafie.
    • get_vertex(self, key) - zwraca obiekt Vertex, wierzchołek o kluczu key. Zwraca None, jeśli takiego wierzchołka nie ma.
    • add_edge(self, f, t, weight=1) - dodaje krawędź między wierzchołkami o kluczach f i t o wadze cost. Jeśli dowolny z tych wierzchołków nie istnieje, zostanie stworzony i dodany do grafu.
    • get_vertices(self) - zwraca obiekt iterowalny złożony z wierzchołków self
    • __contains__(self, key) - implementuje operator in: sprawdza, czy wierzchołek o kluczu key znajduje się w grafie.
    • __iter__(self) - zwraca iterator, przebiegający po wierzchołkach (obiektach Vertex) grafu.

Implementacje klas znajdują się w plikach vertex.py i graph.py. Ich przykładowe użycie:

In [1]:
from graph import Graph

# Tworzymy graf, dodajemy wierzchołki 0, 1, 2, 3, 4, 5:
g = Graph()
for i in range(6):
    g.add_vertex(i)

# Dodajemy niektóre krawędzie (z wagą domyślną 1):
g.add_edge(0, 1)
g.add_edge(0, 5)
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(3, 4)
g.add_edge(3, 5)
g.add_edge(4, 0)
g.add_edge(5, 4)
g.add_edge(5, 2)

# Iterujemy po wierzchołkach g, każdy wypisujemy:
for v in g:
    print(v)

0 connected to: [1, 5].
1 connected to: [2].
2 connected to: [3].
3 connected to: [4, 5].
4 connected to: [0].
5 connected to: [4, 2].

Przeszukiwanie wszerz

Opis

Omówimy teraz algorytm BFS (breadth-first search, algorytm przeszukiwania wszerz), który trawersuje (odwiedza) wierzchołki grafu skierowanego rozpoczynając od pewnego ustalonego wierzchołka ("źródła"), odwiedzając wszystkie wierzchołki, które są połączone ze źródłem skierowaną ścieżką. Wierzchołki będą odwiedzane w kolejności o najbliższych do najdalszych źródłowemu, zaczynając od samego źródła. Następnie zmodyfikujemy go tak, aby trawersując graf zapamiętywać odległości odwiedzonych wierzchołków wraz z informacją wystarczającą do odtworzenia najkrótszej ścieżki prowadzącej od źródła do tego wierzchołka (czyli ścieżki zaświadczającej o jego odległości od źródła).

Idea algorytmu jest prosta - najpierw odwiedzamy źródło. Następnie odwiedzamy (w dowolnej kolejności) wszystkie sąsiady źródła. Następnie odwiedzamy sąsiady sąsiadów źródła, które nie są sąsiadami źródła (czyli nie zostały już odwiedzone). W kolejnych krokach odwiedzamy sąsiady sąsiadów ... sąsiadów źródła, które nie zostały już wcześniej odwiedzone. Naszym celem będzie teraz takie sformalizowanie algorytmu, które pomoże w jego efektywnej (i wydajnej czasowo) implementacji.

W opisie algorytmu będziemy wykorzystywać następujące koncepty:

  • Wierzchołkom będą nadawane kolory: biały, szary i czarny.
  • Białe wierzchołki będą odkrywane: ich kolor zmieni się wtedy na szary.
  • Szare, odkryte wierzchołki, będą odwiedzane, zmieniając kolor na czarny.

Każdy wierzchołek w grafie jest początkowo biały. Każdy wierzchołek może zostać odkryty co najwyżej raz, a każdy odkryty wierzchołek zostanie ostatecznie odwiedzony.

W algorytmie będziemy używać (początkowo pustej) kolejki. Odkrycie wierzchołka będzie tożsame z położeniem go w kolejce (i pokolorowaniem go na szaro). Wierzchołki położone do kolejki zostaną z później niej wyciągnięte - zostaną wtedy odwiedzone (i pokolorowane na czarno).

Kroki algorytmu BFS, wersja pierwsza (gdzie $t_0$ - wierzchołek źródłowy):

  1. Stwórz pustą kolejkę $q$.
  2. Oznacz $t_0$ jako odkryty i umieść go na końcu $q$.
  3. Dopóki $q$ jest niepusta:
    3a. Weź wierzchołek $t$ z początku kolejki.
    3b. Oznacz nieodwiedzone, nieodkryte sąsiady $t$ jako odkryte i umieść je na końcu $q$.
    3c. Oznacz $t$ jako odwiedzony.

Poniższa animacja ilustruje działanie algorytmu dla grafu zbudowanego na koniec poprzedniej sekcji, gdzie wierzchołkiem początkowym jest 0. Na czerwono podświetlany jest aktualny węzeł odwiedzany w algorytmie ($t$), krawędzie prowadzące do jego sąsiadów, oraz jego kolejne sąsiady obsługiwane w kroku 3b. Oprócz stanu kolejki (każdy umieszczony w niej wierzchołek jest szary), pokazujemy w jaśniejszym kolorze te wierzchołki, które już zostały z niej wyciągnięte:

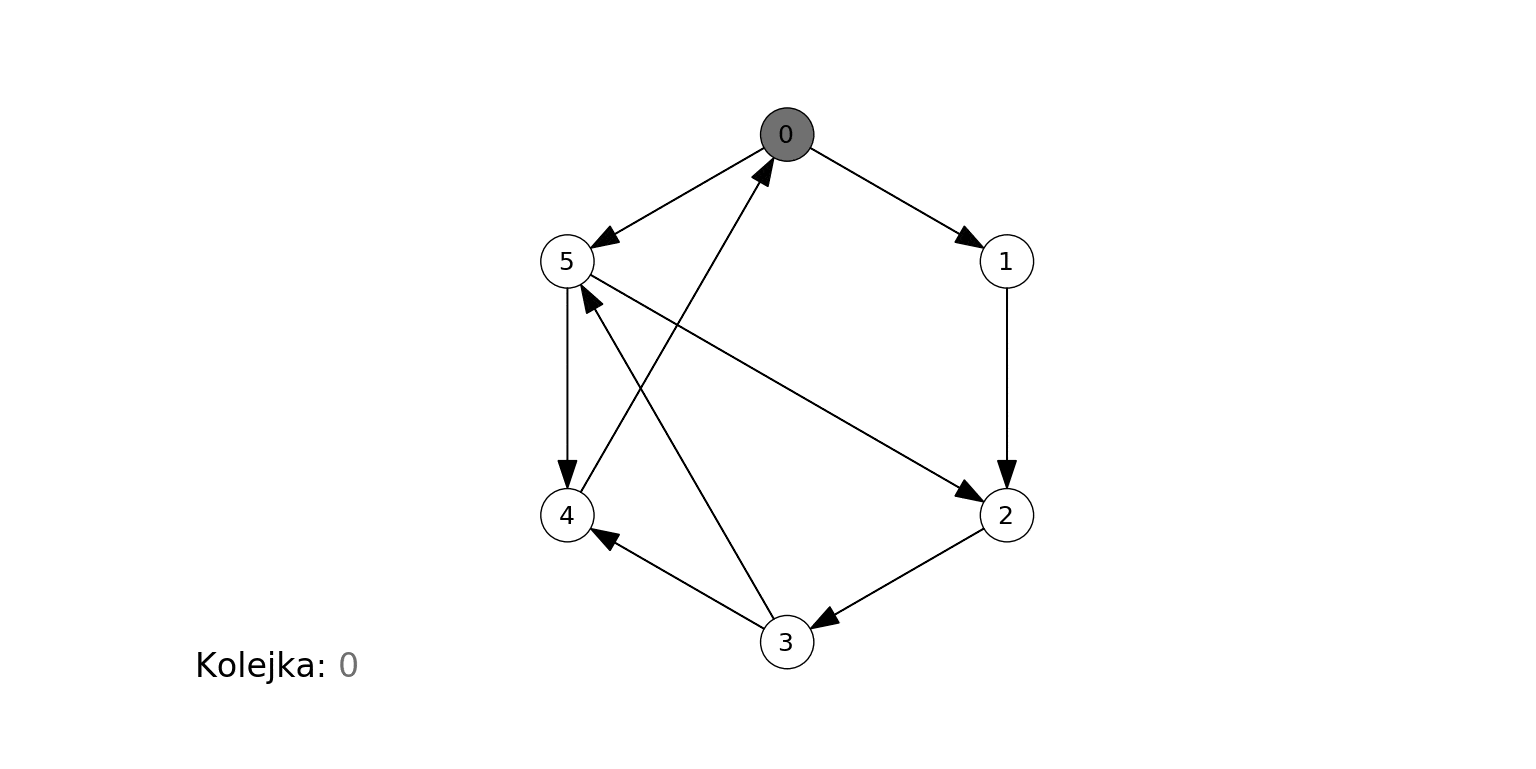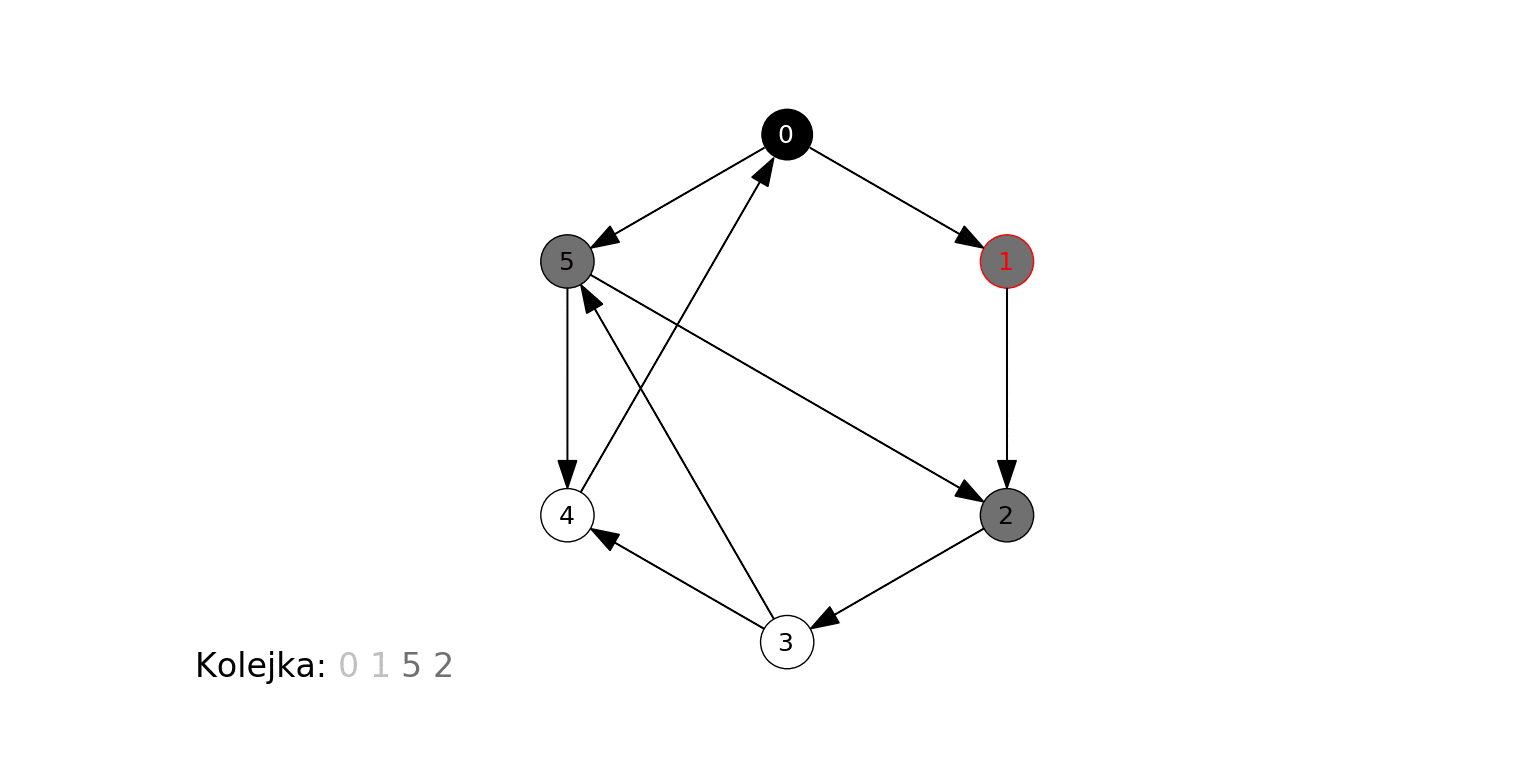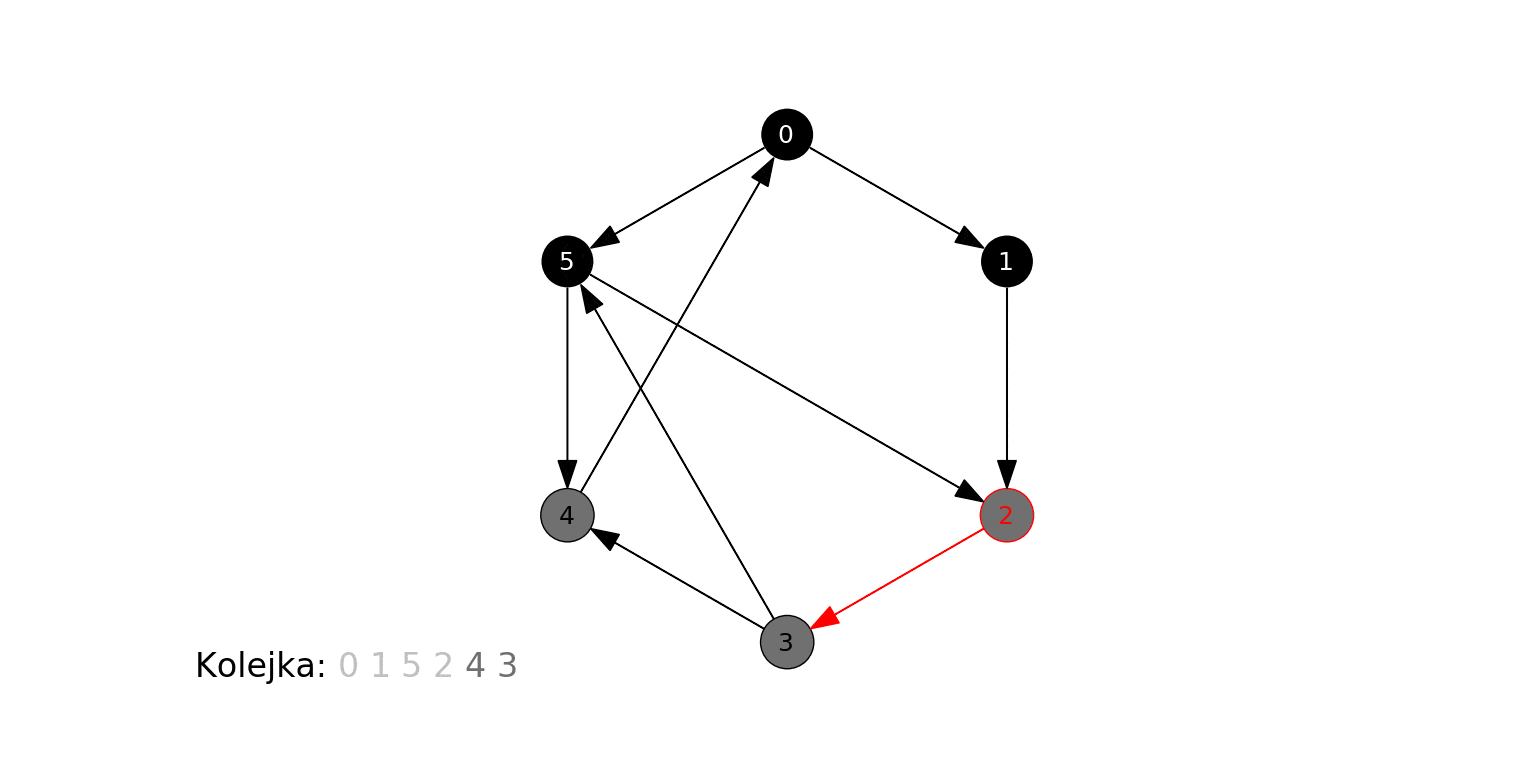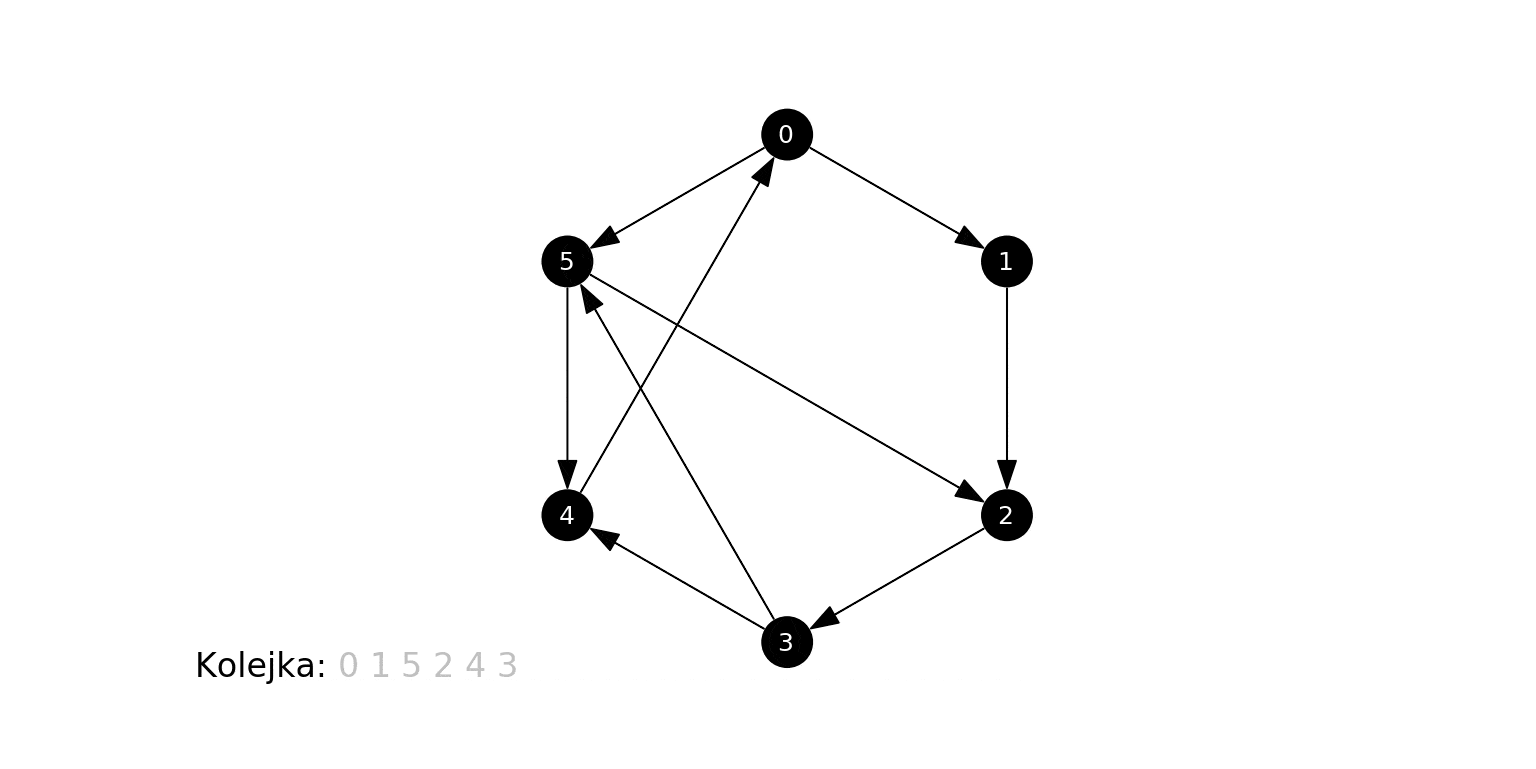
Algorytm odkrył, a następnie odwiedził wierzchołki w kolejności 0, 1, 5, 2, 4, 3.

  • 0 jest samym źródłem.
  • 1 i 5 są w odległości 1 od źródła.
  • 2 i 4 są w odległości 2 od źródła.
  • 3 jest w odległości 3 od źródła.

Poniżej działanie algorytmu na losowo wygenerowanym grafie. Zwracamy uwagę, że algorytm odkrył i odwiedził jedynie wierzchołki "osiągalne" z ze źródła przez skierowaną ścieżkę. Zbiór takich wierzchołków (i krawędzi między nimi) to tzw. silna spójna składowa danego wierzchołka (tu: źródła).

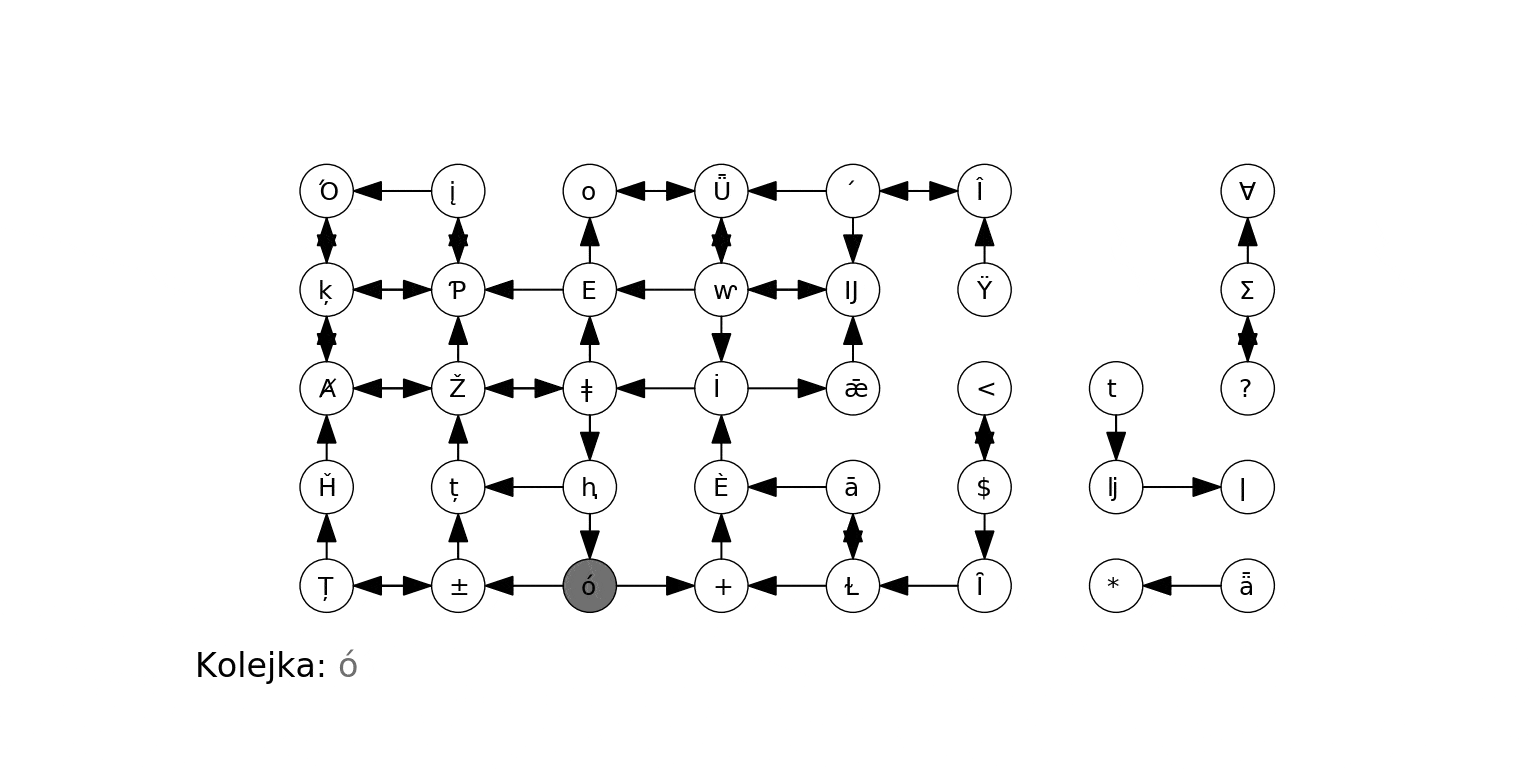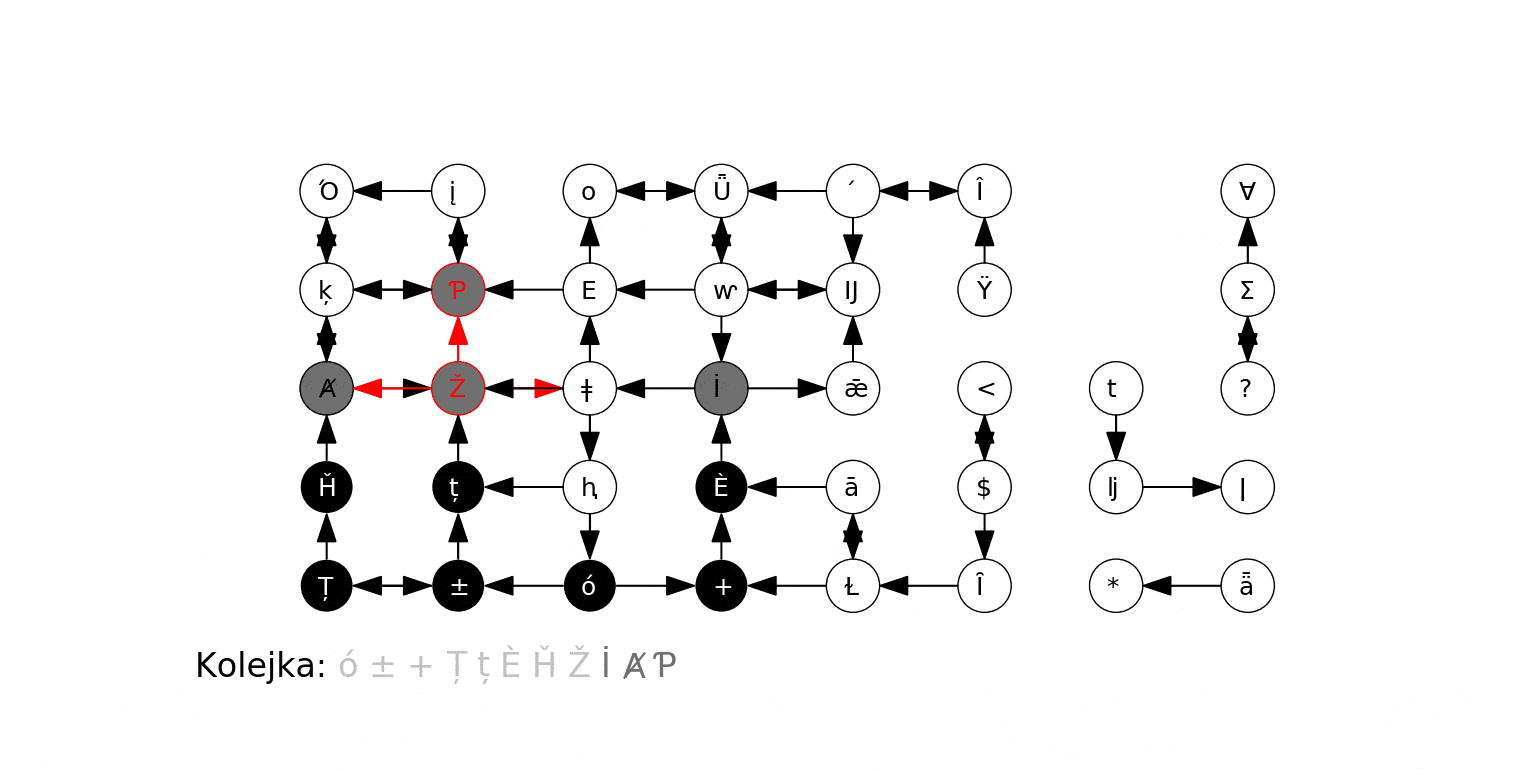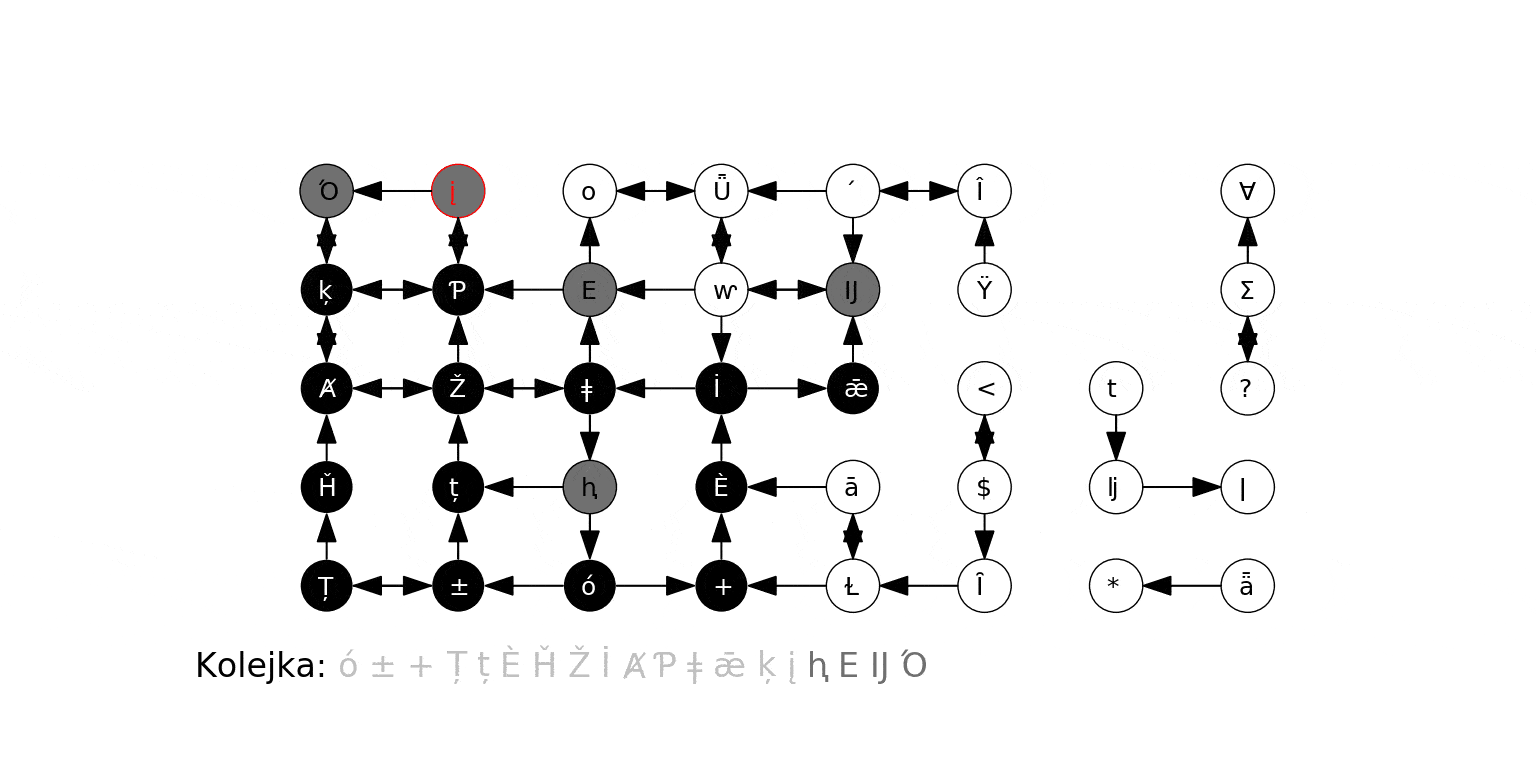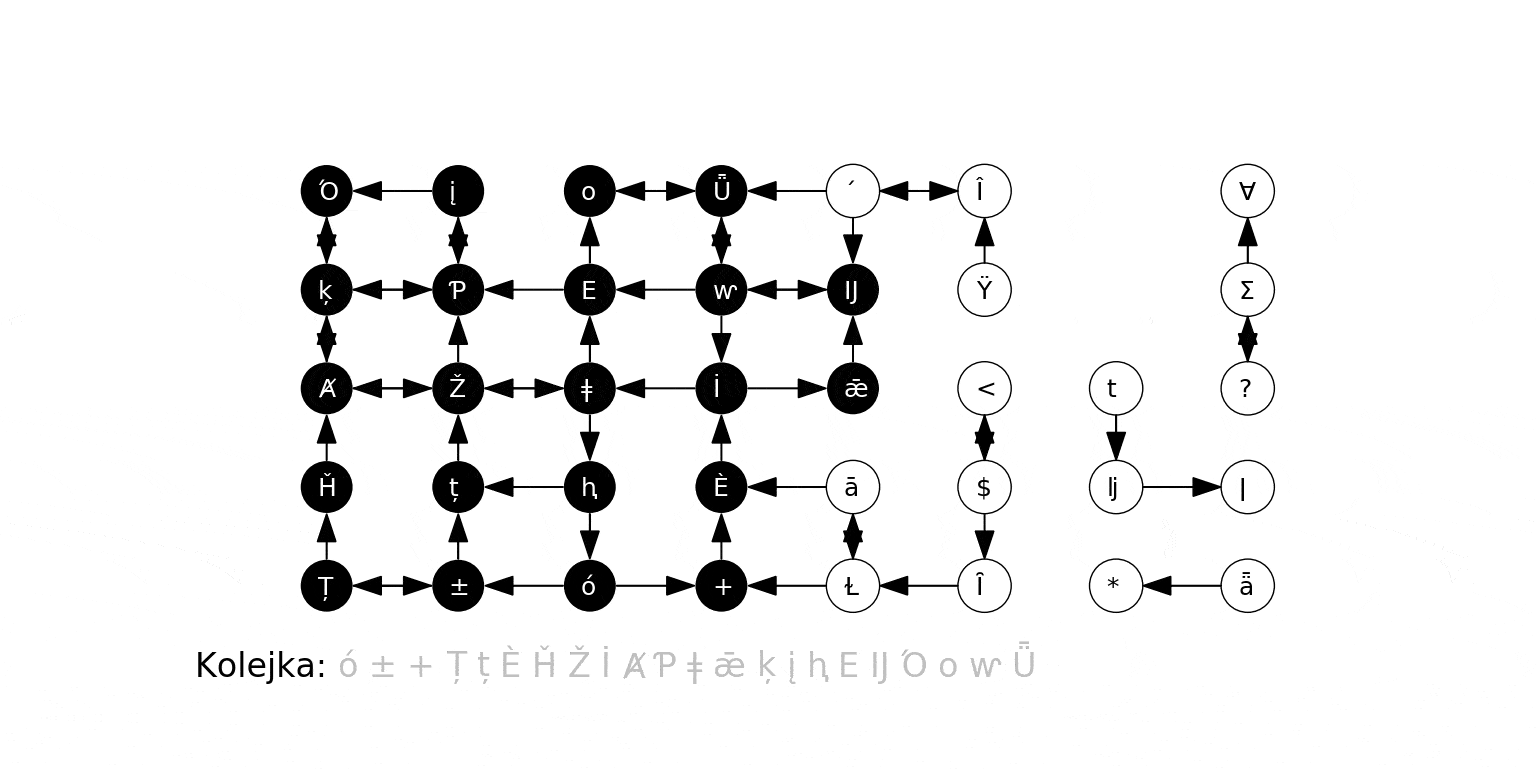
Wreszcie działanie na "kompletnym" grafie podobnym do powyższego:

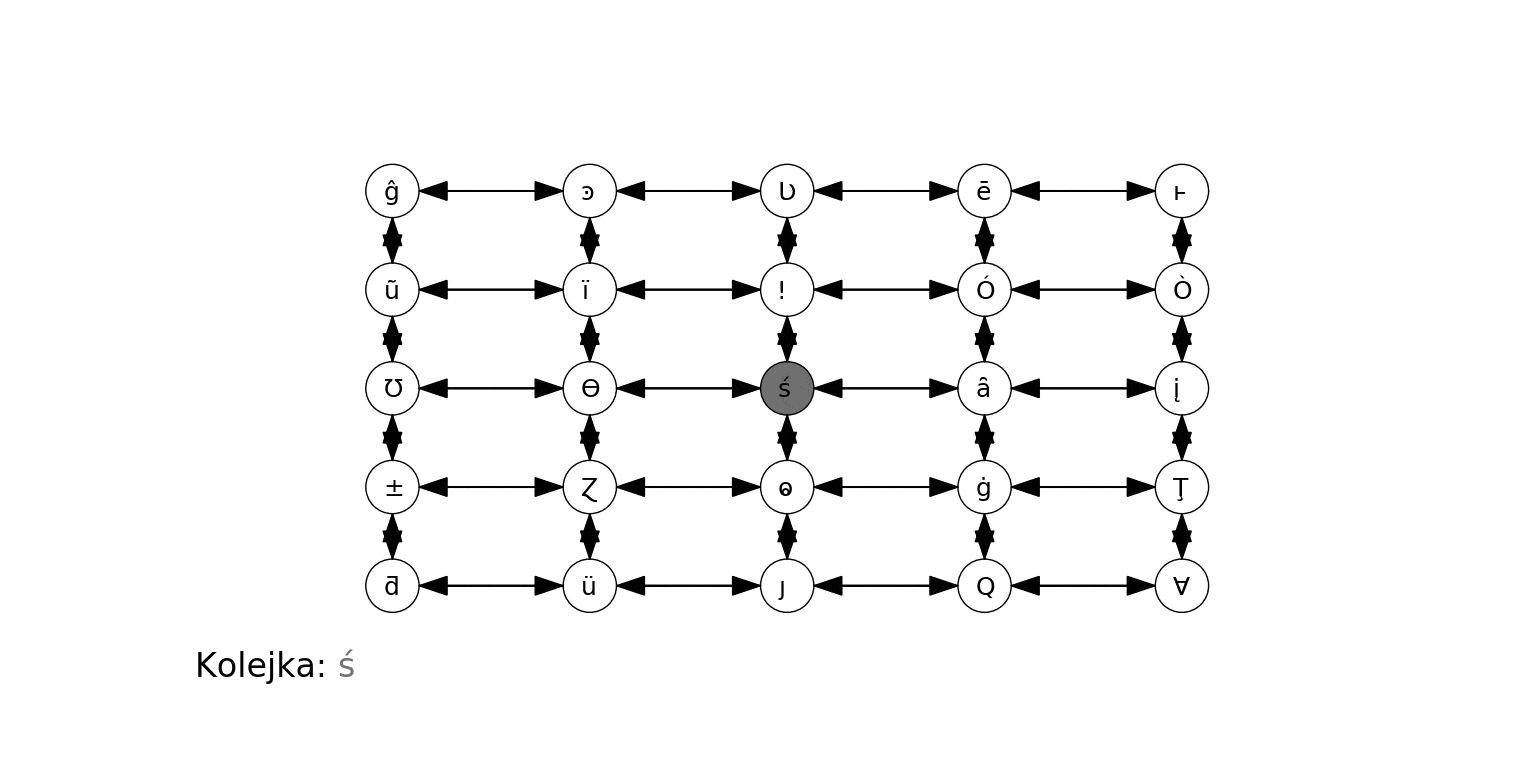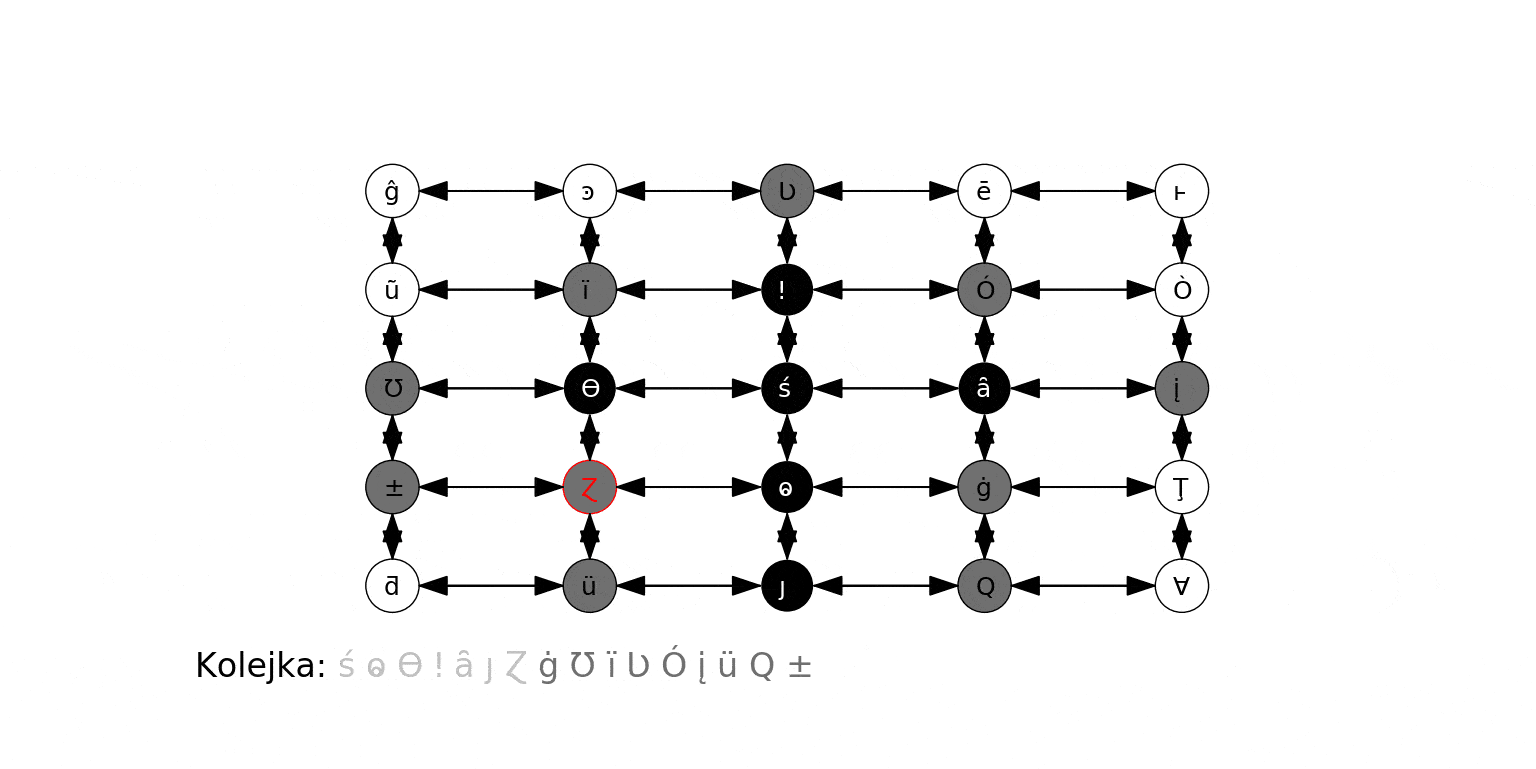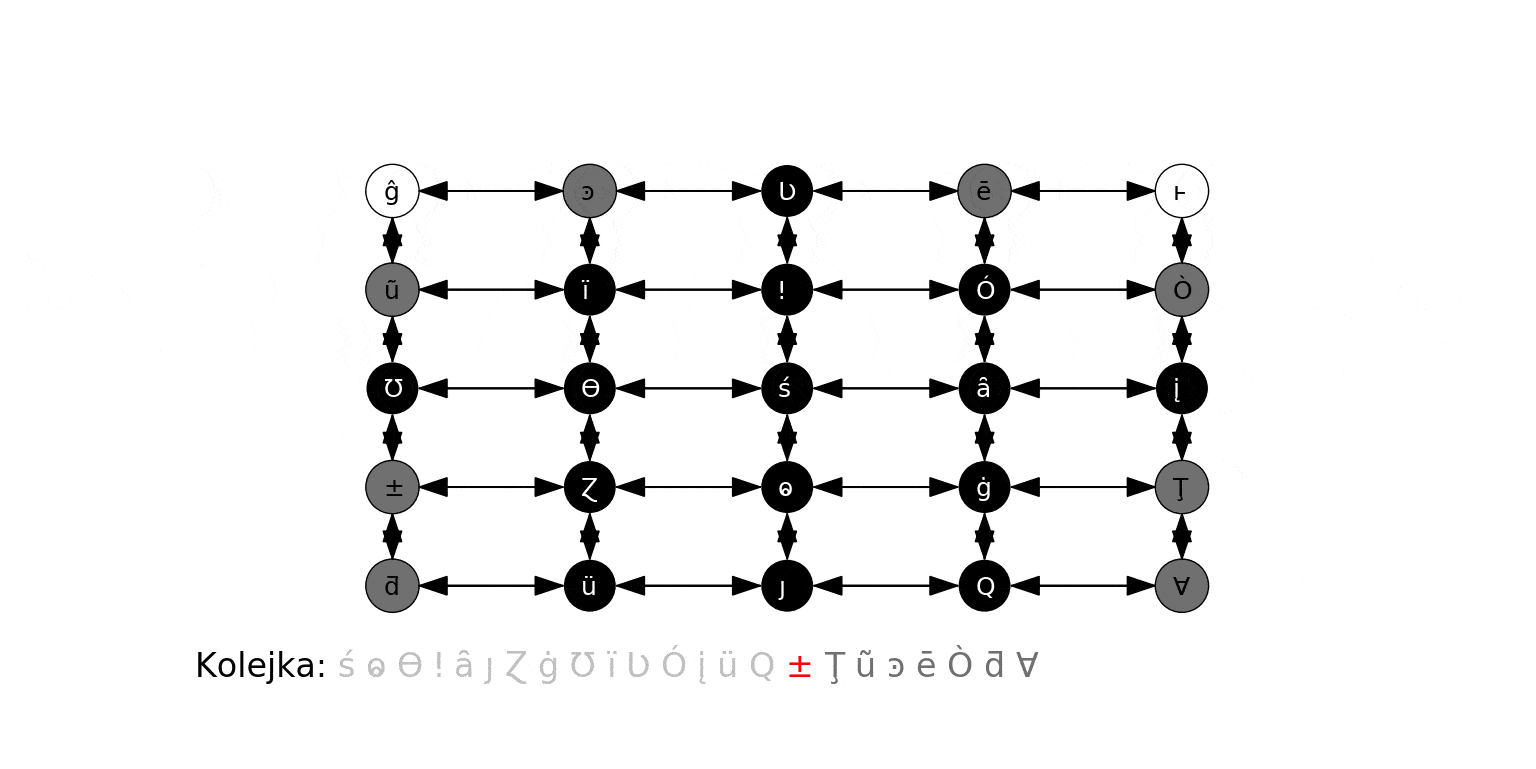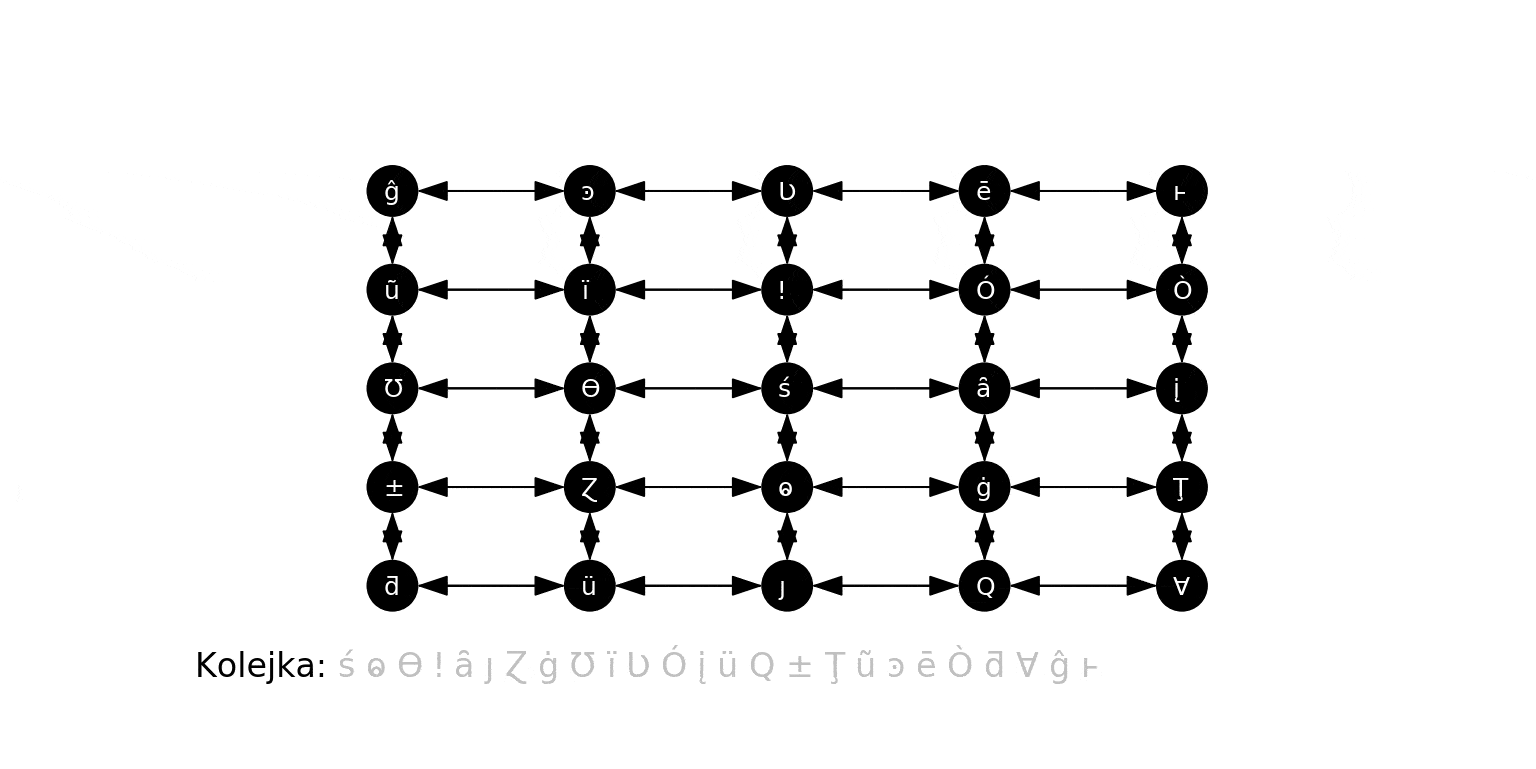
Uzasadnimy teraz formalnie, dlaczego algorytm BFS rozpoczęty w $t_0$ rzeczywiście odwiedza wierzchołki silnej składowej spójności $t_0$ w kolejności ich odległości (skierowanej) od $t_0$. Dla grafu $G = (V,E)$ wprowadźmy oznaczenia:

  • $B(x, n)$: zbiór wierzchołków $G$ odległych od $x$ o mniej niż $n$.
  • $S(x, n)$: zbiór wierzchołków $G$ w odległości dokładnie $n$ od $x$.

Intuicyjnie: $B(x,n)$ to kula otwarta o środku w $x$ i promieniu $n$ według "niesymetrycznej metryki" zadanej przez skierowaną odległość między wierzchołkami. Podobnie, $S(x,n)$ to odpowienia sfera.

Fakt. Wierzchołek jest odkryty dokładnie wtedy, gdy czeka w kolejce na odwiedzenie (lub gdy jest właśnie odwiedzany).

Poczyńmy też trywialną obserwację (z warunku trójkąta):

Fakt. Jeśli $t \in V$ leży w odległości $m$ od $t_0$, to każdy sąsiad $t$ leży w odległości co najwyżej $m+1$ od $t_0$.

Pokażemy teraz:

Stwierdzenie. Dla każdego $n \in \mathbb{N}$, istnieje krok BFS, w którym jednocześnie:

  1. Zbiór wierzchołków odwiedzonych to $B(t_0, n)$,
  2. Zbiór wierzchołków odkrytych to $S(t_0, n)$. Dowód. Prowadzimy indukcję względem $n$. Dla $n=0$ odpowiedni krok następuje, gdy odkrywamy $t_0$ na samym początku algorytmu ($B(t_0, 0)$ jest pusty, $S(t_0, 0) = \{t_0\}$). Załóżmy teraz, że warunki 1. i 2. zachodzą dla pewnego $n > 0$. Są dwa przypadki:
  3. Jeśli $S(t_0, n)$ jest pusty, to kolejka wierzchołków odkrytych jest pusta i algorytm kończy działanie. Wtedy $B(t_0, n) = B(t_0, n+1) = \ldots$ składa się ze wszystkich wierzchołków osiągalnych z $t_0$ ścieżką skierowaną i wszystkie te wierzchołki są odwiedzone.
  4. Jeśli $S(t_0, n)$ jest niepusty, to jego elementy są dokładnie elementami (niepustej) kolejki wierzchołków. Rozważmy krok uzyskany odwiedzeniu ich wszystkich. Po pierwsze, zbiorem odwiedzonych wierzchołków jest wtedy $B(t_0, n) \cup S(t_0, n) = B(t_0, n+1).$ Niech $S$ będzie zbiorem wierzchołków odkrytych. Każdy wierzchołek $t \in S$ został odkryty podczas odwiedzania wierzchołków $S(t_0, n)$, więc jest sąsiadem co najmniej jednego z nich - stąd jego odległość od $t_0$ jest nie większa od $n+1$. Z drugiej strony, $x$ nie został odkryty wcześniej, czyli $x \notin B(t_0, n+1)$. Stąd $S \subseteq S(t_0, n+1)$. Z drugiej strony, każdy element $S(t_0, n+1)$ jest sąsiadem co najmniej jednego wierzchołka z $S(t_0, n)$, zatem został odkryty. Stąd $S = S(t_0, n+1)$. $\dashv$

Wniosek. Algorytm BFS odwiedza $t_0$ a następnie kolejno wierzchołki z $S(t_0, 1), S(t_0, 2), \ldots$ aż do wyczerpania wierzchołków w skończonej odległości od $t_0$. Kolejność odwiedzania wierzchołków w każdym ze zbiorów $S(t_0, n)$ (czyli równoodległych od $t_0$) nie musi być ustalona.

Wykorzystajmy teraz obserwację, że odkrywając wierzchołek $s$ w trakcie odwiedzania wierzchołka $t$ mamy pewność, że odległość $s$ od $t_0$ jest o dokładnie jeden większa, niż odległość $t$ od $t_0$. Zmodyfikujmy algorytm BFS tak, aby dla kolejno odkrywanych wierzchołków zapamiętywać tę odległość, wraz z wierzchołkiem, z którego go odkryliśmy.

Kroki algorytmu BFS, wersja druga (gdzie $t_0$ - wierzchołek źródłowy):

  1. Stwórz pustą kolejkę $q$.
  2. Oznacz $t_0$ jako odkryty i umieść go na końcu $q$.
  3. Nadaj $t_0$ odległość $0$.
  4. Dopóki $q$ jest niepusta:
    4a. Weź wierzchołek $t$ z początku kolejki.
    4b. Niech $n$ = odległość nadana $t$.
    4c. Oznacz nieodwiedzone, nieodkryte sąsiady $t$ jako odkryte i umieść je na końcu $q$. Nadaj im odległość $n+1$. Zapamiętaj, że są sąsiadami $t$.
    4d. Oznacz $t$ jako odwiedzony.

Zobaczmy teraz działanie tego ulepszonego algorytmu na pierwszym grafie, na którym badaliśmy zachowanie BFS (źródłem jest wierzchołek 0). Obok każdego wierzchołka w nawiasie pojawia się nadana mu odległość, a dla oznaczenia wierzchołka, z którego dany wierzchołek został odkryty (jego "poprzednika") rysujemy żółtą krawędź:

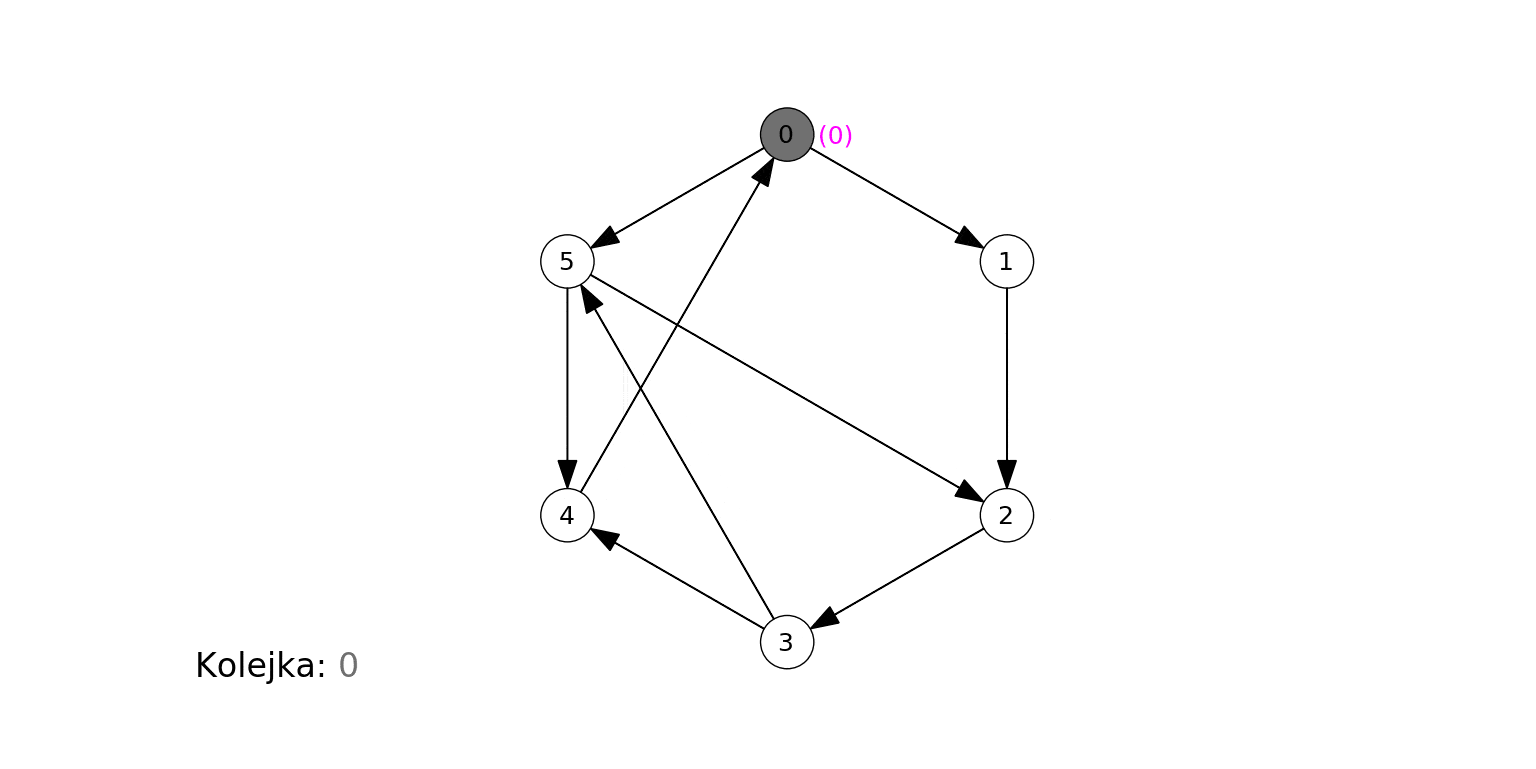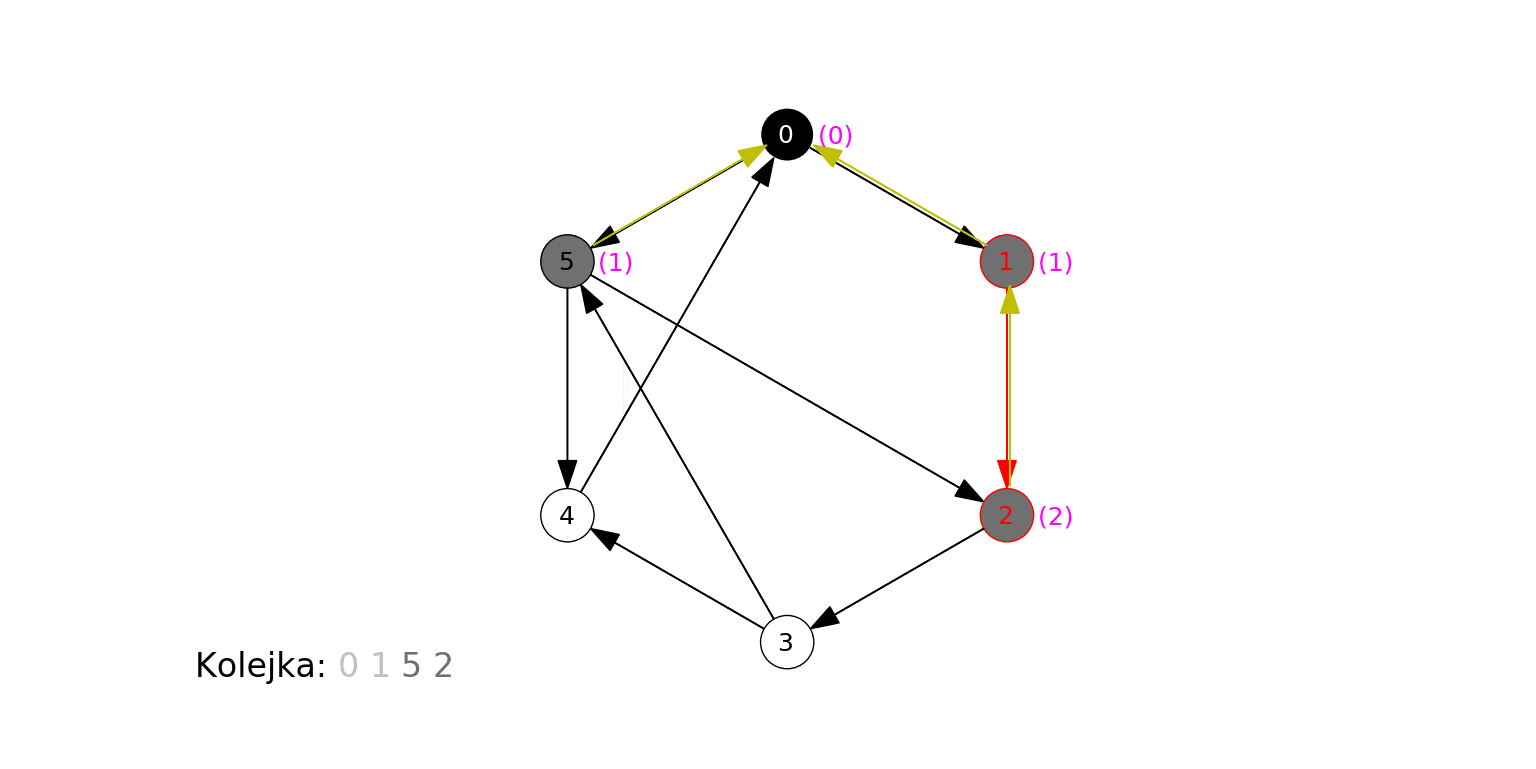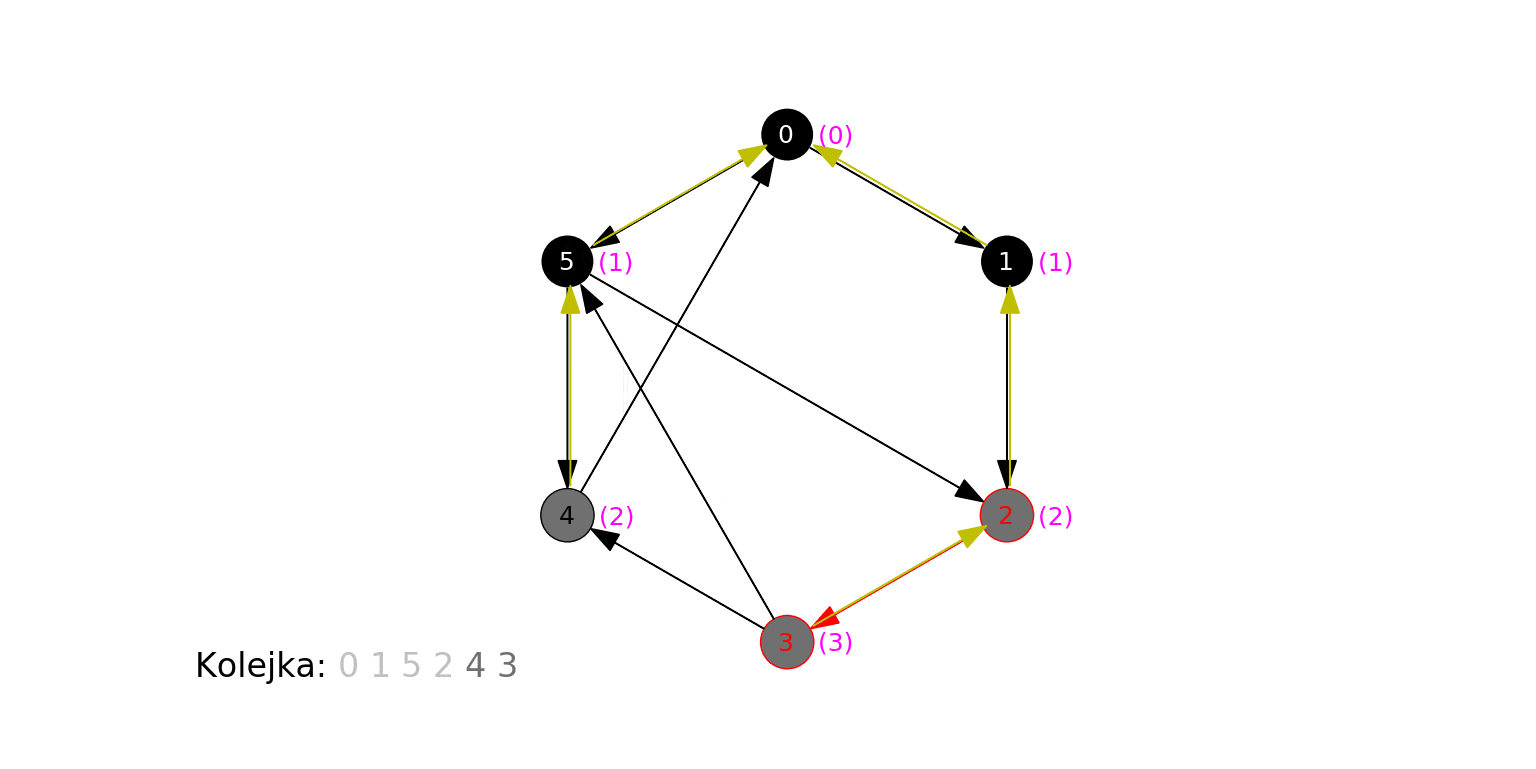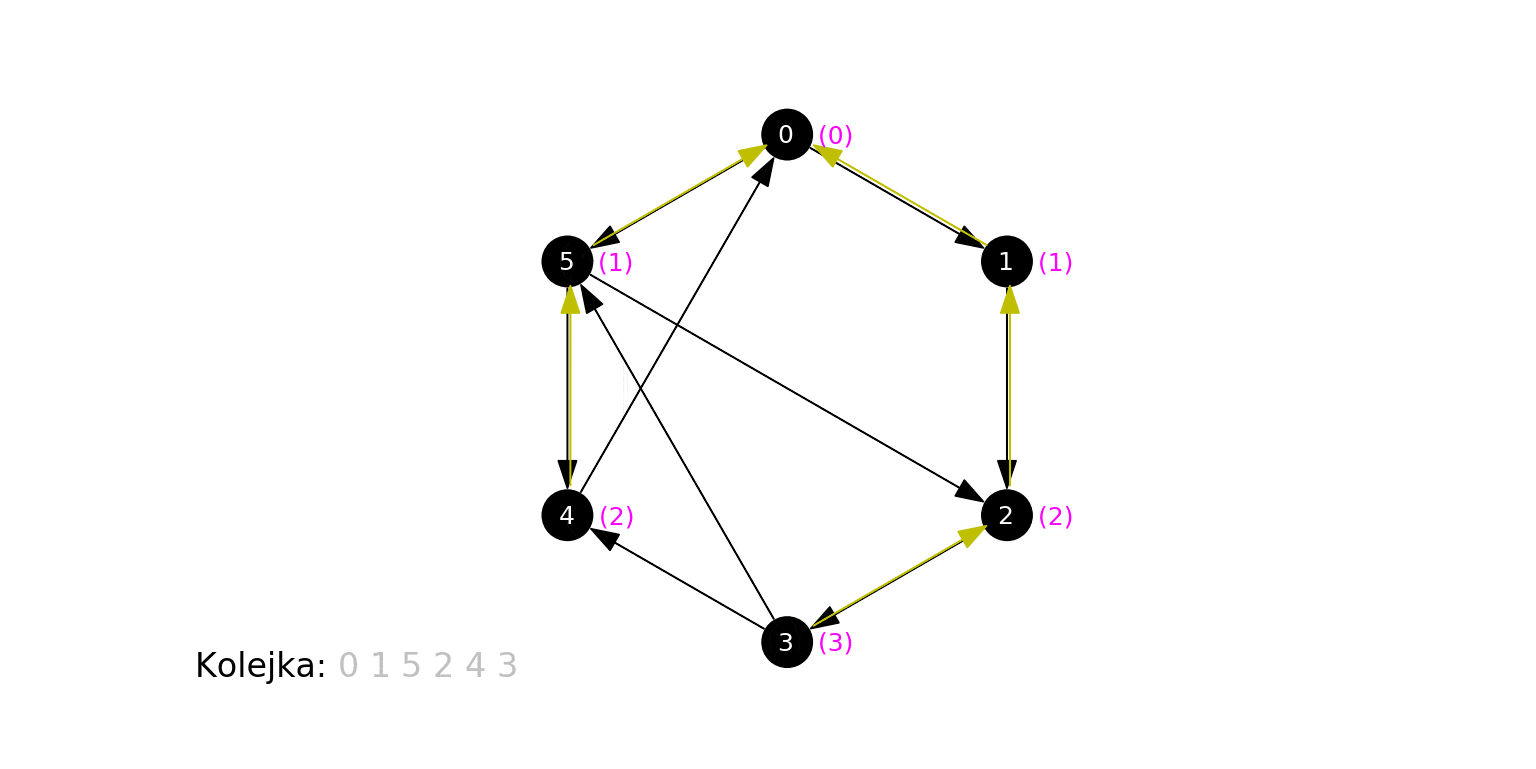
Spójrzmy na ostatni krok animacji - stan po zakończeniu działania algorytmu:

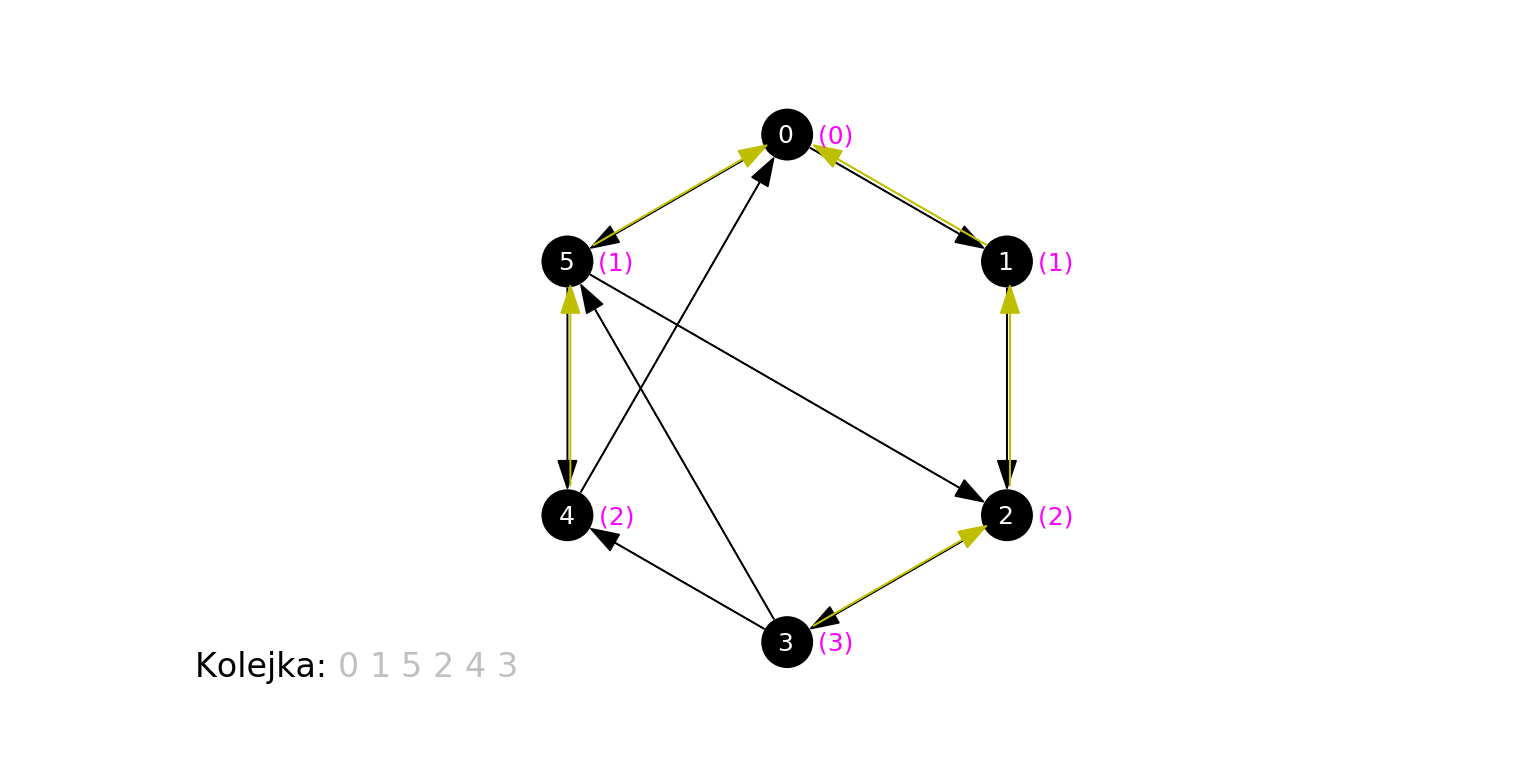
Każdemu wierzchołkowi została poprawnie przypisana jego odległość od źródła, oraz wierzchołek "poprzednik", którego jest sąsiadem, który to poprzednik jest o $1$ bliższy źródłowemu (wyjątkiem jest źródło, dla którego takiego wierzchołka nie ma).

Zapamiętanie "poprzednika" pozwala nam na skuteczne znalezienie najkrótszej ścieżki, prowadzącej od źródła do wybranego wierzchołka. Aby zrekonstruować ścieżkę, wystarczy podążać w kierunku "poprzedników" aż dojdziemy do źródła. Odczytane tak wierzchołki, w odwrotnej kolejności, leżą na (koniecznie najkrótszej) ścieżce prowadzącej od źródła do wierzchołka. Przykładowo, na rysunku powyżej, żółte strzałki wskazują, że 3 jest sąsiadem 2, które jest sąsiadem 1, które jest sąsiadem 0. Stąd najkrótsza ścieżka od 0 do 3 składa się z krawędzi (0, 1), (1, 2) i (2, 3).

Złożoność BFS

Niech $G=(V,E)$ będzie grafem, na którym przeprowadzamy BFS (druga wersja) począwszy w $t_0$ o którym zakładamy, że da się z niego poprowadzić ścieżkę do każdego wierzchołka $V$ (czyli BFS odwiedzi wszystkie wierzchołki $V$). Aby podać złożoność algorytmu BFS, rozważmy operacje, jakie wykonujemy na wierzchołkach. Wszystkie operacje polegające na zapamiętaniu ich poprzedników, odległości i kolorów można wykonać w czasie stałym (używając np. słowników).

  • Kroki 1-3 wykonują się raz: czas stały.
  • Kroki 4a, 4b i 4d zajmują czas stały i wykonują się raz dla każdego odwiedzonego wierzchołka, czyli $|V|$ razy.
  • Kroki podjęte dla sąsiadów wierzchołków w 4c wymagają stałego czasu. Zwracamy przy tym uwagę, że krok podjęty dla sąsiada prowadzi do jego odkrycia tylko raz. Sąsiad taki będzie jednak przetestowany (gdy sprawdzamy, czy jest odwiedzony, czy nie) za każdym razem, gdy odwiedzamy wierzchołek, z którego prowadzi do niego krawędź. Tych testów będzie więc tyle, ile krawędzi w grafie, $|E|$.

Stąd złożoność algorytmu to $\Theta(|V| + |E|)$. Ponieważ zakładamy, że wszystkie wierzchołki grafu są połączone z $t_0$, konieczne jest, że $|E| \geq |V| - 1$. Możemy więc - w tym przypadku - wyrazić czas działania jako $\Theta(|V|)$.

Jeżeli nie założymy, że każdy wierzchołek w grafie jest połączony ze źródłem, podobna analiza prowadzi do ograniczenia $O(|V| + |E|)$.

Implementacja BFS

Zaimplementujemy algorytm przeszukiwania wszerz opakowując go w klasę BFS. Konstruując obiekt typu BFS będziemy podawać konkretny graf. Następnie na takim obiekcie będziemy mogli wywoływać algorytm BFS zaczynając od wybranego wierzchołka-źródła. Algorytm ten wyliczy odległości między wszystkimi wierzchołkami a podanym źródłem oraz "poprzedniki" wszystkich tych węzłów, zapamiętując je jako atrybuty obiektu. Następnie tak skontruowany wynik algorytmu można będzie zapytywać o najkrótsze ścieżki pomiędzy źródłem, a zadanymi wierzchołkami.

Klasa BFS ma następujący interfejs:

  • __init__(self, g) - tworzy instancję BFS dla zadanego grafu g (obiektu typu Graph).
  • bfs(self, start_key) - wykonuje BFS na grafie podanym w konstruktorze, zaczynając od wierzchołka o kluczu start_key.
  • traverse(self, key_x) - zwraca listę kolejnych (kluczy) wierzchołków występujących na najkrótszej ścieżce z wierzchołka o kluczu start_key do wierzchołka o podanym kluczu key_x. Jeśli ścieżki nie ma, zwraca listę złożoną wyłącznie z key_x. Metoda wymaga, aby wcześniej została wykonana metoda bfs().

Pełna BFS implementacja znajduje się w pliku bfs.py. Skomentujemy tu pewne jej szczegóły:

  • Kolory wierzchołków, ich poprzedniki oraz zapamiętane odległości wyznaczone przez BFS trzymamy w słownikach. Początkowe, domyślne wartości dla każdego wierzchołka to odpowiednio biały kolor, odległość, brak poprzednika i odległość $0$. Wartości te są ustawiane na początku bfs() (wewnętrzna metoda clear()).
  • Jako kolejki, nie używamy klasy Queue z modułu my_queue. Ta implementacja kolejki nie była bowiem wydajna: dodawanie elementu do kolejki odbywało się w czasie liniowym. Zamiast tego, używamy deque ze standardowego modułu collections. deque to tzw. kolejka dwustronna (double-ended queue, stąd skrót). Pozwala na dokładanie i wyciąganie elementów z dwóch stron (lewej i prawej) w czasie stałym. Wewnętrznie jest zaimplementowana jako lista dwukierunkowa. Jej metody append() i popleft() mogą być użyte w chrakterze operacji enqueue i dequeue odpowiednio.
  • W metodzie traverse(), używamy stosu (własnego, Stack z modułu stack) do odwrócenia kolejności wierzchołków, gdy znajdujemy ścieżkę między wierzchołkami rekonstruowaną z poprzedników.
  • Kolory wierzchołków notujemy w słowniku colors, jako napisy, jednak jedyne miejsce, w którym je odczytujemy to początek pętli przebiegającej przez sąsiady odwiedzanego wierzchołka:
    for nbr in current_vert.get_connections():
              nbr_key = nbr.get_id()
              if self.colors[nbr_key] == 'white':
                  ...
    Zwróćmy uwagę, że test ten można uprościć: zamiast pamiętać kolory wierzchołków, wystarczyłoby zapamiętywać (w pewnym zbiorze) te, które zostały co najmniej odkryte. Następnie zmienić test na kolor na test przynależności do tego zbioru. Ta zmiana pozytywnie wpłynie na prędkość algorytmu - śledzenie kolorów wierzchołków jest wyłącznie kosmetyczne.

Użyjmy teraz BFS na grafie z przykładu:

In [3]:
from bfs import BFS

g = Graph()
for i in range(6):
    g.add_vertex(i)

g.add_edge(0, 1)
g.add_edge(0, 5)
g.add_edge(1, 2)
g.add_edge(2, 3)
g.add_edge(3, 4)
g.add_edge(3, 5)
g.add_edge(4, 0)
g.add_edge(5, 4)
g.add_edge(5, 2)

bfs = BFS(g)
bfs.bfs(0)
for v_key in g.vert_list:
    print("Path from 0 to {}: {}.".format(v_key, bfs.traverse(v_key)))

Path from 0 to 0: [0].
Path from 0 to 1: [0, 1].
Path from 0 to 2: [0, 1, 2].
Path from 0 to 3: [0, 1, 2, 3].
Path from 0 to 4: [0, 5, 4].
Path from 0 to 5: [0, 5].

Rozwiązanie Word ladder

Rozwiążemy teraz grę Lewisa Carrolla. Zauważmy, że sekwencja ruchów prowadząca z danego słowa $w_1$ do słowa $w_2$ odpowiada ścieżce prowadzącej z $w_1$ do $w_2$ w grafie jak w Przykładzie 4 poprzedniej sekcji (w którym wierzchołkami są wszystkie legalne słowa). Znalezienie pewnej (w sensie: "jakiejś") najkrótszej sekwencji ruchów jest zatem tożsame ze znalezieniem pewnej najkrótszej ścieżki między tym słowami-wierzchołkami.

Dość proste rozwiązanie problemu byłoby zatem takie:

Kroki rozwiązania Word ladder dla słów $w_1, w_2$:

  1. Zbuduj graf reprezentujący ruchy dla wszystkich leglnych słów.
  2. Wykonaj BFS o początku w $w_1$.
  3. Odczytaj najkrótszą ścieżkę prowadzącą do $w_2$.

Mamy już narzędzia do wykonania 2. i 3., pozostaje kwestia zbudowania grafu z kroku 1.

Ustalmy, skąd będziemy brać legalne słowa. Ograniczmy się - dla wydajności prezentacji - jedynie do słów czteroliterowych. Będą pochodzić z pliku slowa.txt, zawierającego czteroliterowe słowa popularnego słownika legalnych słów angielskiej wersji gry Scrabble.

Naiwnym sposobem zbudowania grafu byłoby wypełnienie go wierzchołkami oznaczającymi słowa, a następnie, dla każdej pary wierzchołków, sprawdzenie czy powinny być połączone (obustronnie) krawędziami przez zbadanie, czy róznią się dokładnie jedną literą. Par takich jest jednak kwadratowo wiele względem ilości słów.

Użyjemy wydajniejszej metody: utworzymy listy - "kubełki", z których każdy ma nazwę powstałą z zastąpienia w pewnym słowie jednej z jego liter "blankiem". Każde słowo umieszczamy w "pasujących kubełkach. Nowe kubełki tworzymy dopiero, gdy będą potrzebne.

Przykładowo, słowo MATH umieścimy w kubełkach: _ATH, M_TH, MA_H i MAT_, gdzie _ reprezentuje "blank".

Kubełki reprezentujemy jako wartości w słowniku, którego kluczami są nazwy kubełków. Dla każdego słowa z slowa.txt, tworzymy cztery nazwy kubełków, do których ono pasuje, i umieszczamy je w tych kubełkach (tworząc najpierw pusty kubełek, jeśli jeszcze taki nie istniał). Gdy skończymy, każdy kubełek zawierać będzie wszystkie słowa, które do niego pasują, np.:

  • Kubełek _ATH: ['BATH', 'EATH', 'GATH', 'HATH', 'LATH', 'MATH', 'OATH', 'PATH', 'RATH', 'TATH']
  • Kubełek MAT_: ['MATE', 'MATH', 'MATS', 'MATT', 'MATY']
  • Kubełek CAT_: ['CATE', 'CATS']

Kubełki takie tworzymy nie więcej niż po cztery na słowo (a gdyby nie ograniczać się do słów czteroliterowych, nie więcej niż ilość liter w najdłuższym słowie w języku), każde słowo dokładamy do kubełka raz. Zatem czas potrzebny na wyprodukowanie tego zestawu kubełków jest liniowo zależny od ilości słów.

Zaobserwujmy teraz, że dwa (różne) słowa w grafie powinny zostać połączone dokładnie wtedy, gdy różnią się jedną literą, czyli dokładnie wtedy, gdy leżą w jednym kubełku. Zatem wystarczy, że (dla każdego kubełka), połączymy krawędziami wszystkie pary różnych słów z danego kubełka.

Jeśli kubełki, które uzyskamy w algorytmie oznaczymy jako $A_i$ dla $i = 1, \ldots, n$, a rozmiar kubełka $A_i$ przez $|A_i|$, to przebiegnięcie przez wszystkie pary różnych słów w każdym z kubełków to $\sum_{i=1}^n{|A_i|^2}$. Zaobserwujmy jednak, że każdy kubełek jest ograniczonego rozmiaru: słów może w nim być nie więcej, niż liter, które można wstawić jako "blank", czyli - dla alfabetu angielskiego - $26$. Skoro czas "obsługi" pojedynczego kubełka jest ograniczony, a kubełków jest liniowo wiele w porównaniu do ilości słów, ten sposób generowania grafu połączeń wymaga jedynie liniowej ilości operacji w zależności od ilości słów w pliku.

Sposób "kubełkowy" jest zatem lepszy w sensie asymptotycznym. Wypada też znacznie lepiej w przykładowych testach (na średniej klasy sprzęcie i dla pliku slowa.txt):

  • Sposób kubełkowy: ~ 0.077 s
  • Sposób naiwny: ~ 23.723 s

Różnica to dwa rzędy wielkości.

Tak opisany algorytm - konstrukcję grafu na podstawie słów z pliku, a następnie BFS wyznaczający drogę dla pary wierzchołków - opakowujemy w klasę WordLadder z następującym, minimalistycznym interfejsem:

  • __init__(self, filename) - tworzy "rozwiązywacz" Word ladder dla legalnych słów pochodzących z pliku o nazwie filename. Słowa muszą w nim być rozdzielone białymi znakami.
  • shortest_path(self, word1, word2) wykonuje BFS dla słowa word1 i zwraca najkrótszą sekwencję ruchów, prowadzącą do word2 (o ile taka istnieje).

Implementacja - bardzo bezpośrednia - znajduje się w pliku word_ladder.py. Przykładowe użycie:

In [4]:
from word_ladder import WordLadder

w_ladder = WordLadder("slowa.txt")
print(w_ladder.shortest_path("MATH", "CATS"))
print(w_ladder.shortest_path("LOOP", "BUOY"))

['MATH', 'MATS', 'CATS']
['LOOP', 'LOOK', 'BOOK', 'BORK', 'BURK', 'BURY', 'BUOY']

Ćwiczenie dla czytelnika. Zmodyfikować BFS w taki sposób, aby zwracał iterator podający odwiedzane (lub odkrywane) wierzchołki, i użyć go do usprawnienia Word ladder, aby zamiast przeglądać cały graf, zakończyć algorytm już wtedy, gdy znajdziemy drogę do szukanego słowa.