wyklad6

Niech $V$ będzie skończonym zbiorem węzłów z relacją $S$. Gdy dla węzłów $x, y$, zachodzi $x S y$ mówimy, że $y$ jest dzieckiem $x$. Wprowadzamy następujące terminy:

Rodzicem węzła $x$ nazywamy węzeł $y$ taki, że $x$ jest dzieckiem $y$.
Korzeń to węzeł, który nie ma rodzica.
Liść to węzeł, który nie ma żadnego dziecka.
O węźle mówimy, że jest wewnętrzny, gdy nie jest liściem.
Ścieżka z węzła $x$ do $y$ to ciąg węzłów $x = x_1, x_2, \ldots, x_n = y$ taki, że $x_1 S x_2 S \ldots S x_n$.
Jeśli istnieje ścieżka z $x$ do $y$, to $x$ nazywamy przodkiem $y$, a $y$ potomkiem $x$. Każdy węzeł jest swoim własnym potomkiem i przodkiem.

Definicja. Para $(V, S)$ jest drzewem, gdy spełnia następujące warunki:

W $V$ jest dokładnie jeden korzeń $r$.

Dla każdego węzła $x \in V$ istnieje dokładnie jedna ścieżka z $r$ do $x$.

Wprost z definicji wynika, że jeśli $(V,S)$ jest drzewem, to każdy węzeł z $V$ z wyjątkiem korzenia posiada dokładnie jednego rodzica.

Uwaga (lingwistyczna). Rzeczowniki z terminologii powyżej odmieniamy jako nieosobowe: jedno dziecko, ale dwa dziecka (nie: "dwoje dzieci"), podobnie jak np. reprezentanty (nie: "reprezentanci") klas abstrakcji.

Poniżej kilka przykładów użycia drzew do reprezentacji różnych danych:

Przykład 1. Szczególny rodzaj drzewa genealogicznego, w którym za wierzchołki przyjmujemy wybranych potomków osoby w linii zgodnej z płcią tej osoby:

Przykład 2. Struktura katalogów na dysku (bardzo niepełny obraz):

Przykład 3. Drzewa filogenetyczne - diagramy [najbliższych] wspólnych przodków:

Źródło obrazu: Wikipedia.org, na licencji Creative Commons

Drzewa zazwyczaj rysujemy korzeniem do góry - liście umieszczamy na dole (przykład 3 powyżej jest wyjątkiem).

Uwaga 1. Są różne sposoby formalizowania drzew. Nasza formalizacja wyróżnia korzeń: w matematyce, drzewa z wyróżnionym korzeniem nazywa się ukorzenionymi. Rozważa się też drzewa nieukorzenione, w których relacja $S$ jest symetryczna. Przyjmuje się też często, że drzewo może być puste.
Uwaga 2. Przyjmuje się też różne definicje ścieżki: omówimy to bliżej w rozdziale o grafach.

Wprowadźmy dodatkowe nazewnictwo dotyczące drzew:

Gałąź to każda maksymalna ścieżka w drzewie. Każda gałąź zaczyna się w korzeniu i kończy w liściu.
Wysokość drzewa to maksymalna długość gałęzi.
Dla $x \in V$, zbiór $V_x = \{y \in V : y \text{ jest potomkiem } x\}$ z relacją $S$ obciętą do $V_x$ nazywamy poddrzewem $V$.

Przykładowe poddrzewo $V_x$, gdzie $x$ to prawe dziecko korzenia:

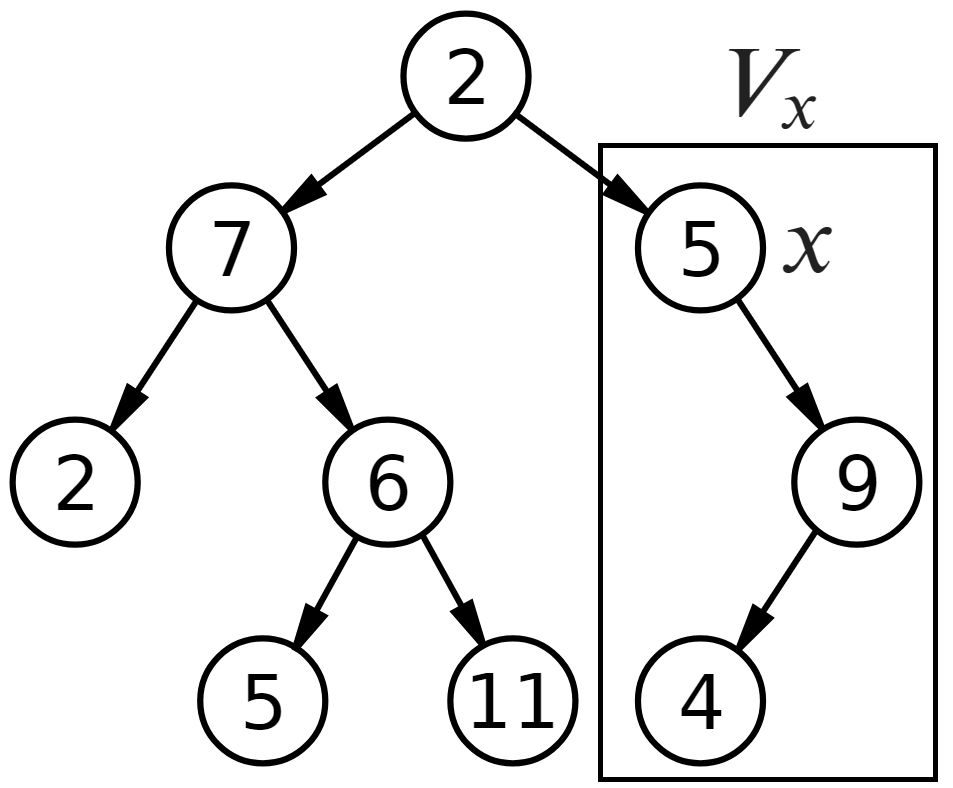
Fakt 1. Niech $V$ będzie drzewem o korzeniu $r$. Wtedy:

$V_x$ jest drzewem o korzeniu $x$.

Drzewo $V$ jest swoim własnym poddrzewem ($V$ = $V_r$).

Poddrzewo poddrzewa $V$ jest poddrzewem $V$.

Jeśli $W$ jest poddrzewem $W'$ i $W'$ jest poddrzewem $W$, to $W = W'$.

Z Faktu wynika, że relacja bycia poddrzewem jest zwrotna (2.), tranzytywna (3.) i słabo antysymetryczna (4.), czyli jest porządkiem częściowym. Elementem największym tego porządku jest całe drzewo (1.).

Drzewem binarnym nazywamy takie drzewo, w którym każdy węzeł ma co najwyżej dwa dziecka, i spośród nich co najwyżej jedno jest lewym dzieckiem i co najwyżej jedno jest prawym dzieckiem.

Bardziej formalnie, na drzewie $V$ istnieją dodatkowe relacje $L$i $R$ (dla lewego i prawego dziecka odpowiednio) takie, że że dla wszystkich $x, y \in V$, $$x S y \iff x L y ~ \overline{\vee} ~ x R y,$$ (gdzie $\overline{\vee}$ oznacza alternatywę wykluczającą), oraz dla każdego $x$ istnieje co najwyżej jeden $y$ taki, że $x L y$ oraz co najwyżej jeden $y'$ taki, że $x R y'$. Oznacza to, że dziecko każdego węzła jest albo jego lewym dzieckiem, albo jego prawym dzieckiem. Zwracamy tu uwagę, że w zwykłym (niebinarnym) drzewie nie rozróżniamy kolejności wśród dziecek węzła.

Przykładem drzewa binarnego jest drzewo z początku rozdziału. W drzewie binarnym, rysując lewe lub prawe dziecko węzła, umieszczamy je z odpowiedniej strony pod tym węzłem. Zwracamy uwagę, że węzeł może mieć prawe dziecko, lecz nie mieć lewego dziecka (takim węzłem na drzewie z początku rozdziału jest węzeł z liczbą 5).

Z uwagi na rozróżnienie lewego i prawego dziecka danego węzła, można jednoznacznie określić pojęcia jego lewego oraz prawego poddrzewa:

Jeśli $y$ jest lewym [prawym] dzieckiem węzła $x$, to poddrzewo $V_y$ nazywamy lewym [prawym] poddrzewem $x$.

To pozwala nam na inny opis drzew binarnych. Drzewo takie można rekurencyjnie opisać jako następującą trójkę obiektów:

Węzeł, który jest korzeniem,
Lewe poddrzewo korzenia (jeśli istnieje),
Prawe poddrzewo korzenia (jeśli istnieje).

Z takiego opisu drzewa będzie korzystać implementacja drzew binarnych: klasa BinaryTree. Wewnętrznie, instancje tej klasy będą używały trzech artybutów:

key - obiekt przechowany w korzeniu drzewa.
left - instancja BinaryTree reprezentująca lewe poddrzewo, lub None, jeśli lewe poddrzewo nie istnieje.
right - instancja BinaryTree reprezentująca prawe poddrzewo, lub None, jeśli prawe poddrzewo nie istnieje.

O klasie BinaryTree można również myśleć jako o pojedynczym węźle drzewa binarnego: wtedy key jest obiektem przechowywanym w tym węźle, left jego lewym dzieckiem (lub None), a right jest prawym dzieckiem (lub None).

Początkową wartość key określimy w konstruktorze drzewa. Wyposażymy też klasę BinaryTree w metody insert_left(key) oraz insert_right(key) (głównie w celach demonstracyjnych), które tworzą nowy węzeł przechowujący klucz key i ustawiają węzeł jako lewe (odpowiednio prawe) dziecko korzenia. Dla każdej z funkcji musimy rozważyć dwa przypadki: jeśli korzeń nie ma jeszcze odpowiedniego dziecka, lub już je ma. Dla insert_left(key), przypadki wyglądają następująco (dla insert_right(key) sa one analogiczne):

Jeśli korzeń nie ma lewego poddrzewa, to tworzymy nowy węzeł t z wartością key i ustawiamy t jako lewe dziecko korzenia.
Jeśli korzeń ma prawe poddrzewo, to tworzymy nowy węzeł t z wartością key, ustawiamy lewe poddrzewo korzenia jako lewe poddrzewo t, następnie ustawiamy t jako lewe dziecko korzenia.

Poniżej pokazujemy implementację klasy BinaryTree uzupełnioną o dodatkowe metody służące do odczytywania atrybutów key, left, right oraz ustawienia nowego key.

In [1]:

class BinaryTree:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None

    def insert_left(self, key):
        t = BinaryTree(key)
        if self.left is None:
            self.left = t
        else:
            t.left = self.left
            self.left = t

    def insert_right(self, key):
        t = BinaryTree(key)
        if self.right is None:
            self.right = t
        else:
            t.right = self.right
            self.right = t
            
    def get_left_child(self):
        return self.left

    def get_right_child(self):
        return self.right

    def set_root_val(self, obj):
        self.key = obj

    def get_root_val(self):
        return self.key

    def __str__(self):
        return f"[{self.key}; {self.left}; {self.right}]"

Powyższa implementacja zawiera jeszcze jedną metodę: __str__(). Napisowa reprezentacja drzewa przedstawia klucz jego korzenia oraz rekurencyjnie wyznaczone napisowe reprezentacje jego poddrzew (jeśli istnieją). W pliku binary_tree.py znajduje się jeszcze kompletniejsza implementacja, uzupełniona o funkcje pozwalające na trawersowanie drzewa. O trawersowaniu drzewa będzie traktować dalszy rozdział.

Poniżej przykładowe użycie drzewa:

Drzewa wyrażeń arytmetycznych ¶

Drzewa wyrażeń arytmetycznych to drzewa binarne reprezentujące wyrażenie arytmetyczne. Drzewo takie ma jedną z dwóch postaci:

Liczba (lub symbol oznaczający liczbę) jest przechowywana jako drzewo składające się tylko z korzenia, który przechowuje tę liczbę (stałą).
Działanie arytmetyczne postaci $L \circ R$, gdzie $L$ i $R$ są wyrażeniami, a $\circ$ działaniem, jest przechowywane jako drzewo, w którego korzeniu znajduje się $\circ$, a którego lewe i prawe poddrzewo reprezentują $L$ i $R$ odpowiednio.

Przykładowo, poniższe drzewo reprezentuje wyrażenie $(a + b) \cdot c + 7$:

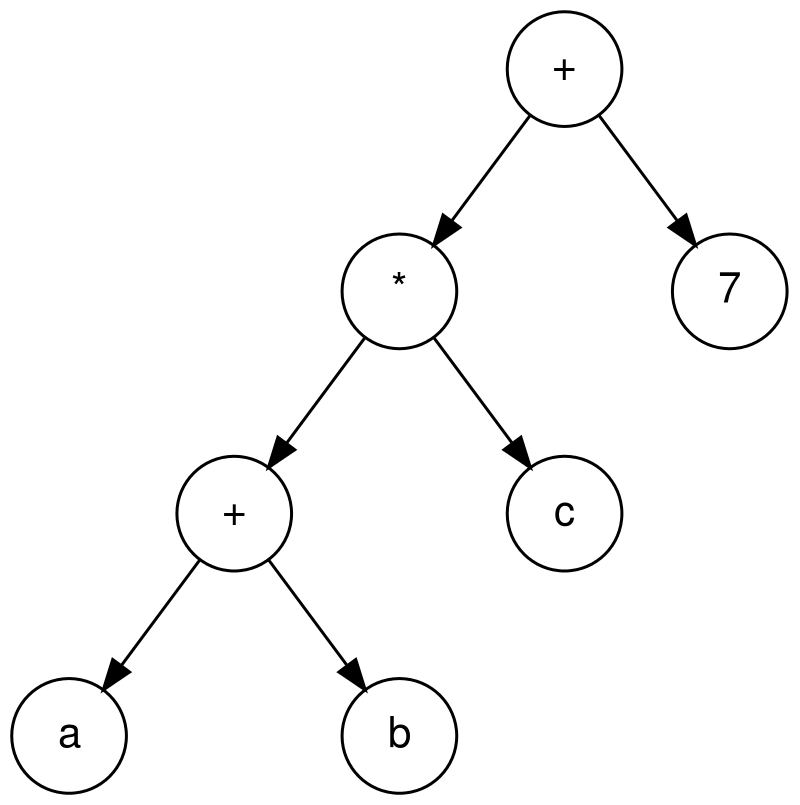
Źródło obrazu: Wikipedia.org, na licencji Creative Commons

Obserwujemy następujące własności drzewa wyrażenia:

Węzłami wewnętrznymi są dokładnie te węzły, które zawierają działania. Każdy taki węzeł ma oba dziecka.
Równoważnie, liśćmi drzewa są dokładnie te węzły, które zawierają liczby (bądź symbole).

Naszym celem będzie napisanie dwóch algorytmów:

Dla wyrażenia arytmetycznego, utworzenie drzewa tego wyrażenia (parsowanie).
Dla drzewa wyrażenia arytmetycznego, zawierającego w liściach liczby, wyliczenie wartości reprezentowanego wyrażenia (ewaluacja).

Parsowanie wyrażeń ¶

Uściślijmy, jakie wyrażenia będziemy konwertować do postaci drzewa wyrażeń. Będą to w pełni znawiasowane wyrażenia w notacji zwykłej (infiksowej). Oznacza to, że nawiasy kładziemy wokół każdego pełnego działania arytmetycznego, lecz nie wokół liczb i symboli. Przykładami w pełni znawiasowanych wyrażeń są:

( ( 10 + 5 ) * 3 )
( 1 + ( 2 + ( 3 + 4 ) ) )
100

Wejściem dla algorytmu będzie ciąg tokenów. Istnieją cztery rodzaje tokenów: lewy nawias, prawy nawias, operator i argument (liczba lub symbol).

Lewy operator otwiera pełne wyrażenie arytmetyczne: dla tego wyrażenia konstruujemy drzewo, którego węzeł przechowuje działanie, a poddrzewa jego podwyrażenia.
Prawy nawias kończy pełne wyrażenie.
Argument musi zostać wczytany do odpowiedniego liścia.
Operator musi zostać wczytany do węzła wewnętrznego.

Podobnie jak przy konwersji wyrażeń do ONP (wykład 3), wymagamy obecności białych znaków między tokenami.

Kroki algorytmu parsowania drzewa. W każdym kroku pamiętamy węzeł, w którym działamy.

Stwórz nowe drzewo t. Aktualnym węzłem jest korzeń.

Dla kolejnych tokenów z wejścia:
2a. Jeśli token to '(': stwórz nowe, lewe dziecko aktualnego węzła i zstąp do niego.
2b. Jeśli token jest operatorem: ustaw wartość rodzica aktualnego węzła na wartość tokenu. Stwórz nowe, prawe dziecko rodzica węzła i przejdź doń.
2c. Jeśli token jest argumentem, ustaw wartość aktualnego węzła na wartość tokenu.
2d. Jeśli token to ')': wróć do rodzica aktualnego węzła.

Zwróć drzewo t.

W algorytmie, rodzice węzłów pamiętamy, odkładając je na stos za każdym zstąpieniem w poddrzewo. W ten sposób zawartość stosu wraz z aktualnym węzłem stanowi ścieżkę z korzenia do aktualnego węzła.

Przykład: ( 1 + ( 2 * 3 ) ). Kolejne kroki algorytmu wyglądają następująco (czerwona kropka notuje aktualny węzeł drzewa):

Wczytany token	Krok	Zbudowane drzewo po wykonaniu kroku
(początek algorytmu)	1. Stwórz nowe drzewo, aktualnym węzłem jest korzeń.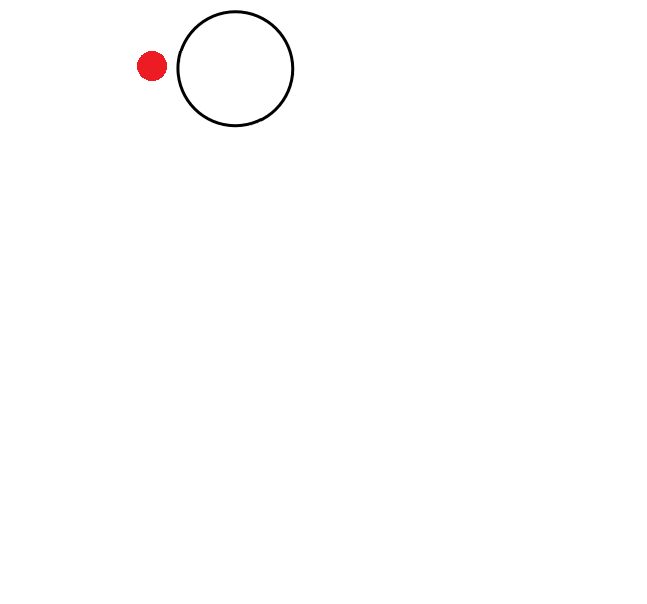
`(`	2a. Stwórz nowe, lewe dziecko aktualnego węzła i zstąp do niego.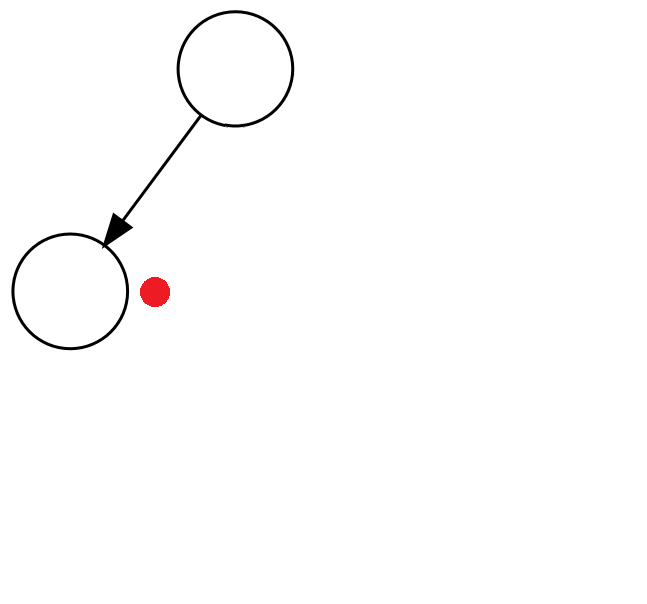
`1`	2c. Ustaw wartość aktualnego węzła na wartość tokenu.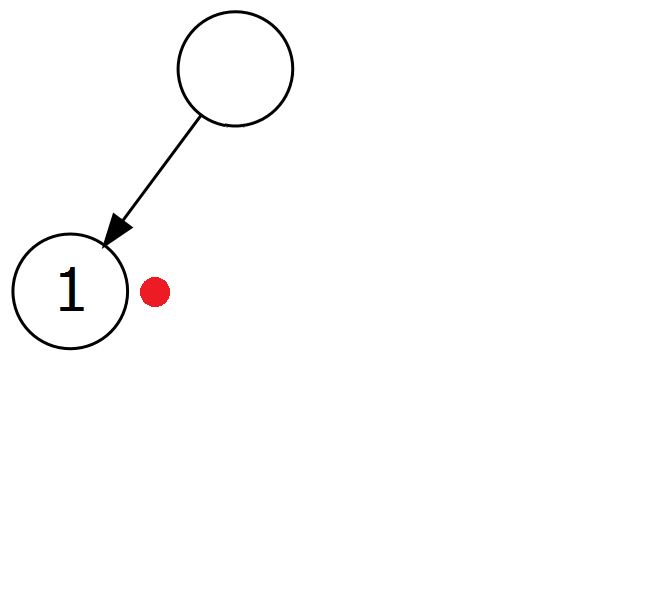
`+`	2b. Ustaw wartość rodzica aktualnego węzła na wartość tokenu. Stwórz nowe, prawe dziecko rodzica węzła i przejdź doń.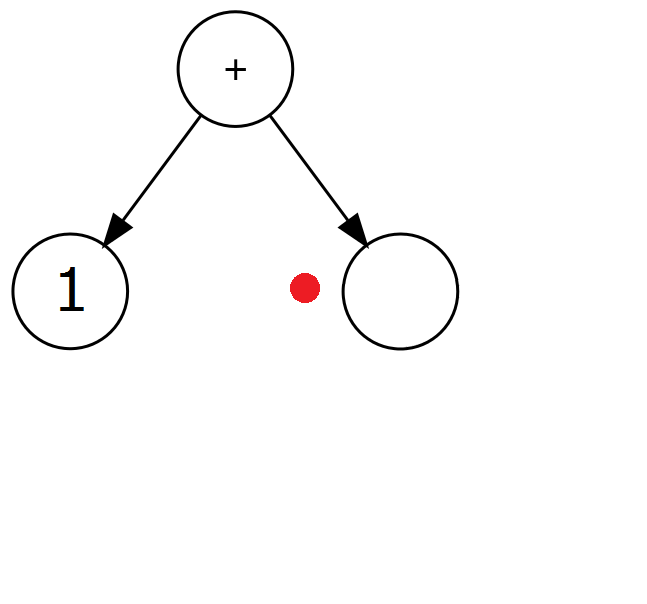
`(`	2a. Stwórz nowe, lewe dziecko aktualnego węzła i zstąp do niego.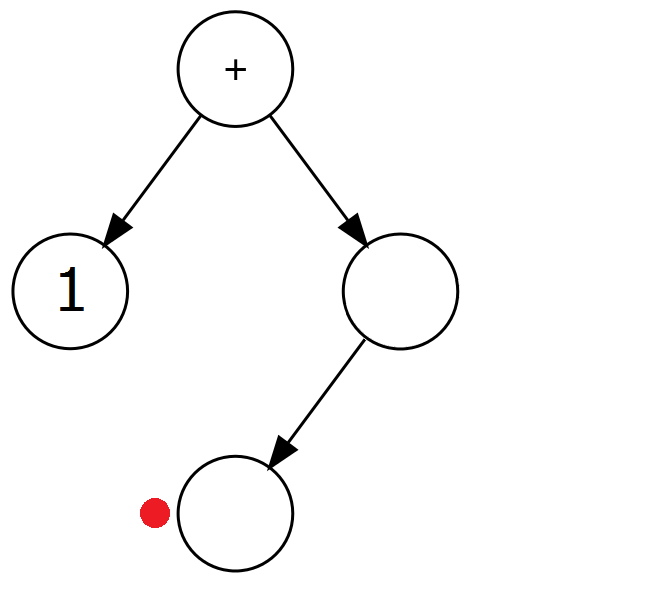
`2`	2c. Ustaw wartość aktualnego węzła na wartość tokenu.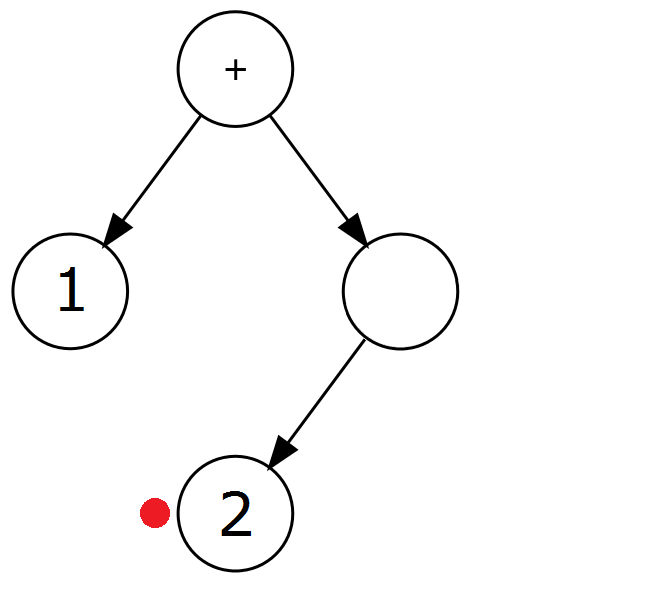
`*`	2b. Ustaw wartość rodzica aktualnego węzła na wartość tokenu. Stwórz nowe, prawe dziecko rodzica węzła i przejdź doń.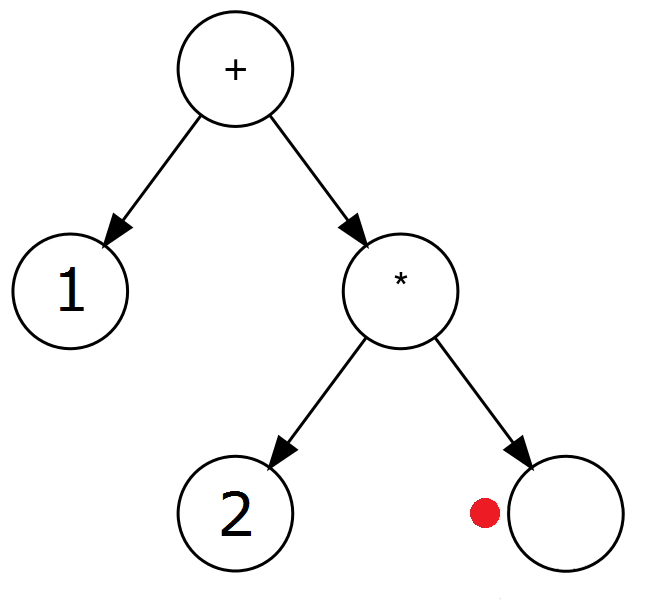
`3`	2c. Ustaw wartość aktualnego węzła na wartość tokenu.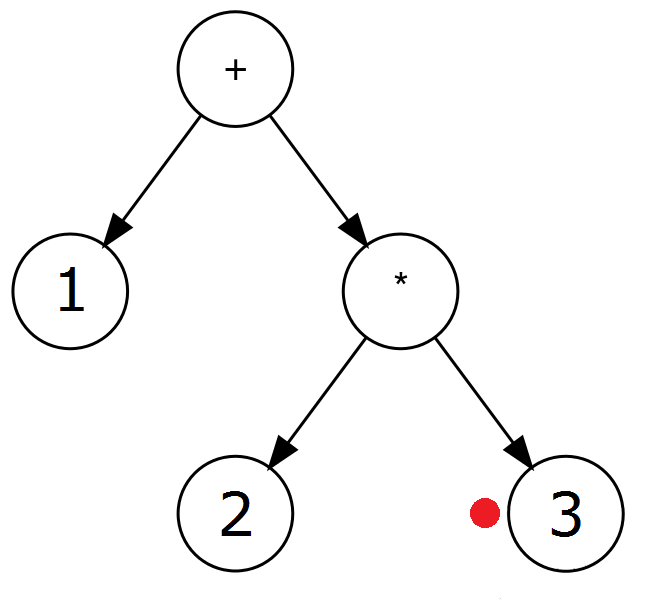
`)`	2d. Wróć do rodzica aktualnego węzła.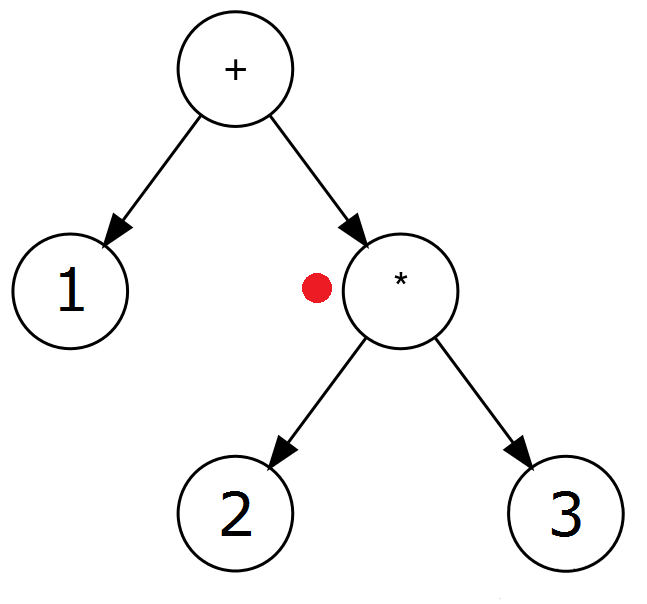
`)`	2d. Wróć do rodzica aktualnego węzła.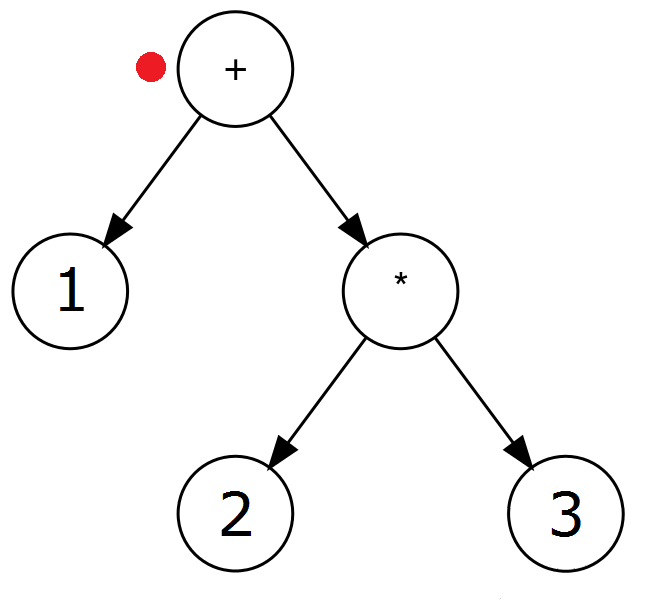

Ewaluacja wyrażenia w drzewie i implementacja parsera ¶

Ewaluacja drzewa reprezentującego wyrażenie jest prosta:

Jeśli drzewo nie ma lewego ani prawego dziecka (czyli reprezentuje liczbę), zwracamy wartość przechowywaną w korzeniu.
W przeciwnym wypadku drzewo reprezentuje działanie przechowywane w korzeniu, a lewe i prawe poddrzewo reprezentują podwyrażenia po obu stronach działania. Wtedy rekurencyjnie wyliczamy wartości tych poddrzew, a na uzyskanych wartościach wykonujemy działanie z korzenia.

Zaimplementujemy klasę Parser (parsowanie - odczytywanie struktury podanego wejścia), której zadaniem jest zbudowanie drzewa podanego w konstruktorze wyrażenia. Klasa będzie posiadać metody do wyliczenia wartości tego wyrażenia i przedstawienia go z powrotem w postaci napisu.

Obiekt klasy Parser będzie miał następujące atrybuty:

tokens - lista tokenów rozważanego wyrażenia.
ast - obiekt klasy BinaryTree: drzewo wyrażenia, które parser zbuduje.
opers - atrybut klasy (nie instancji). Słownik stowarzyszający tokeny wyrażeń arytmetycznych z funkcjami, które je wykonują.

Klasa ma też metody:

__init__(self, infix_expr) - tworzy instancję Parser, która parsuje podane w pełni znawiasowane wyrażenie w notacji infiksowej.
make_ast(self) - metoda do użytku wewnętrznego, konstruuje drzewo ast z listy tokenów tokens.
eval(self) - zwraca wartość drzewa wyrażenia (czyli wartość sparsowanego wyrażenia).
print_exp(self) - zwraca napis, odpowiadający drzewu wyrażeń (wartość oryginalnego wyrażenia).

Pełna implementacja Parser znajduje się w pliku parse_tree.py. Nie omówimy tutaj jej całej - zauważymy, że make_ast() to implementacja algorytmu opisanego w poprzednim podrozdziale, a eval() to podany wyżej algorytm ewaluacji. Zwrócimy jednak uwagę na pewne szczegóły implementacji.

operator to standardowy moduł Pythona, który zawiera funkcje odpowiadające operatorom arytmetycznym. Przykładowo, funkcja operator.add to funkcja dwóch argumentów, zwracająca ich sumę.
Słownik opers stowarzysza tokeny oznaczające działania arytmetyczne z odpowiednimi funkcjami z modułu operator. Jego definicja wygląda następująco (jest on atrybutem klasy Parser):
```
opers = {'*': operator.mul, '/': operator.truediv,
           '+': operator.add, '-': operator.sub}
```
wobec czego można go użyć w np. następujący sposób:
```
Parser.opers['+'](2, 3) # == 2 + 3
```
W taki sposób opers jest używany w metodzie eval():
```
return Parser.opers[tree.get_root_val()](res1, res2)
```
gdzie tree.get_root_val() jest operatorem z korzenia drzewa tree, zaś res1 i res2 to wartości lewego i prawego poddrzewa tree odpowiednio.

Trawersowanie drzew ¶

Trawersowanie drzewa to proces polegający na odwiedzeniu jego węzłów w pewnej ustalonej kolejności. Odwiedzenie węzła polega na wykonaniu operacji na obiekcie, który ten węzeł przechowuje (na przykład obiekt można wypisać).

Dla drzew binarnych, wyróżniamy trzy sposoby trawersowania. Każdy ze sposobów polega na odwiedzeniu korzenia drzewa, oraz rekurencyjnym trawersowaniu jego lewego i prawego poddrzewa (jeśli istnieją). Są to sposoby preorder, inorder oraz postorder.

Trawersując drzewo w kolejności preorder, odwiedzamy najpierw korzeń, a potem jego lewe i prawe poddrzewo korzenia w kolejności preorder.
Trawersując drzewo w kolejności inorder, odwiedzamy najpierw jego lewe poddrzewo w kolejności inorder, następnie korzeń, a potem prawo poddrzewo korzenia w kolejności inorder.
Trawersując drzewo w kolejności postorder, odwiedzamy najpierw lewe i prawe poddrzewo korzenia w kolejności postorder, a potem korzeń.

Ściślej, opiszemy kroki trzech algorytmów:

Kroki preorder (wejście: drzewo/węzeł T):

Odwiedź węzeł T.

Odwiedź lewe poddrzewo T algorytmem preorder. 3.Odwiedź prawe poddrzewo T algorytmem preorder.

Kroki inorder (wejście: drzewo/węzeł T):

Odwiedź lewe poddrzewo T algorytmem inorder.

Odwiedź węzeł T. 3.Odwiedź prawe poddrzewo T algorytmem inorder.

Kroki postorder (wejście: drzewo/węzeł T):

Odwiedź lewe poddrzewo T algorytmem postorder.

Odwiedź prawe poddrzewo T algorytmem postorder.

Odwiedź węzeł T.

Dla drzewa wyrażenia ( 1 + ( 2 * 3 ) ), które skonstruowaliśmy w poprzednim rozdziale, algorytmy trawersują węzły w następującej kolejności:

preorder: + 1 * 2 3
inorder: 1 + 2 * 3
postorder: 1 2 3 * +

Można zwrócić uwagę, że kolejne tokeny uzyskane przy trawersowaniu preoder układają się w wyrażenie NP równoważne oryginalnemu wyrażeniu. Podobnie, tokeny kolejno uzyskane przy trawersowaniu postorder układają się w odpowiednie wyrażenie ONP. Natomiast te uzyskane algorytmem inorder to oryginalne wyrażenie infiksowe, jednak pozbawione nawiasów. Fakty te uogólniają się na wszystkie drzewa wyrażeń.

Algorytmy preoder, inorder i postorder zostały zaimplementowane w klasie BinaryTree jako metody. Odwiedzanie węzła polega na wypisaniu wartości, którą przechowuje.

Drzewa wyszukiwań binarnych ¶

Drzewo wyszukiwań binarnych to szczególny rodzaj drzewa binarnego, w którego węzłach przechowujemy parami porównywalne elementy (według pewnego praporządku).

Definicja. Drzewo binarne $(V, S)$ jest drzewem wyszukiwań binarnych wtedy, gdy dla każdego węzła $x \in V$, obiekt przechowywany w $x$ jest nie mniejszy od obiektów przechowywanych w węzłach lewego poddrzewa $x$, i nie większy od obiektów przechowywanych w węzłach prawego poddrzewa $x$.

Rysunek poniżej przedstawia przykład drzewa wyszukiwań binarnych, którego węzły przechowują liczby:

Źródło obrazu: Wikipedia.org, na licencji Creative Commons

Jak widzimy, korzeń drzewa przechowuje wartość 8, która jest nie mniejsza od wartości przechowywanym w lewym poddrzewie korzenia (te wartości to 1, 3, 4, 6 i 7), ale nie większa od wartości przechowywanych w prawym poddrzewie (10, 13 i 14). Podobnie dla węzła przechowującego 3, jego lewe poddrzewo przechowuje wartość 1, a prawe poddrzewo 4, 6 i 7.

W ogólności, wartości przechowywane w węzłach mogą się powtarzać.
Poddrzewo drzewa wyszukiwań binarnych jest drzewem wyszukiwań binarnych.

Przedstawimy teraz algorytm umieszczania w drzewie wyszukiwań binarnych nowego węzła o zadanych wartości, a następnie algorytm efektywnego sprawdzania, czy w drzewie znajduje się podana wartość. W obu algorytmach korzystamy z rekurencyjnego opisu drzew, w którym drzewo składa się z korzenia i swoich poddrzew.

Umieszczanie nowego elementu ¶

W najprostszym wariancie, nowy elementy dokładany jest jako nowy liść danego drzewa tak, aby drzewo pozostało binarnym drzewem poszukiwań. Możliwe jest, że elementy równe dokładanemu znajdują się już w drzewie.

Niech $T$ będzie drzewem, w którego korzeniu przechowywany jest obiekt $x$. Do drzewa chcemy dodać element $y$. Rozpatrzmy przypadki:

Jeśli $y$ jest mniejszy niż $x$, wówczas $y$ musi pojawić się jako węzeł w lewym poddrzewie korzenia. Mamy wtedy dwa podprzypadki:
- Korzeń nie ma lewego poddrzewa. Zatem $y$ musi zostać dodany jako nowy liść, który staje się lewym poddrzewem korzenia.
- Korzeń ma lewe poddrzewo (które jest drzewem wyszukiwań binarnych). Wówczas $y$ musi zostać dodane do tego poddrzewa.
Analogicznie, jeśli $y$ jest większy niż $x$, wówczas $y$ musi pojawić się jako węzeł w prawym poddrzewie korzenia. Mamy wtedy dwa podprzypadki:
- Korzeń nie ma prawego poddrzewa. Zatem $y$ musi zostać dodany jako nowy liść, który staje się prawym poddrzewem korzenia.
- Korzeń ma prawe poddrzewo (które jest drzewem wyszukiwań binarnych). Wówczas $y$ musi zostać dodane do tego poddrzewa.
Jeśli $y$ jest równy $x$, to może zostać umieszczony w dowolnym z poddrzew korzenia. Możemy zatem traktować ten przypadek identycznie z pierwszym.

Powyższy opis jest dobrym schematem rekurencyjnego postępowania: we wszystkich przypadkach następuje redukcja problemu: dołożenia nowego liścia, lub dołożenia elementu do mniejszego drzewa. Stąd rekurencyjny opis algorytmu:

Kroki algorytmu insert (T - drzewo/węzeł, key - nowy obiekt do wstawienia):

Jeśli key jest mniejszy lub równy obiektowi w T:
1a. Jeśli korzeń nie ma lewego poddrzewa, dodaj do korzenia nowe lewe dziecko z obiektem key.
1b. W przeciwnym wypadku, wykonaj insert dla lewego dziecka T i key.

Jeśli key jest większy od obiektu w T:
2a. Jeśli korzeń nie ma prawego poddrzewa, dodaj do korzenia nowe prawe dziecko z obiektem key.
2b. W przeciwnym wypadku, wykonaj insert dla prawego dziecka T i key.

Wyszukiwanie elementu ¶

Wyszukiwanie elementu realizujemy na podobnej zasadzie, co wstawianie elementu: poprzez redukcję problemu do poddrzew. Niech $T$ będzie drzewem, w którego korzeniu znajduje się obiekt $x$. Chcemy rozstrzygnąć, czy w $T$ znajduje się węzeł przechowujący obiekt $y$. Rozważmy przypadki:

Jeśli $y$ jest równe $x$, to odpowiedź brzmi TAK.
Jeśli $y$ jest mniejsze od $x$, to $T$ zawiera $y$ dokładnie wtedy, gdy ma lewe poddrzewo, i to poddrzewo zawiera $y$.
Jeśli $y$ jest większe od $x$, to $T$ zawiera $y$ dokładnie wtedy, gdy ma prawe poddrzewo, i to poddrzewo zawiera $y$.

Stąd naturalny algorytm:

Kroki algorytmu search (T - drzewo/węzeł, key - szukany obiekt):

Jeśli key jest równy obiektowi w T: zwróć TAK.

Jeśli key jest mniejszy od obiektu T:
2a. Jeśli korzeń nie ma lewego poddrzewa, zwróć NIE.
2b. W przeciwnym wypadku, wykonaj search dla lewego dziecka T i key i zwróć jego wynik.

Jeśli klucz jest większy od obiektu w T:
3a. Jeśli korzeń nie ma prawego poddrzewa, zwróć.
3b. W przeciwnym wypadku, wykonaj insert dla prawego dziecka T i key i zwróc jego wynik.

Kod drzew wyszukiwań binarnych znajduje się w pliku bst.py. Jego kluczowa część wygląda następująco:

class BinarySearchTree:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None

    def insert(self, key):
        if key <= self.key:
            if self.left:
                self.left.insert(key)
            else:
                self.left = BinarySearchTree(key)
        else:
            if self.right:
                self.right.insert(key)
            else:
                self.right = BinarySearchTree(key)

    def search(self, key):
        if self.key == key:
            return True
        if key < self.key:
            if not self.left:
                return False
            return self.left.search(key)
        if not self.right:
            return False
        return self.right.search(key)

Atrybuty key, left i right mają to samo znaczenie, co w zwykłych drzewach binarnych. Metody insert(key) i search(key) implementują algorytmy opisane w dwóch poprzednich podrozdziałach. Implementacja w pliku bst.py zawiera dodatkowe metody, między innymi służące do trawersowania drzewa.

Fakt 2. Trawersowanie drzewa w porządku inorder odwiedza obiekty w kolejności niemalejącej.

Powyższy Fakt ma konsekwencje dla pewnych algorytmów sortowań.

Rozważmy teraz zastosowanie drzew wyszukiwań binarnych jako zbioru (lub ściślej: multizbioru, czyli "zbioru", który może zawierać wiele takich samych elementów). W tym celu zastanówmy się nad czasem algorytmów insert i search. Zauważamy, że:

W treści obu algorytmów znajdują się jedynie operacje o stałym czasie, oraz jedno rekurencyjne wywołanie tego algorytmu.
Każde rekurencyjne wywołanie dowolnego z tych algorytmów wykonuje się na dziecku poprzedniego węzła. Zatem maksymalna głębokość rekurencji nie przekracza wysokości drzewa.

Wykład 6 - drzewa i drzewa binarne¶

Spis treści¶

Drzewa ¶

Drzewa binarne ¶