G. Jagiella

Skrypt do wykładu Programowanie 2 (Python)

ostatnia modyfikacja: 31.05.2020

Wykład 5 (cz. 2) - algorytmy sortujące II¶

Spis treści¶

"Dziel i zwyciężaj"
Merge sort - sortowanie przez scalanie
- Scalanie list
- Sortowanie
Quicksort - sortowanie szybkie
Algorytmy hybrydowe i podsumowanie

"Dziel i zwyciężaj"¶

"Dziel i zwyciężaj" ("dziel i rządź", "divide and conquer", "divide et impera") - technika w programowaniu polegająca na rekurencyjnym dzieleniu zadanego problemu na podproblemy (a podproblemy na jeszcze mniejsze podproblemy), aż staną się dostatecznie małe, by je z osobna rozwiązać w bezpośredni sposób.

Przykład (celowo trywialny): rekurencyjny algorytm wyznaczania liczb z ciągu Fibonacciego.

def fib(n):
    if n in (0, 1):
        return n
    return fib(n - 1) + fib(n - 2)

Problemem jest tu znalezienie $n$-tego wyrazu ciągu. Dzielimy go na podproblemy: znalezienie wyrazów $(n-1)$-ego i $(n-2)$-ego. Gdy je znajdziemy, wystarczy je dodać. To jest redukcja problemu: gdy już zredukujemy podproblemy do znalezienia wyrazów zerowego i pierwszego, po prostu je podajemy. W dobrym schemacie dziel i zwyciężaj, tak jak w każdym schemacie rekurencyjnym, ważne jest, aby nie popaść w nieskończony regres.

Na idei dziel i zwyciężaj opierają się dwa następne algorytmy, które omówimy.

Merge sort - sortowanie przez scalanie ¶

W tym podrozdziale omówimy sortowanie przez scalanie, zaczynając od zagadnienia scalania list.

Scalanie list ¶

Scalanie (merging) polega na połączeniu dwóch posortowanych list w jedną (też posortowaną) listę. Otrzymując listy l1 i l2 długości $n$ i $m$ odpowiednio, chcemy utworzyć posortowaną listę result długości $n + m$, złożoną z elementów list l1 i l2. Przykładowo:

l1 = [2, 3, 6, 10, 12]
l2 = [1, 4, 5, 7, 10, 16, 20]
result = merge(l1, l2)
# [1, 2, 3, 4, 5, 6, 7, 10, 10, 12, 16, 20]

Idea algorytmu merge: dokładamy do result niewykorzystane elementy z początków l1 i l2 tak długo, aż jedna z list stanie się pusta. Wtedy dokładamy pozostałe elementy z pozostałej listy do result. Wykorzystane elementy śledzimy, zapamiętując indeksy pierwszych elementów obu scalanych list, które nie zostały jeszcze wykorzystane (tzn. nie usuwamy elementów z początku l1 i l2 - to złe dla złożoności). Jeśli na listach l1 i l2 znajdują się równe elementy, to preferujemy te z l1 (ta decyzja będzie miała znaczenie dla stabilności jednego z algorytmów).

Przykład dla list powyżej: śledzimy niewykorzystane elementy przy pomocy indeksów i i j:

Krok 1:
l1 = [2, 3, 6, 10, 12]    l2 = [1, 4, 5, 7, 10, 16, 20]     result = []
      i                         j

lst[i] > lst[j] (2 > 1), zatem dokładamy lst[j] do result oraz zwiększamy j

Krok 2:
l1 = [2, 3, 6, 10, 12]    l2 = [1, 4, 5, 7, 10, 16, 20]     result = [1]
      i                            j

lst[i] <= lst[j] (2 <= 4), zatem dokładamy lst[i] do result oraz zwiększamy i

Krok 3:
l1 = [2, 3, 6, 10, 12]    l2 = [1, 4, 5, 7, 10, 16, 20]     result = [1, 2]
         i                         j

lst[i] <= lst[j] (3 <= 4), zatem dokładamy lst[i] do result oraz zwiększamy i
...

Kod merge pominiemy: znajduje się w materiałach w pliku merge_sort.py.

Sortowanie ¶

Idea algorytmu: dziel i zwyciężaj. Dzielimy listę na dwie połówki, które sortujemy rekurencyjnymi wywołaniami sortowania przez scalanie, a następnie te posortowane połówki scalamy. "Połówki" mogą różnić się rozmiarem o jeden element (w przypadku listy długości nieparzystej).

Redukcja problemu polega więc na zmniejszeniu rozmiaru listy, którą musimy posortować. Gdy lista jest dostatecznie mała (pusta lub jednoelementowa), jest już posortowana - podproblem jest rozwiązany.

Uwaga. Przedstawiony tutaj algorytm, zamiast sortować podaną listę, tworzy nową listę odpowiadającą posortowanej liście podanej na wejściu algorytmu. Możliwa jest jego modyfikacja, która nie tworzy tej listy (tzn. sortowanie przebiega w w miejscu, in-place).

Znów w postaci algorytmicznej:

Kroki algorytmu merge_sort (lst: lista):

Jeśli lista ma mniej niż dwa elementy, zwracamy ją.

Dzielimy lst na dwie połówki: left i right.

Każdą połówkę sortujemy rekurencyjnie algorytmem merge_sort.

Posortowane połówki scalamy i zwracamy.

Schemat działania merge_sort ilustruje poniższy rysunek. Czerwone strzałki oznaczają podziały list na połówki (kroki 2. kolejnych wywołań rekurencyjnych), zielone scalanie (kroki 4. wywołań). Lista dzielona jest rekurencyjnie na coraz mniejsze listy, aż do jednoelementowych, które są następnie scalane do list, z których zostały wydzielone.

Źródło obrazu: Wikipedia.org, na licencji Creative Commons

Stwierdzenie. Algorytm merge_sort poprawnie sortuje listy i robi to w sposób stabilny.
Dowód. Skorzystamy z zasady indukcji pod postacią zasady minimum. Załóżmy, że dla pewnej listy lst, merge_sort nie sortuje lst, lub sortuje ją w sposób niestabilny. Bez straty ogólności można założyć, że lst jest najkrótszą taką listą. lst nie może być długości $0$ lub $1$, gdyż takie listy są już posortowane i merge_sort po prostu je zwraca. Zatem merge_sort dzieli lst na połówki left i right, a każda z nich jest krótsza, niż lst. Na tych połówkach wywoływane są rekurencyjnie merge_sort. Niech left1 = merge_sort(left) i right1 = merge_sort(right). left1 i right1 są posortowanymi left i right, zatem ich można je scalić w posortowaną listę. To dowodzi, że merge_sort poprawnie sortuje lst.
Żeby pokazać, że posortowanie lst jest stabilne, wybierzmy dwa równe w sensie praporządku elementy a i b z nieposortowanej lst takie, że a występuje przed b. Mamy trzy przypadki:

a i b trafiły do połówki left. Wtedy występują na left1 w tej samej kolejności (bo left1 jest posortowane stabilnie), i po scaleniu left1 z right1 również wystąpią w tej kolejności.

a i b trafiły do połówki right. Przypadek jest analogiczny do 1.

a trafiło do left, b trafiło do right. Wtedy przy scalaniu left i right, a zostanie umieszczony w scaleniu przed b, ponieważ scalanie preferuje pobieranie elementów z pierwszej z list. $\dashv$

Fakt. Algorytm merge_sort działa w czasie $\Theta(n \log n)$.
Szczegółowy dowód wykracza poza zakres tego skryptu.

Kod merge_sort z wykładu, z pominięciem funkcji merge:

def merge_sort(lst):
    if len(lst) < 2:
        return lst

    n = len(lst) // 2
    left = lst[:n]
    right = lst[n:]
    return merge(merge_sort(left), merge_sort(right))

Podsumujemy cechy algorytmu sortowania przez scalanie:

Złożoność czasowa: zgodnie z Faktem, $\Theta(n \log n)$, bez rozróżnienia przypadków.
Złożoność pamięciowa: $\Theta(n)$ (to wymaga uzasadnień; łatwo jednak uzasadnić $\Omega(n)$, bo merge_sort tworzy nową listę, zamiast sortować podaną).
Stabilność: TAK, zgodnie ze stwierdzeniem.

Quicksort - sortowanie szybkie ¶

Ostatnim z omówionych algorytmów jest algorytm tzw. sortowania szybkiego.

Idea: podzielić listę na części: jedną złożoną z elementów "małych", jedną z "dużych". Następnie posortować je osobno rekurencyjnie i połączyć (nie scalić).

Wersja uproszczona i naiwna ¶

Poniżej pokażemy kroki uproszczonej wersji algorytmu sortowania szybkiego. Nie jest to wersja dobra dla wydajnej implementacji i ma charakter ilustracyjny. Wersja ta tworzy nową listę, odpowiadającą posortowanemu wejściu, nie sortuje podanej

Kroki algorytmu quick_sort_easy (gdzie lst to lista):

Jeśli lista ma mniej niż dwa elementy, zwracamy ją.

Wybieramy element z listy (tzw pivot).

Tworzymy trzy listy:
left - złożoną z elementów lst mniejszych od pivota.
middle - złożoną z elementów lst równych pivotowi w sensie praporządku.
right - złożoną z elementów lst większych od pivota.

Zwracamy:
quick_sort_easy(left) + middle + quick_sort_easy(right)

Ponieważ listy left i right są krótsze niż lst, problem redukuje się do ich posortowania, co uzyskujemy rekurencyjnymi wywołaniami quick_sort_easy. Redukcja zatrzymuje się na listach rozmiaru $0$ i $1$.

Powyższy uproszczony algorytm daje się łatwo zakodować (bardzo niewydajna implementacja):

# Wersja konstruujaca nowe listy:
def quick_sort_easy(lst):
    if len(lst) < 2:
        return lst

    pivot = lst[-1]
    left = [x for x in lst if x < pivot]
    middle = [x for x in lst if x == pivot]
    right = [x for x in lst if x > pivot]

    return quick_sort_easy(left) + middle + quick_sort_easy(right)

Problemem tej wersji algorytmu jest (niepotrzebne) tworzenie nowych list. Poniżej omówimy, jak obejść ten problem przez takie przearanżowanie elementów na liście, aby można z niej było wyodrębnić fragmenty, odpowiadające listom left i right.

Partycjonowanie ¶

Niech lst będzie listą. Jej fragmentem (lub segmentem) będziemy nazywać wszystkie elementy lst pomiędzy zadanymi indeksami i i j włącznie. Cała lista lst jest swoim własnym fragmentem dla indeksów 0 i len(lst) - 1.

Przez "fragment lo, hi" będziemy rozumieć fragment ustalonej listy ograniczony indeksami lo i hi (jak "low" i "high").

Definicja. Partycjonowaniem listy długości n nazywamy taką zmianę kolejności elementów na niej, żeby dla pewnego indeksu 0 $\leq$ i $\leq$ n-1 zachodził następujący warunek: każdy element z fragmentu 0, i-1 jest mniejszy lub równy od każdego elementu z fragmentu i, n-1.
Podobnie definiujemy partycjonowanie fragmentu listy.

Partycjonowanie listy (lub fragmentu) rozdziela jej elementy na "małe" i "duże". Przykładem jest poniższa ilustracja: oryginalna lista (pierwsza) i lista po spartycjonowaniu (druga). Na drugiej liście, wszystkie elementy pod indeksami mniejszymi od 11 są mniejsze od tych, które są pod indeksami 11 i większymi.

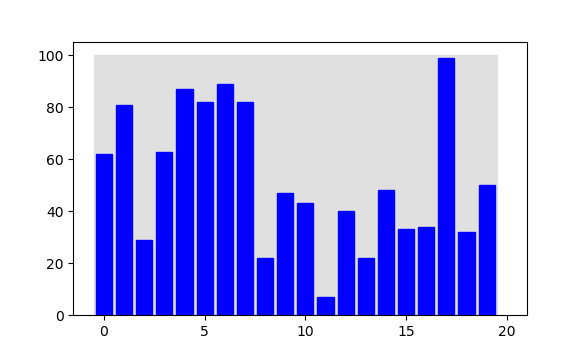
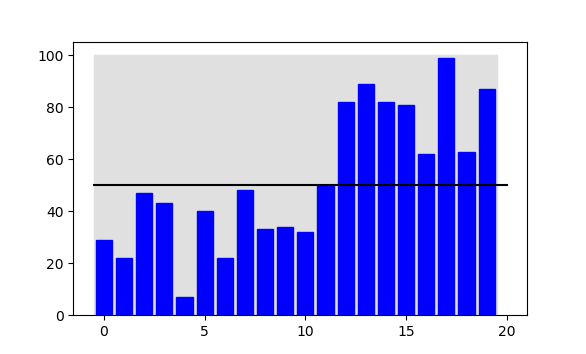
Partycjonowanie fragmentu lo, hi wykonujemy przez wybranie spośród jego elementu pivota, oraz umieszczenie pivota na końcu fragmentu (zamieniając go miejscami z elementem, który już tam stał). Dla uproszczenia założymy, że to ostatni element fragmentu został wybrany jako pivot. Następnie dla kolejnych indeksów j $=$ lo, lo+1,, $\ldots$, hi-1 badamy element pod indeksem j. Jeśli element jest większy lub równy pivotowi, kontynuujemy proces. Jeśli jednak w procesie napotkamy elementy, które są mniejsze od pivota, to przenosimy je na początkowy kawałek fragmentu: pierwszy taki napotkany element przenosimy pod indeks lo, następny pod lo+1, potem lo+2 itd. Przenoszenie elementu na inny indeks polega na zamienieniu go miejscami z elementem, pod który pod tym indeksem stoi. Kolejne indeksy, pod które przenosimy napotkane elementy śledzimy z użyciem pomocniczej zmiennej i (jej początkowa wartość to lo, zwiększamy ją za każdym razem, gdy dokonujemy zamiany).

Gdy już skończymy badanie kolejnych elementów, wykonujemy jeszcze jeden krok: zamieniamy miejscami pivot (element z końca fragmentu) z elementem pod indeksem i. Algorytm, oprócz zmiany kolejności elementów na podanym fragmencie, zwraca indeks i - nową pozycję pivota - jako wynik.

Kroki algorytmu partition (lst - lista, lo, hi - końce partycjonowanego fragmentu)

Niech i $=$ lo, pivot $=$ lst[hi].

Dla j = lo, lo+1, $\ldots$, hi:
Jeśli lst[j] < pivot:, zamień lst[i] z lst[j], zwiększ i o 1.

Zamień lst[i] z lst[hi].

Zwróć i.

Niezmiennik pętli PRE(i): elementy z fragmentu lo, i - 1 są mniejsze od pivot, elementy z fragmentu i, j - 1 nie; i $\leq$ j.

Kod algorytmu partition pomijamy - jest w materiałach z wykładu, plik quick_sort.py.

Quicksort (wersja właściwa)¶

Idea "poprawnego" algorytmu quicksort jest taka, jak dla wersji uproszczonej, ale gdzie zamiast nowo utworzonych list pracujemy na fragmentach, które partycjonujemy, a następnie rekurencyjnie sortujemy ich podfragmenty.

Podamy teraz kroki algorytmu quicksort sortującego zadany fragment listy. Aby posortować całą listę, wystarczy posortować fragment od początku do końca listy (czyli po prostu listę).

Kroki algorytmu quick_sort (lst: lista, lo, hi - fragment do posortowania):

Jeśli lo $\geq$ hi (fragment jest pusty), koniec.

Partycjonujemy fragment lo, hi otrzymując i (indeks pivota).

Sortujemy fragmenty lo, i - 1 oraz i + 1, hi algorytmem quick_sort.

Po spartycjonowaniu fragmentu lo, hi, jego (pod)fragment lo, i - 1 spełnia rolę listy left z wersji naiwnej. Podobnie, podfragment i + 1, hi spełnia rolę listy right. Pojedynczy element pod indeksem i - pivot partycjonowania - spełnia rolę middle.

Kod algorytmu (algorytm powyżej jest w nim implementowany przez funkcję quick_sort_segment, wewnętrzną dla quick_sort; sam quick_sort wywołuje quick_sort_segment na całej liście):

def quick_sort(lst):
    def quick_sort_segment(lst, lo, hi):
        if lo >= hi:
            return

        i = partition(lst, lo, hi)
        quick_sort_segment(lst, lo, i - 1)
        quick_sort_segment(lst, i + 1, hi)

    quick_sort_segment(lst, 0, len(lst) - 1)

Poniżej natomiast ilustracja działania. Na szaro zaznaczony jest aktualnie partycjonowany fragment:

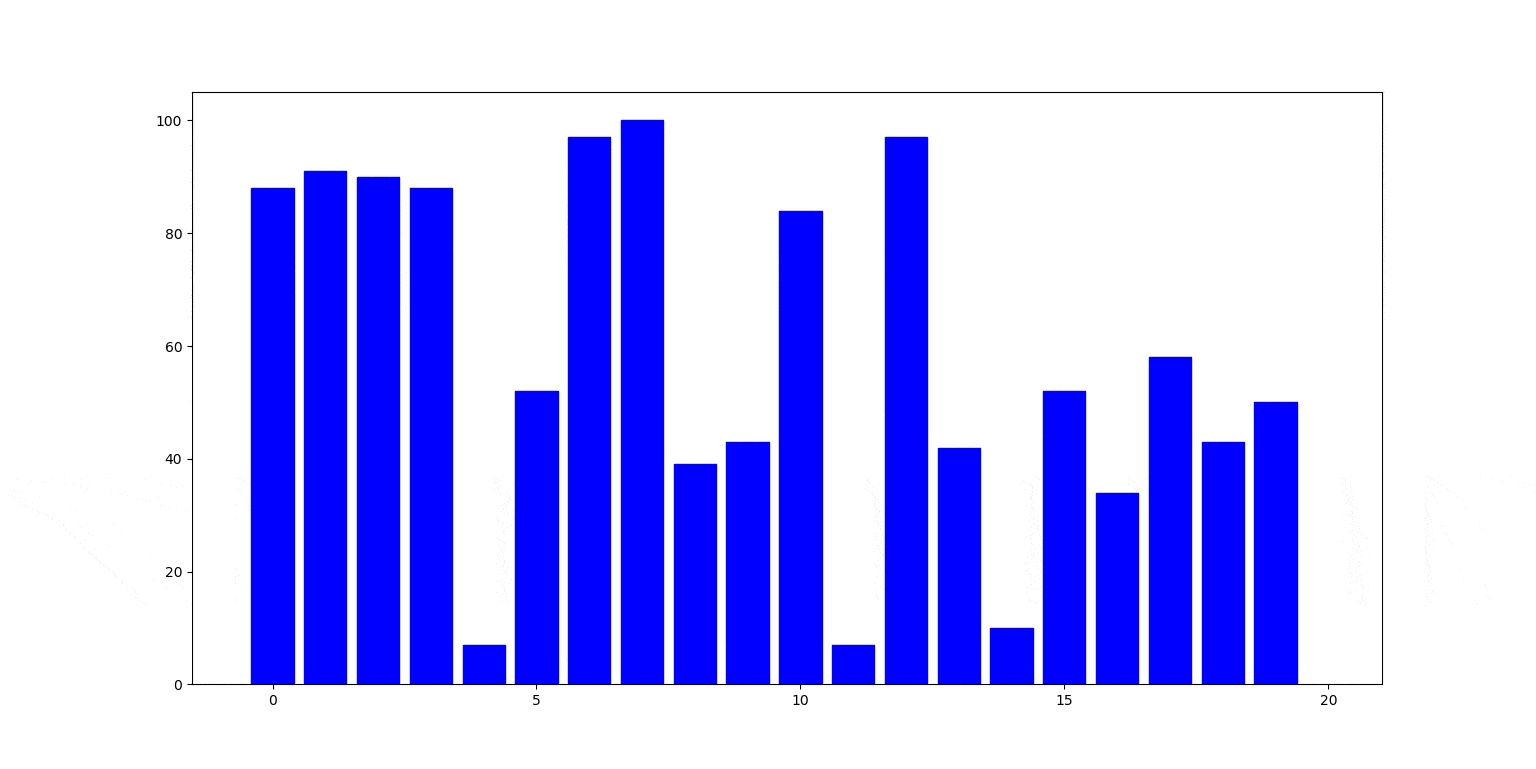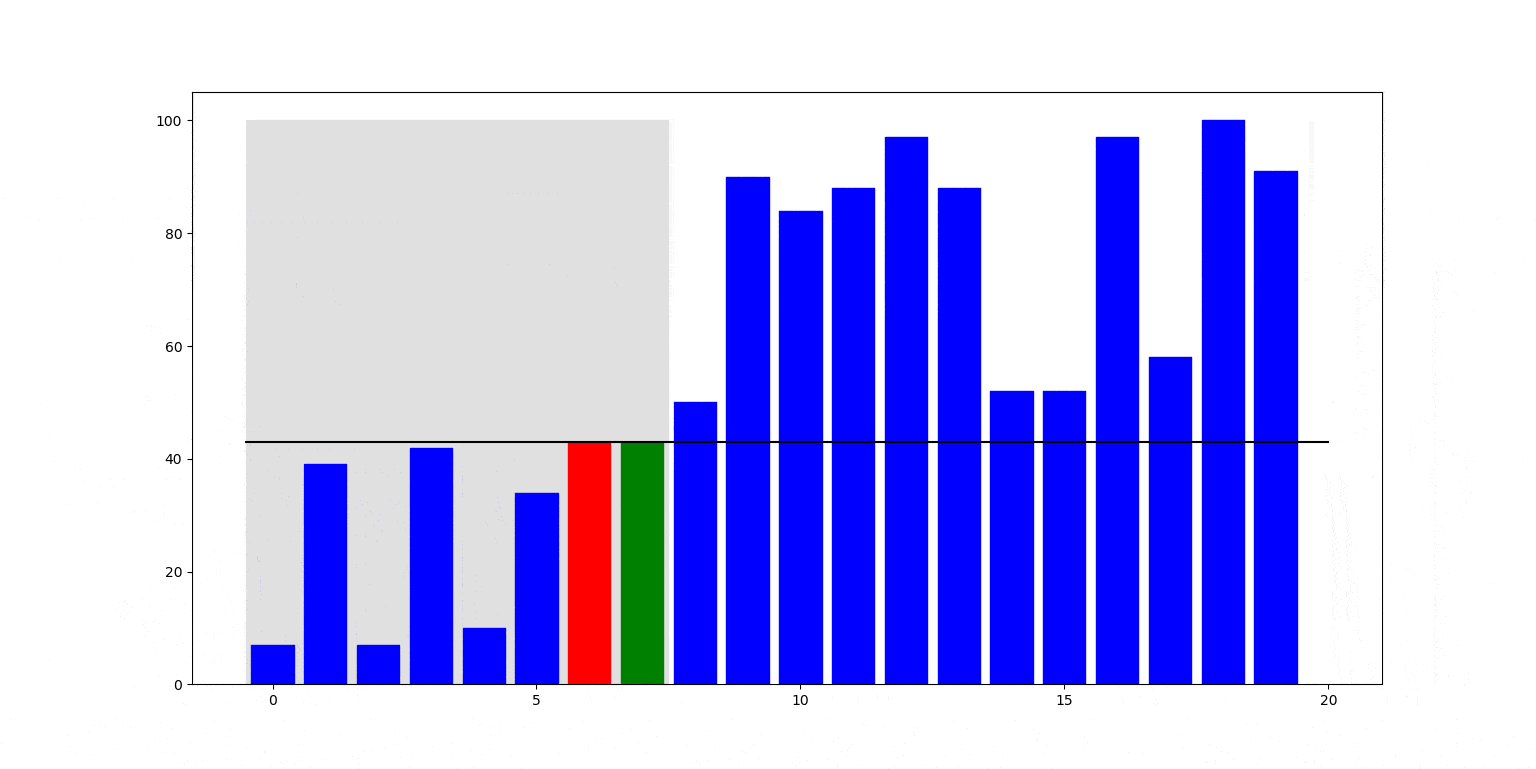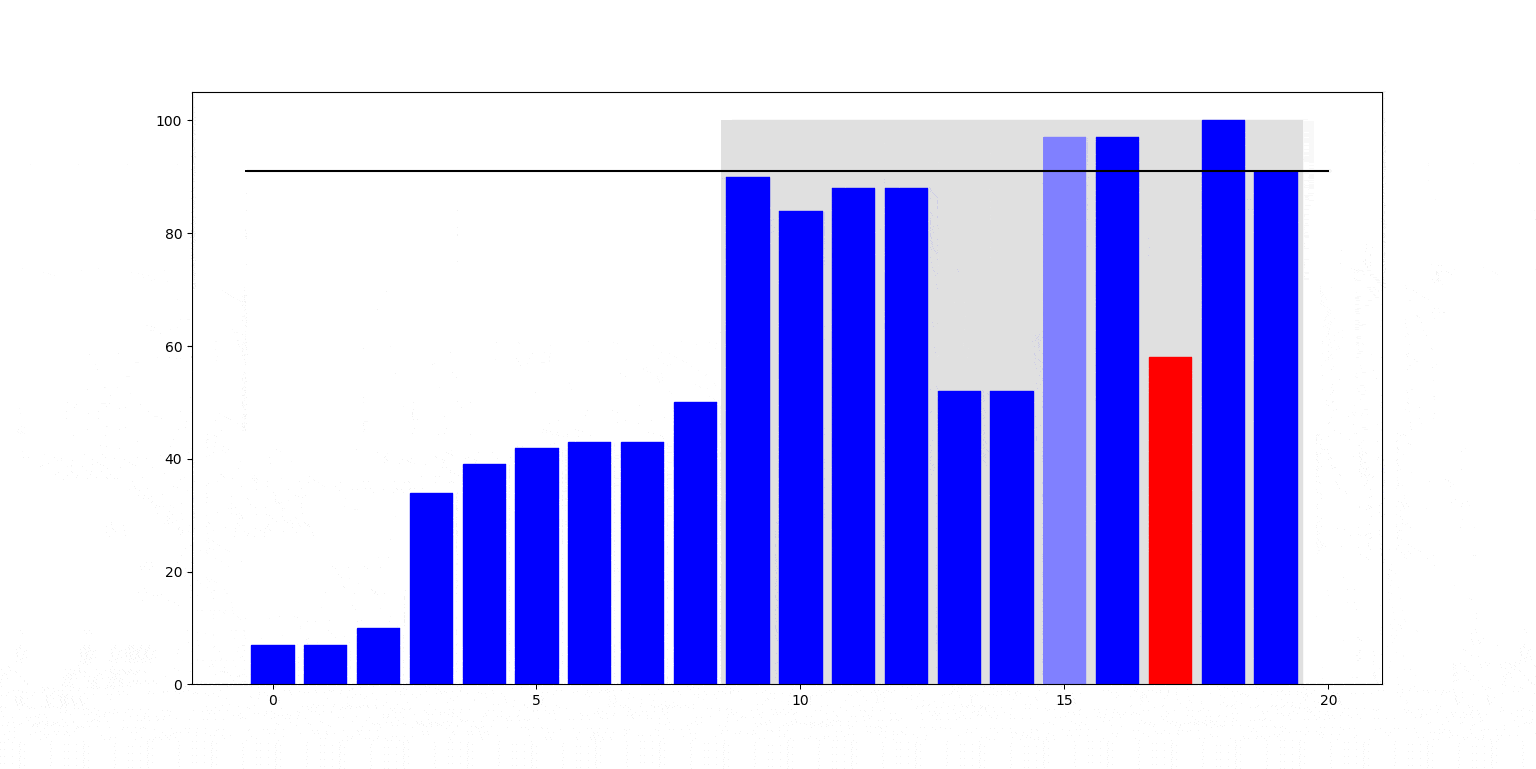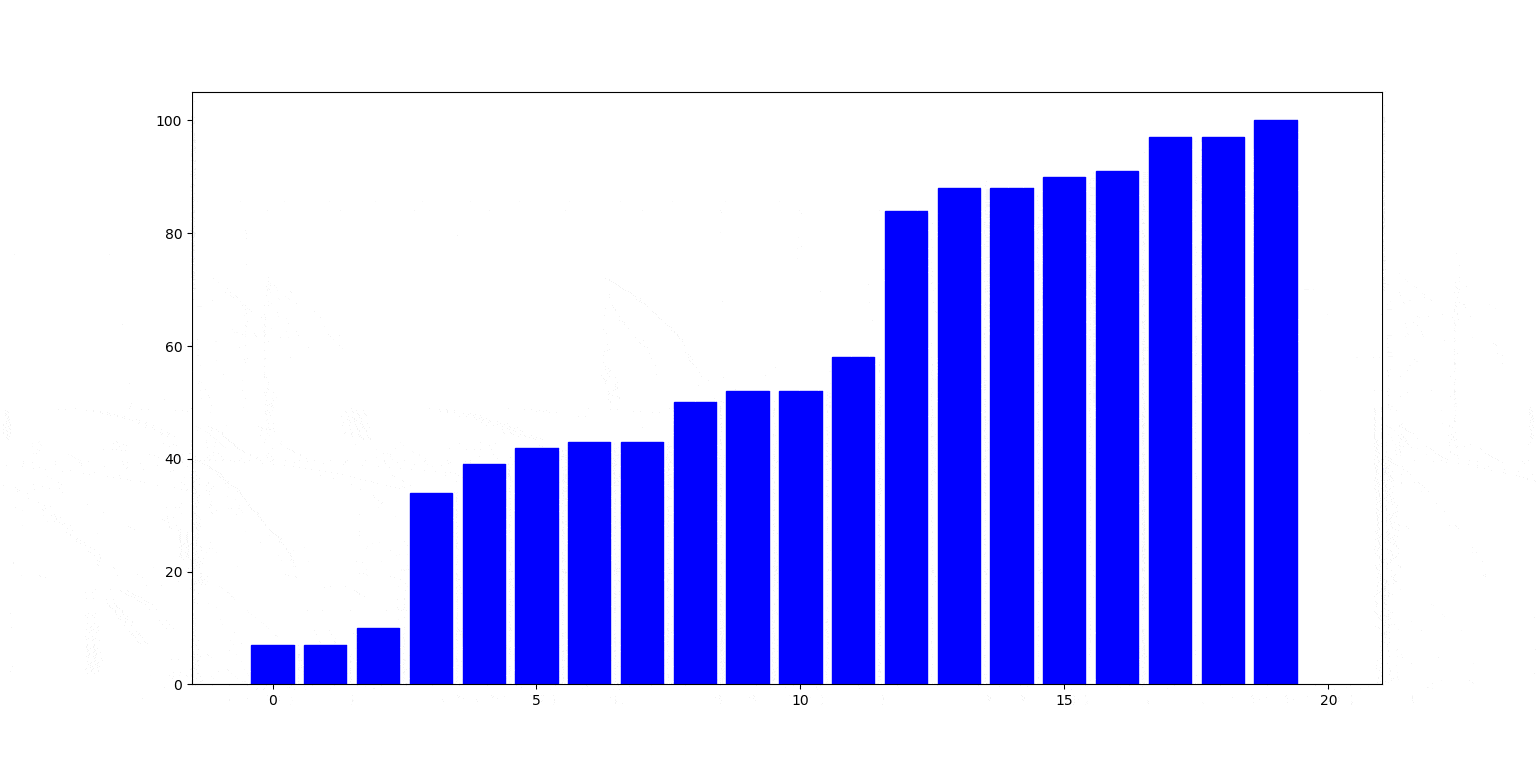
Cechy sortowania przez wstawianie:

Złożoność czasowa: Wydajność zależy od tego, w jaki sposób partycjonowanie fragmentów je dzieli. W przypadku optymistycznym i średnim, podział fragmentu dzieli go na dwie dostatecznie równe części, prowadząc do czasów $\Theta(n \log n)$. Jednak w przypadku pesymistycznym partycjonowanie wydziela fragment mniejszy jedynie o jeden od oryginalnego: dzieje się tak na przykład dla list już posortowanych (przypadek pesymistyczny). To degeneruje czas działania do $\Theta(n^2)$.
Złożoność pamięciowa: równa głębokości rekurencji. Średnio i optymistycznie: $\Theta(\log n)$, pesymistycznie $\Theta(n)$.
Stabilność: NIE. Partycjonowanie ma dość przypadkowy charakter i może przestawiać kolejność elementów równych według praporządku.

Algorytmy hybrydowe i podsumowanie ¶

Algorytmy typu "dziel i rządź" stanowią bazę wielu tzw. algorytmów hybrydowych. Polegają one na modyfikacji algorytmu w taki sposób, że zamiast redukować listy do posortowania do rozmiaru $0$ lub $1$, kończą tę redukcję gdy zajdzie pewien warunek. Następnie sortują tak zredukowane listy innym algorytmem.

Przykładem jest Timsort - algorytm, którego wariant implementuje metodę sort() w listach Pythona. Działa jak merge sort, który dla dostatecznie małych list (np. długości 30) przełącza się na insertion sort. Dla tak małych list, insertion sort działa w praktyce szybciej niż merge sort (mimo gorszej asymptotycznej złożoności obliczeniowej).

Innym przykładem jest Introsort, hybrydyzujący (w różnych wariantach) quicksort oraz heapsort (czasem też insertion sort). Efektem tej hybrydyzacji jest wydajny algorytm (zbliżony wydajnością do quicksorta), ale z gwarancją działania w czasie $\Theta(n \log n)$ w każdym przypadku.

Kończymy podsumowaniem cech algorytmów sortujących. W tabeli umieszczamy omówione algorytmy, oraz, dla porównania, Timsort, Introsort oraz, pozostawiony na przyszłość, Heapsort. Wszystkie czasy oraz złożoność pamięciowa podane są dokładnie (jako $\Theta(\cdot)$) dla przypadków optymistycznego (BEST), średniego (AVG) i pesymistycznego (WORST).

Algorytm	BEST	AVG	WORST	Pamięć	Stabilny
Selection sort	$n^2$	$n^2$	$n^2$	$1$	NIE
Insertion sort	$n$	$n^2$	$n^2$	$1$	TAK
Merge sort	$n \log n$	$n \log n$	$n \log n$	$n$[1]	TAK
Quicksort	$n \log n$	$n \log n$	$n^2$ [2]	$\log n$, $n$ [3]	NIE
Heapsort	$n \log n$	$n \log n$	$n \log n$	$1$	NIE
Timsort	$n$	$n \log n$	$n \log n$	$n$	TAK
Introsort	$n\log n$	$n\log n$	$n\log n$	$\log n$	NIE

Przypisy:
[1] - po modyfikacji "w miejscu" można zredukować złożoność pamięciową do $\log n$.
[2] - $n \log n$ po modyfikacjach.
[3] - średnio $\log n$, pesymistycznie $n$.