G. Jagiella | ostatnia modyfikacja: 11.03.2025 |
Kolejka - struktura danych podobna do stosu, gdzie obiekty są ułożone "jeden za drugim". Obsługuje co najmniej dwie operacje:
enqueue(x) - dokłada obiekt x na koniec kolejki.dequeue() - ściąga element z początku kolejki i zwraca go.enqueue(x) i dequeue() są odpowiednikami (odpowiednio) stosowych operacji push(x) i pop(). Kolejka dla wygody może obsługiwać też inne operacje (np. size(), is_empty(), peek()).
Naturalnym "życiowym" odpowiednikiem kolejki jest kolejka w sklepie.
Implemetancja kolejki znajduje się w pliku my_queue.py jako klasa Queue. Przypomina implementację stosu: elementy są wewnętrznie pamiętane na liście, gdzie początek kolejki znajduje się na końcu listy. Operacja enqueue(x) wkłada element pod zerowy indeks listy, wobec czego działa w czasie liniowo zależnym od rozmiaru listy. W dalszej części skryptu (w tym rozdziale i następnym) omówimy alternatywne, lepsze implementacje.
Rozważmy myjnię samochodową. Do myjni przyjeżdzają brudne samochody, wymagające mycia przez pewną ilość minut. Gdy samochód przyjeżdza, a myjnia jest wolna, samochód zajmie ją na stosowną ilość minut. W przeciwnym wypadku stanie w kolejce. Gdy myjnia zwalnia się, zajmuje je pierwszy samochód w kolejce.
Nasz cel to zasymulowanie takiego procesu i zbadanie, ile wynosi średni czas oczekiwania samochodu na wolne stanowisko.
Bardziej algorytmicznie: naszą symulację będziemy prowadzić w jednominutowych odstępach. Na początku myjnia jest wolna, a kolejka samochodów jest pusta. Tworzymy następujące klasy:
Car - reprezentuje samochód. Gdy jest tworzony, posiada pewną ilość "brudu" (losowa liczba całkowita z przedziału [1, 5]), czyli ilości minut, potrzebnych do umycia samochodu. Pamięta także czas, w którym został stworzony (będzie to czas, w którym przyjechał do myjni).
CarWash - reprezentuje myjnię. Myjnia jest wolna lub zawiera aktualnie myty samochód.
Myjnia (opis bez szczegółów implementacji)
Parametrami symulacji są: liczba minut $n$, oraz szansa $r \in [0, 1]$ na to, że w danej minucie przyjedzie samochód.
Symulację prowadzimy w odstępach jednej minuty przez $n$ minut. W każdej minucie wykonujemy kolejne kroki:
- Najpierw losujemy, czy przyjechał samochód (z szansą $r$). Jeśli tak, kładziemy go do kolejki.
- Jeśli myjnia jest pusta, a w kolejce stoją samochody: usuwamy samochód z kolejki i kładziemy go do myjni.
- Myjnia, jeśli nie jest pusta, dokonuje jednominutowego mycia samochodu.
Następnie algorytm możemy modyfikować: jeśli każdy samochód nowuje czas, w jakim stanął w kolejce, możemy sprawdzić czas oczekiwania na mycia w momencie, gdy wkładamy samochód do myjni w kroku 2). Na zakończenie symulacji, możemy wyciągnąć średnią tych czasów.
Kody klas Car i CarWash:
import random
class Car:
def __init__(self, timestamp):
self.timestamp = timestamp
self.dirt = random.randrange(1, 6)
def wash(self):
self.dirt -= 1
def is_clean(self):
return self.dirt <= 0
def get_dirt(self):
return self.dirt
def waiting_time(self, current_time):
return current_time - self.timestamp
class CarWash:
def __init__(self):
self.current_car = None
def tick(self):
if self.current_car is None:
return
self.current_car.wash()
if self.current_car.is_clean():
self.current_car = None
def busy(self):
return self.current_car is not None
def __str__(self):
if not self.busy():
return "Car wash: idle"
return "Car wash: cleaning car, {} dirt remaining".format(self.current_car.get_dirt())
def start_next(self, new_car):
self.current_car = new_car
Oraz kod samej symulacji:
import random
from my_queue import Queue
# ! Odkomentować poza notebookiem:
# from car import Car
# from carwash import CarWash
def simulate_car_wash(num_minutes, chance):
car_wash = CarWash()
queue = Queue()
total_time = 0
total_cars = 0
for cur_minute in range(num_minutes):
if random.random() < chance:
new_car = Car(cur_minute)
queue.enqueue(new_car)
print('queued a new car with {} dirt'.format(new_car.get_dirt()))
if not car_wash.busy() and not queue.is_empty():
new_car = queue.dequeue()
car_wash.start_next(new_car)
total_cars += 1
total_time += new_car.waiting_time(cur_minute)
print('started to wash a car with {} dirt'.format(new_car.get_dirt()))
print("Time: {} minutes, queued cars: {}".format(cur_minute, queue.size()))
print(str(car_wash))
car_wash.tick()
print("avg waiting time: {} m".format(total_time / total_cars))
simulate_car_wash(30, 0.2)
Time: 0 minutes, queued cars: 0 Car wash: idle Time: 1 minutes, queued cars: 0 Car wash: idle Time: 2 minutes, queued cars: 0 Car wash: idle Time: 3 minutes, queued cars: 0 Car wash: idle queued a new car with 3 dirt started to wash a car with 3 dirt Time: 4 minutes, queued cars: 0 Car wash: cleaning car, 3 dirt remaining Time: 5 minutes, queued cars: 0 Car wash: cleaning car, 2 dirt remaining queued a new car with 3 dirt Time: 6 minutes, queued cars: 1 Car wash: cleaning car, 1 dirt remaining started to wash a car with 3 dirt Time: 7 minutes, queued cars: 0 Car wash: cleaning car, 3 dirt remaining Time: 8 minutes, queued cars: 0 Car wash: cleaning car, 2 dirt remaining Time: 9 minutes, queued cars: 0 Car wash: cleaning car, 1 dirt remaining queued a new car with 3 dirt started to wash a car with 3 dirt Time: 10 minutes, queued cars: 0 Car wash: cleaning car, 3 dirt remaining Time: 11 minutes, queued cars: 0 Car wash: cleaning car, 2 dirt remaining queued a new car with 4 dirt Time: 12 minutes, queued cars: 1 Car wash: cleaning car, 1 dirt remaining started to wash a car with 4 dirt Time: 13 minutes, queued cars: 0 Car wash: cleaning car, 4 dirt remaining Time: 14 minutes, queued cars: 0 Car wash: cleaning car, 3 dirt remaining queued a new car with 3 dirt Time: 15 minutes, queued cars: 1 Car wash: cleaning car, 2 dirt remaining Time: 16 minutes, queued cars: 1 Car wash: cleaning car, 1 dirt remaining started to wash a car with 3 dirt Time: 17 minutes, queued cars: 0 Car wash: cleaning car, 3 dirt remaining Time: 18 minutes, queued cars: 0 Car wash: cleaning car, 2 dirt remaining Time: 19 minutes, queued cars: 0 Car wash: cleaning car, 1 dirt remaining Time: 20 minutes, queued cars: 0 Car wash: idle Time: 21 minutes, queued cars: 0 Car wash: idle Time: 22 minutes, queued cars: 0 Car wash: idle Time: 23 minutes, queued cars: 0 Car wash: idle Time: 24 minutes, queued cars: 0 Car wash: idle Time: 25 minutes, queued cars: 0 Car wash: idle queued a new car with 2 dirt started to wash a car with 2 dirt Time: 26 minutes, queued cars: 0 Car wash: cleaning car, 2 dirt remaining Time: 27 minutes, queued cars: 0 Car wash: cleaning car, 1 dirt remaining queued a new car with 1 dirt started to wash a car with 1 dirt Time: 28 minutes, queued cars: 0 Car wash: cleaning car, 1 dirt remaining Time: 29 minutes, queued cars: 0 Car wash: idle avg waiting time: 0.5714285714285714 m
Pytanie: dla jakiego parametru $r$ należy spodziewać się, że kolejka będzie rosnąć (tj. myjnia jest przepełniona)?
Myjnia myje "minutę brudu na minutę", a brudu pojawia się średnio $3r$ na minutę, zatem można spodziewać się, żę krytyczną wartością $r$ jest $1/3$.
Możliwe ulepszenia kodu: więcej myjni (stanowisk myjących) obsługujących tę samą kolejkę? Różna wydajność tych myjni? Wybór rozdzielczości symulacji (np. sekunda zamiast minuty)?
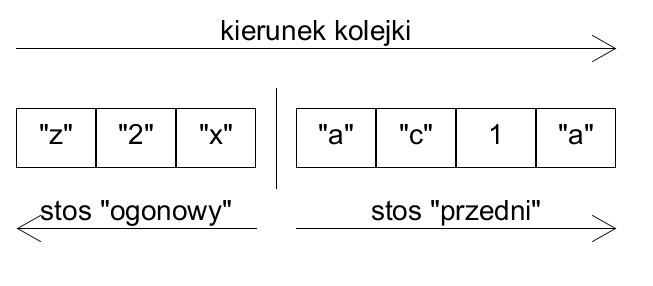
"Właściwą" implementację kolejki omówimy w następnym rozdziale skryptu. W tym podrozdziale omówimy działanie alternatywnej implementacji, wykonanej z pomocą pary stosów: "przedniego" i "ogonowego". Elementami w kolejce są elementy leżące w jednym z tych stosów. Dla elementów leżących w stosie "ogonowym", element bliżej jego szczytu stoi dalej w kolejce. Dla elementów leżących w stosie "przednim" jest odwrotnie. Dodatkowo, elementy w stosie "przednim" stoją w kolejce przed elementami w stosie "ogonowym".
Przykładowo, kolejka o elementach "z", "2", "x", "a", "c", 1, "a" (gdzie "z" jest na końcu kolejki) może być zareprezentowana następującymi stosami, gdzie T oznacza stos "ogonowy" (tail) a H stos "przedni" (head):
T: "x", "2", "z"
H: "a", "c", 1, "a"
Na rysunku:

Ta sama kolejka może być reprezentowana również na każdy z poniższych sposobów:
T: "2", "z"
H: "x", "a", "c", 1, "a"
lub [1]
T: "z", "2", "x", "a", "c", 1, "a"
H:
lub [2]
T:
H: "a", 1, "c", "a", "x", "2", "z"
Zauważmy przy tym, że aby przemienić reprezentację [1] na reprezentację [2], wystarczy elementy stosu "ogonowego" przenieść na stos "przedni" za pomocą operacji stosowych:
T jest niepusty, wykonujemy H.push(T.pop())Operacje enqueue(x) i dequeue() implementujemy na kolejce Q następująco:
Q.enqueue(x) tłumaczymy na T.push(x)..Q.dequeue() (na niepustej kolejce) implementujemy następująco:H jest pusty, przenosimy elementy stosu T na stos H (zgodnie z opisem powyżej),H.pop().W takiej implementacji, operacja enqueue(x) zawsze wykonuje się w czasie stałym. Czas wykonania dequeue() zależy jednak od przypadku: często będzie to czas stały, jednak w przypadku, gdy H jest pusty, operacja ta wykona się w czasie liniowo zależnym od liczby elementów w kolejce (dla każdego z nich wykonujemy parę operacji stosowych pop() i push(x)). Możemy jednak rozważyć sytuację, w której wykonujemy wiele operacji enqueue(x) i dequeue() i rozważyć ich uśredniony czas działania (uwaga: to nie jest to samo, co czas uśredniony w rozumieniu pierwszego rozdziału skryptu).
Przypuśćmy, że pewien algorytm kładzie i wyciąga z kolejki $n$ elementów, w nieznanej kolejności (czyli może umieścić w niej kilka elementów, następnie kilka z nich wyciągnąć, znów włożyć kilka elementów, etc.). Zbadajmy, ile w sumie zostanie wykonanych operacji stosowych. W tym celu rozważmy całkowitą liczbę operacji użytych do włożenia i wyciągnięcia danego elementu:
push(x).pop() i push(). Stanie się to w momencie wyciągania z kolejki pewnego jej elementu (ale niekoniecznie tego samego).pop().Stąd, w sumie dla $n$ elementów zostaną wykonane dwie operacje stosowe push(x) i dwie operacje stosowe pop(x), czyli $4n$ operacji elementarnych. Zatem złożoność algorytmu (licząc jedynie operacje wykonane na kolejce) jest klasy $\Theta(n)$, czyli lepsza, niż w pesymistycznym przypadku dla implementacji wykładowej (która wynosi $\Theta(n^2)$).