G. Jagiella | ostatnia modyfikacja: 06.03.2021 |
Wykład 2 (cz. 2): stos i jego zastosowania¶
Struktury danych¶
Struktura danych to sposób organizacji danych w pamięci komputera.
Struktury danych pozwalają na przechowywanie obiektów w pamięci oraz wykonywanie na nich pewnych operacji, takich jak: umieszczanie w strukturze nowych obiektów lub usuwanie ich; sprawdzanie, czy obiekt jest elementem struktury; iteracja po obiektach w strukturze; indeksowanie (czyli wybieranie obiektu spod danego indeksu bądź klucza); etc.
Znanymi już, wbudowanymi w Pythona strukturami danych są listy, zbiory, słowniki i krotki.
Struktury danych (a właściwie ich konkretne implementacje) gwarantują też asymptotyczne czasy działania operacji na nich. Struktury różnią się dostępnymi operacjami, oraz czasami ich działania. Nie istnieje "uniwersalna" struktura danych pozwalająca na wszystkie możliwe operacje i jednocześnie gwarantująca najlepsze czasy działania tych operacji. Zamiast tego, każda struktura jest efektem pewnych kompromisów między czasami konkretnych operacji, rozmiarem pamięci jaki struktura zajmuje, etc. Wady i zalety struktury determinują jej przydatność w konkretnych algorytmach.
Przykładowo: lista może zostać użyta w zastępstwie zbioru, jednak czas operacji x in s dla list jest liniowy, a nie stały jak w przypadku zbioru. Z drugiej strony, lista pozwala na utrzymywanie obiektów w żądanej kolejności.
Stos¶
Jedną z najbardziej elementarnych struktur danych w informatyce jest stos. Reprezentuje on kolekcję obiektów ułożonych "jeden na drugim" (jak stos książek). Obiekty można dodawać na szczyt stosu i ściągać ze szczytu stosu. Obiekt włożony na stos jako ostatni zostanie z niego wyciągnięty jako pierwszy (tzw. struktura LIFO - last in, first out).
Struktury danych reprezentujemy na ogół jako klasy, a operacje na nich jako ich metody (w tym metody specjalne, definiujące działania operatorów etc.). Stos obsługuje co najmniej dwie operacje (tu zapisane jak metody):
push(x)- kładzie obiektxna szczycie stosu.pop()- ściąga obiekt ze szczytu stosu i zwraca go.
Dla wygody, stos może obsługiwać dodatkowe operacje, na przykład:
peek()- zwraca (bez usuwania) obiekt ze szczytu stosu.size()- zwraca ilość obiektów na stosie.is_empty()- orzeka, czy stos jest pusty.
Implementacje stosu¶
Stos zdefiniowaliśmy przez jego interfejs - zestaw operacji, jakie można na nim wykonać. Interfejs nie wspomina o konkretnej implementacji tej struktury danych. Na potrzeby wykładu, zaimplementujemy stos jako klasę (plik stack.py w materiałach do wykładu) z odpowiednimi metodami.
Wewnętrznie, klasa reprezentująca stos będzie przetrzymywać obiekty ze stosu na (początkowo pustej) liście, pamiętanej jako atrybut items. Obiekty będą występować na liście zgodnie z kolejnością na stosie. Musimy jednak zdecydować, czy lista reprezentuje stos "z dołu do góry", czy "z góry na dół": to znaczy, czy element ze szczytu stosu będzie ostatnim, czy pierwszym elementem listy.
Zamiast wybierać, zaimplementujemy stos na oba sposoby - odpowiednio jako klasy Stack i Stack1, a następnie porównamy obie implementacje.
- W klasie
Stack, dołożenie elementu na szczyt stosu odpowiada dołożeniu elementu na koniec listy, a więc operacjiappend(x). Analogicznie, usunięcie elementu ze szczytu odpowiada operacjipop(). Operacje te wykonują się w czasie klasy $\Theta(1)$. - W klasie
Stack1, dołożenie elementu na szczyt odpowiada listowej operacjiinsert(0, x)(wstawienie elementu pod indeks0), natomiast usunięcie - operacjipop(0). Czasy tych operacji są klasy $\Theta(n)$, gdzie $n$ to rozmiar stosu.
Implementacje peek() są podobne w obu implementacjach, a size() i is_empty() są wręcz identyczne. Wszystkie te działania wymagają $\Theta(1)$ operacji. Pełna treść obu implementacji:
class Stack:
def __init__(self):
self.items = []
# Θ(1)
def is_empty(self):
return self.items == []
# Θ(1)
def push(self, item):
self.items.append(item)
# Θ(1)
def pop(self):
return self.items.pop()
# Θ(1)
def peek(self):
return self.items[-1]
# Θ(1)
def size(self):
return len(self.items)
# alternatywna implementacja stosu
class Stack1:
def __init__(self):
self.items = []
# Θ(1)
def is_empty(self):
return self.items == []
# Θ(n)
def push(self, item):
self.items.insert(0, item)
# Θ(n)
def pop(self):
return self.items.pop(0)
# Θ(1)
def peek(self):
return self.items[0]
# Θ(1)
def size(self):
return len(self.items)
Poniżej krótki test prezentujący działanie stosu:
s = Stack() # s -> []
print(s.is_empty())
s.push(4) # s -> [4]
s.push("pies") # s -> [4, 'pies']
print(s.peek())
s.push(True) # s -> [4, 'pies', True]
print(s.size())
print(s.is_empty())
s.push(8.4) # s -> [4, 'pies', True, 8.4]
print(s.pop()) # s -> [4, 'pies', True]
print(s.pop()) # s -> [4, 'pies']
print(s.size())
Porównanie wydajności implementacji¶
Klasy Stack i Stack1 mają identyczny interfejs, a znaczenie odpowiednich metod jest takie samo dla obu klas. Są więc one w pewnym sensie nieodróżnialne z punktu widzenia użytkownika: mogą być używane wymiennie w algorytmach. Gwarantują jednak inne czasy działania niektórych operacji. Ma to konsekwencje dla czasu działania implementacji algorytmów, w których są używane. Rozważmy funkcję:
def f(n):
s = Stack()
for i in range(n):
s.push(i)
while not s.is_empty():
s.pop()
Dla pierwszej implementacji stosu, czas działania takiej funkcji jest klasy $\Theta(n)$. Dla drugiej implementacji, będzie to $\Theta(n^2)$. Możemy to potwierdzić eksperymentalnie, jak w poprzednim podrozdziale (można przy tym zwrócić uwagę, że gdyby zastąpić operacje push i pop przez kryjące się pod nimi operacje listowe, jest to przykład niemal identyczny z tym z podrozdziału "Eskperyment" poprzedniego rozdziału skryptu). Zmierzone czasy wywołania f(n) używającej Stack dla $n = 0, 1000, \ldots, 30000$, oraz dopasowana do niej funkcja liniowa wyglądają na wykresie następująco:
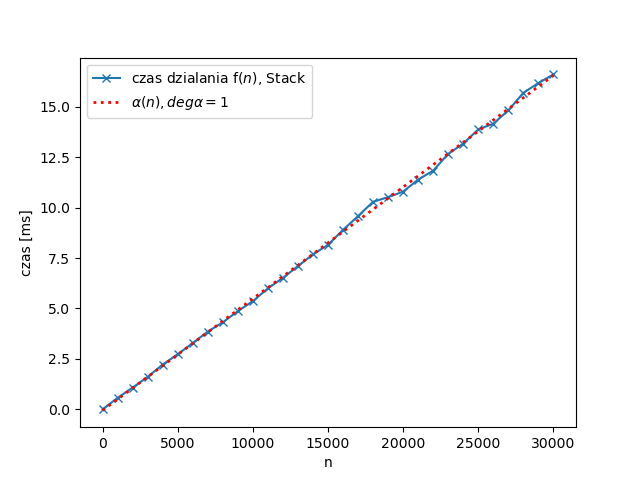
Analogiczny wykres, gdzie Stack zostało zastąpione przez Stack1, a funkcja liniowa kwadratową:
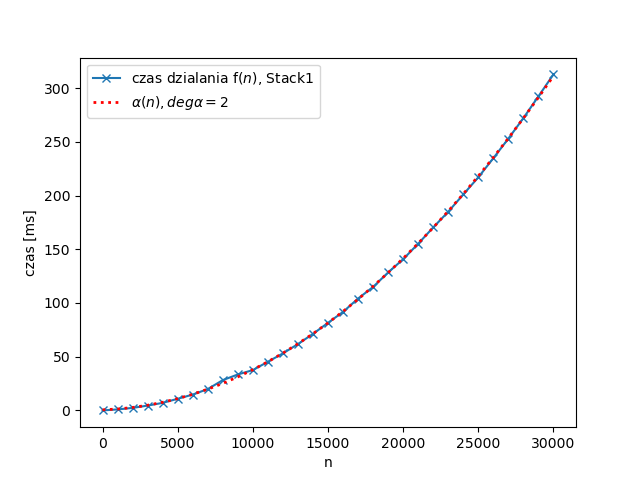
Zastosowania stosu¶
Stos, jako jedna z fundamentalnych struktur danych, pojawia się powszechnie jako podstawowa "cegiełka" wielu algorytmów.
Wybrane przykłady¶
Poniżej podajemy kilka wybranych zastosowań stosu w informatyce (tudzież technologii informacyjnej) - niektóre z nich omówimy dokładniej.
I. Cofanie zmian w edytorach. Edytory tekstu, grafiki etc. pozwalają zazwyczaj na cofanie wprowadzanych zmian (ctrl+z). Mechanizm ten polega na notowaniu każdej dokonanej przez użytkownika zmiany względem oryginalnego (np. pustego) dokumentu, przykładowo:
- wprowadzenia pojedynczej litery,
- wklejenia kawałka tekstu w wybrane miejsce
- usunięcia kawałka tekstu,
- przesunięcia fragmentu obrazka,
wraz z informacją potrzebną do anulowania tej zmiany, odpowiednio na przykład:
- indeksu wprowadzonej litery,
- indeksu wklejonego fragmentu wraz z jego długością,
- indeksu, z którego został usunięty kawałek tekstu, oraz sam kawałek,
- przesunięty fragment, wektor przesunięcia, i ewentualna informacja o innych fragmentach, które zostały zasłonięte (lub w inny sposób utracone) w wyniku przesunięcia.
Każda zanotowana w ten sposób zmiana zostaje położona na stos. Cofnięcie zmiany polega na ściągnięciu informacji o zmianie ze stosu i wykonaniu operacji przeciwnej. Kolejne cofnięcie anuluje zmianę poprzednią.
II. Wstecz/dalej w przeglądarkach internetowych. Przeglądarka przechowuje na stosie adresy odwiedzanych stron. Przejście do nowej strony kładzie na stos adres aktualnie opuszczanej strony. Operacja "wstecz" ściąga ten adres ze stosu i przechodzi do tego adresu. Jednocześnie operacja "wstecz" może odłozyć adres opuszczanej strony na drugi stos, używany w analogicznie sposób przez operację "dalej".
III. Problem weryfikacja nawiasowania, który omówimy nieco szerzej w następnych podrozdziałach wraz z jego uogólnieniami: parsowanie plików HTML, XML, $\LaTeX$ i innych.
IV. Parsowanie i wyliczanie wyrażeń arytmetycznych.
V. Wyrażanie liczby w zadanym systemie liczbowym, omówione w dalszym podrozdziale.
Weryfikacja poprawności nawiasowania¶
Prostym zastosowaniem stosu jest problem sprawdzania poprawnego nawiasowania, który pokażemy w dwóch wersjach, a następnie opiszemy jego praktyczne uogólnienie i zastosowanie do parsowania dokumentów różnych formatów. Rozważmy napisy złożone (wyłącznie) z okrągłych nawiasów otwierających i zamykających: (, ). Napis taki nazwiemy poprawnie znawiasowanym, gdy jednocześnie:
- Każdy nawias otwierający jest zamknięty przez nawias zamykający.
- Każdy nawias zamykający zamyka pewien nawias otwierający.
Poprawnie znawiasowanymi są na przykład napisy (()()), (())()() i ((())). Niepoprawnie znawiasowane są natomiast ((), ()), )(.
Poprawność nawiasowania możemy zbadać sprawdzając, czy każdy kolejny nawias zamykający "znosi się" z nawiasem otwierającym, oraz czy po zniesieniu wszystkich par takich nawiasów nie pozostaje żaden niesparowany nawias otwierający. Przykładowo, dla napisu (()()), kolejne kroki weryfikacji wyglądają następująco:
(()()) - napis początkowy
(()()) - para nawiasów, które ze sobą znosimy.
(()) - napis po zredukowaniu.
(()) - kolejna znosząca się nawzajem para nawiasów.
()
() - ostatnia znosząca się para
brak nawiasów, napis jest poprawnie znawiasowany.
Z kolei dla napisu (() mamy:
(() - napis początkowy
(()
( - nawias, który nie ma pary; napis nie jest poprawnie znawiasowany
Procedurę znoszenia nawiasów możemy usystematyzować, badając kolejne nawiasy występujące w napisie po kolei, od lewej do prawej, według następującego algorytmu:
Kroki weryfikacji poprawności nawiasowania (wejście - ciąg nawiasów
(i)):
- Stwórz pusty stos. Na stos będziemy odkładać nawiasy
(.- Dla każdego nawiasu z wejścia:
2a. Jeśli nawiasem jest(, odłóż go na stos.
2b. Jeśli nawiasem jest): ściągnij nawias(ze stosu (znosząc go z właśnie odczytanym nawiasem). Jeśli stos jest pusty, to przeczytany nawias)nie zamyka żadnego nawiasu, więc zwróćFalse.- Po wyczerpaniu nawiasów z wejścia, sprawdź czy stos jest pusty i zwróć
Truejeśli tak,Falsew przeciwnym wypadku (jeśli stos nie jest pusty, to nawiasy(które w nim są nie są sparowane).
Poniższe animacje demonstrują działanie algorytmu: dla napisu (()()):

Dla napisu (())()):

Oraz dla napisu (()():

Opisany wyżej algorytm przekładamy na kod, w którym używamy klasy Stack jako stosu:
def check_parens(sequence):
s = Stack()
for c in sequence:
if c == '(':
s.push(c)
elif c == ')':
if s.is_empty():
return False
else:
s.pop()
return s.is_empty()
Sprawdzamy działanie funkcji na przykładach:
print(check_parens('(())'))
print(check_parens('(())()'))
print(check_parens('())'))
print(check_parens('((()()))'))
Czynimy teraz dwie uwagi:
- Zamiast klasy
Stack, w kodzie możemy po prostu użyć list (nasza implementacja stosu to jedynie "nakładka" na listę i operacje na niej). Użycie tej klasy podkreśla jednak dla czytelnika kodu, że algorytm używa konkretnej struktury danych - stosu, a nie listy "ogólnego zastosowania". Wskazuje też od razu, jakie operacje będą wykonywane na strukturze, co ułatwia rozumienie kodu. - Możemy zauważyć, że analogiczny algorytm moglibyśmy zaimplementować bez użycia stosu. Jedyną informacją, jaką dostarcza nam stos jest liczba otwartych nawiasów, która zwiększa się o $1$ po napotkaniu nawiasu otwierającego, i zmniejsza o $1$ po napotkaniu nawiasu zamykającego. Moglibyśmy zatem zastąpić stos licznikiem "aktualnie otwartych" nawiasów, zmieniając jego wartość po każdym przeczytanym nawiasie wejścia. Napis jest poprawnie znawiasowany dokładnie wtedy, gdy taki licznik zawsze przyjmuje nieujemną wartość, a jego koncową wartością jest $0$.
Zasadność użycia stosu zamiast prostego licznika otwartych nawiasów okaże się w następnym podrozdziale, w którym rozważymy drobną modyfikację problemu poprawnego nawiasowania.
Weryfikacja poprawności nawiasowania II¶
Załóżmy teraz, że rozważamy napisy złożone z nawiasów otwierających (, [ i { oraz odpowiadających im nawiasów zamykających ), ] i }. Napis potraktujemy jako poprawnie znawiasowany, gdy spełnia warunki z poprzedniego podrozdziału, przy dodatkowym warunku, że nawiasy otwierające są sparowane z odpowiadającymi im nawiasami zamykającymi. Poprawnie znawiasowane są zatem: [(){}], ()[][]{} oraz {()}, a niepoprawnie: {), {(){}] i [][][]{].
Weryfikacja poprawności takiego napisu jest drobną modyfikacją poprzedniego sposobu:
Kroki weryfikacji poprawności nawiasowania II (wejście - ciąg nawiasów spośród
([{)]}):
- Stwórz pusty stos. Na stos będziemy odkładać nawiasy otwierające.
- Dla każdego nawiasu z wejścia:
2a. Jeśli nawias jest otwierający, odłóż go na stos.
2b. Jeśli nawias jest zamykający: ściągnij nawias otwierający ze stosu. Jeśli nie pasuje on do przeczytanego nawiasu zamykającego lub stos jest pusty, zwróćFalse.- Po wyczerpaniu nawiasów z wejścia, sprawdź czy stos jest pusty i zwróć
Truejeśli tak,Falsew przeciwnym wypadku.
Ponownie pokazujemy animacje działania algorytmu. Dla napisu ({}[]):

Dla napisu ({)[]):

Oraz dla napisu ({}[]}:

W poniższej implementacji algorytmu używamy pomocniczej funkcji matches(left, right), rozstrzygającej, czy para nawiasów left i right do siebie pasuje:
def check_parens2(sequence):
s = Stack()
for c in sequence:
if c in '({[':
s.push(c)
elif c in ')}]':
if s.is_empty():
return False
else:
left = s.pop()
if not matches(left, c):
return False
return s.is_empty()
def matches(left, right):
pairing = {'(': ')', '[': ']', '{': '}'}
return pairing[left] == right
Całość kończymy testami:
print(check_parens2('{{([][])}()}'))
print(check_parens2('[{()]'))
W tym algorytmie, stos rzeczywiście okazuje się potrzebny - samo śledzenie liczby otwartych nawiasów (każdego rodzaju) nie wystarcza, gdyż znaczenie ma też ich kolejność.
Uwaga o parsowaniu dokumentów¶
Zaprezentowany w poprzednich podrozdziałach algorytm weryfikacji poprawności nawiasowania uogólnia się do algorytmu weryfikacji struktury dokumentów w różnych formatach. Przykładowo: w uproszczeniu, dokument HTML (lub XML) składa się z sekwencji tagów otwierających postaci <tag> i pasujących do nich tagów postaci </tag>. Przykładowymi takimi parami są <html> i </html>; <body> i </body>; <b> i </b>. Pomiędzy tagami (lub jako pewne parametry samych tagów) mogą znajdować się dodatkowe informacje. W poprawnie sformowanym dokumencie HTML lub XML, każdy tag otwierający jest sparowany odpowiednim tagiem zamykającym. Algorytm weryfikujący, czy dokument jest dobrze sformowany to dokładnie algorytm poprawności weryfikacji nawiasowania, gdzie "nawiasem" jest każdy tag.
Podobnej weryfikacji poddają się inne ustrukturyzowane dokumenty, np $\LaTeX$.
Zapis liczby w zadanej podstawie¶
Ostatnim (w tym rozdziale) zastosowaniem stosu będzie algorytm reprezentowania liczby naturalnej dodatniej w wybranej podstawie liczbowej. Skorzystamy z własności, że elementy wkładane do stosu są z niego wyciągane w odwrotnej kolejności.
Rozważmy liczbę całkowitą $n > 0$. Wtedy:
- Reszta z dzielenia tej liczby przez $2$ to jej ostatnia cyfra zapisu binarnego.
- Iloraz całkowity $n$ przez $2$ odpowiada liczbie powstałej przez wykreślenie jej ostatniej cyfry zapisu binarnego.
Korzystając z powyższych własności, naprzemienne wyznaczanie reszty z dzielenia $n$ przez $2$ oraz zastępowanie $n$ przez jej całkowity iloraz przez $2$ aż do uzyskania $0$ pozwala na wyodrębnienie kolejnych (od końca) cyfr zapisu binarnego $n$.
Przykładowo, dla $n = 19_{(10)} = 10011_{(2)}$:
19 % 2 == 1 (ostatnia cyfra)
19 // 2 == 9 (binarnie: 1001
9 % 2 == 1 (przedostatnia cyfra)
9 // 2 == 4 (binarnie: 100
4 % 2 == 0 (trzecia cyfra od końca)
4 // 2 == 2 (binarnie: 10
2 % 2 == 0 (czwarta cyfra od końca)
2 // 2 == 1 (binarnie: 1
1 % 2 == 1 (piąta cyfra od końca)
1 // 2 == 0 (koniec)
Cyfry uzyskane w krokach polegających na braniu reszty z dzielenia możemy kłaść na stos, a po zakończeniu procesu ściągnąć je po kolei ze stosu, rekonstruując binarny zapis $n$ we właściwej kolejności. Przykładowa implementacja:
def change_base_bin(n):
s = Stack()
while n > 0:
r = n % 2
s.push(r)
n = n // 2
result = ""
while not s.is_empty():
result += str(s.pop())
return result
Z przykładowymi wynikami:
print(change_base_bin(19))
print(change_base_bin(1025))
print(change_base_bin(2653453456346))
Analogicznie możemy znaleźć reprezentację $n$ w innych systemach liczbowych, zmieniając w algorytmie dzielnik $2$ na podstawę systemu.