G. Jagiella

Skrypt do wykładu Programowanie 2 (Python)

ostatnia modyfikacja: 05.03.2021

Wykład 2 (cz. 1): złożoność obliczeniowa, c.d.

Spis treści

Wyznaczanie złożoności fragmentów kodu

W tym rozdziale skryptu uzupełnimy odpowiedź na pytanie, które instrukcje zliczamy przy wyznaczaniu złożoności obliczeniowej. Dokonamy też analizy złożoności kilku fragmentów kodu, demonstrując standardowe techniki takich analiz. Zbadamy następnie czasy operacji na standardowych kolekcjach Pythona, ze szczególnym uwzględnieniem list. Rozdział zakończymy uwagami na temat ograniczeń, jakim podlega analiza złożoności algorytmów, oraz na temat konwencji.

W niektórych szczególnych problemach, w algorytmach je rozwiązujących dominuje pewien rodzaj operacji (przykładowo: mnożenie pojedynczych współczynników w algorytmach mnożenia macierzy$^1$; operacja porównania w algorytmach sortujących). Analizując algorytmy skupiamy się wtedy na zliczaniu tylko takich operacji. Domyślnie jednak, analizując algorytmy bądź fragmenty kodu, zliczamy wszystkie operacje. Niektóre z nich przyjmujemy jako elementarne i wykonywane w czasie stałym, w szczególności:

  • Operacje arytmetyczne na liczbach$^2$ i logiczne.
  • Porównania prostych obiektów (liczb, krótkich napisów).
  • Przypisania.
  • Wywoływanie funkcji.
  • Przejście do następnej linijki kodu, do następnej iteracji pętli while/for, lub wstapienie do bloku.
  • (dość specyficzny przykład, potrzebny niżej) Stworzenie obiektu range.

$^1$ Do tego przykładu wrócimy w dalszej części rozdziału.
$^2$ Przynajmniej na razie - patrz zastrzeżenie z poprzedniego rozdziału.

Nie wszystkie operacje są jednak elementarne: wiele operacji na wbudowanych obiektach Pythona, takich jak listy czy słowniki, wymaga czasu zależnego od aktualnego stanu (np. rozmiaru) tych obiektów.

Naszym pierwszym celem będzie demonstracja, jak ze złożoności fragmentów kodu wnioskować złożoność większego fragmentu. W przykładach poniżej, oraz w dalszej części rozdziału, nie odróżniamy symboli $i, j, n, \ldots$ od ich wersji monospace: i, j, n, ...

Przykład 1 (wstępny). Rozważmy następujący kod:

    def f(n):
        for i in range(n):
            for j in range(n):
                k = 2

Po wywołaniu f(n), "zewnętrzna" pętla wykonuje się $n$ razy (tworząc najpierw, jednorazowo, obiekt range). Za każdą jej iteracją wykonuje się pętla wewnętrzna. Zachowanie pętli "wewnętrznej" nie zależy od wartości i (czyli numeru iteracji pętli zewnętrznej). Pętla wewnętrzna, za każdym razem gdy zostaje osiągnięta, tworzy obiekt range i $n$ razy wykonuje przypisanie. W sumie zatem zostanie wykonanych $1 + n \cdot(1 + n) \in \Theta(n^2)$ operacji.

Przykład 1 (właściwy). Rozważmy następujący kod:

    def g(n):
        for i in range(n):
            for j in range(i):
                k = 2

Różnica względem poprzedniego przykładu jest w zasięgu wewnętrznej pętli. Liczba jej iteracji zależy teraz od i. Tak jak poprzednio, obiekt range tworzony jest na początku iteracji pętli zewnętrznej, i z każdym razem, gdy zaczyna wykonywać się pętla wewnętrzna. Liczba przypisań wykonanych w pętli wewnętrznej wynosi $i$ dla $i$-tej iteracji pętli zewnętrznej. W sumie wykonanych jest zatem $1 + n + 0 + 1 + \ldots + (n-1) = 1 + n + \frac{n(n-1)}{2} \in \Theta(n^2)$ operacji.
Możemy tę analizę wykonać trochę inaczej. Rozważmy czas działania wyłącznie pętli wewnętrznej:

    def g(n):
        for i in range(n):
            for j in range(i):
                k = 2
 Ten czas, asymptotycznie, jest oczywiście klasy $\Theta(i)$. Pokażemy teraz, że już z tej informacji o asymptotycznym czasie działania wewnętrznej pętli (w zależności od $i$) możemy wywnioskować czas działania pętli zewnętrznej (a zatem całej funkcji g). Używając wyłącznie wiedzy o asymptotycznym czasie działania pojedynczej iteracji zewnętrznej pętli, możemy zaprezentować g(n) jako:

    def g(n):
        for i in range(n):
            ... # Θ(i)
 gdzie ... reprezentuje operację lub ciąg operacji o czasie klasy $\Theta(i)$. Wobec tego, czas działania g(n) jest postaci (wliczając tworzenie obiektu range): $$1 + \sum_{i=0}^{n-1}T(i)$$ dla pewnej $T(i) \in \Theta(i)$. Możemy dobrać stałe $m, M > 0$ takie, że $m \cdot i \leq T(i) \leq M \cdot i$ (dla dostatecznie dużych $i$). Wtedy możemy oszacować sumaryczny czas działania g(n) jako: $$1 + m \cdot \sum_{i=0}^{n-1} i \leq 1 + \sum_{i=0}^{n-1}T(i) \leq 1 + M \cdot \sum_{i=0}^{n-1} i.$$ Lewym ograniczeniem jest $1+m \cdot \frac{n(n-1)}{2}$, a prawym $1+M \cdot \frac{n(n-1)}{2}$. Obie funkcje są klasy $\Theta(n^2)$, a więc takim jest również czas działania g(n).

Jeszcze prościej: wiedząc, że pojedyncza iteracja zewnętrznej pętli wyraża się funkcją klasy $\Theta(i)$, możemy bez straty ogólności założyć, że tą funkcją jest $T(i) = i$.

Przykład 2. Rozważmy następujący kod:

    def h(n):
        for i in range(n):
            if i % 2 == 0:
                k = 2
            else:
                k = 2
                l = 3
 Liczba operacji w kolejnych iteracjach pętli zależy od i. Potrafimy wprawdzie dokładnie rozstrzygnąć, ile ich będzie ($3$ dla liczb parzystych, $4$ dla nieparzystych), jednak możemy przyjąć, że przykład reprezentuje sytuację, gdzie takiego rozstrzygnięcia trudno dokonać. Zauważmy jednak, że liczba ta zawsze jest stała. Postępując jak w poprzednim przykładzie, prezentujemy h(n) jako:

    def h(n):
        for i in range(n):
            ... # Θ(1)
 a stąd już nietrudno wywnioskować, że czas działania h(n) jest klasy $\Theta(n)$.

Przykład 3. Rozważmy następujący kod:

    def inner(n):
        for i in range(n):
            k = 2

    def outer(n):
        for i in range(n):
            inner(i)
 Znanymi już metodami rozstrzygamy, że czas wykonania inner(n) jest klasy $\Theta(n)$. Zatem możemy przedstawić outer(n) jako:

    def outer(n):
        for i in range(n):
            ... # Θ(i)
 Wtedy identycznie jak w Przykładzie 1 (właściwym), czas działania outer(n) jest klasy $\Theta(n^2)$.

Przykład 4. Rozważmy następujący kod:

    def func(n):
        lst = list(range(n)) # Θ(n)
        while len(lst) > 0:
            lst.pop(0) # Θ(len(lst))
 W kodzie występują pewne operacje, które nie są elementarne (lub nie wiemy, że są elementarne). Są to:

  • Utworzenie listy długości $n$: czas klasy $\Theta(n)$.
  • Odczytanie długości listy: czas stały.
  • Usunięcie elementu o indeksie $0$ z listy długości $n$: czas $\Theta(n)$.

W dalszej części rozdziału wyjaśnimy, skąd brać informacje o powyższych czasach. Znając ich klasy, możemy wywnioskować czas działania func(n):

  1. Najpierw tworzona jest lista - $\Theta(n)$ operacji.
  2. Nastepnie w pętli z każdą iteracją sprawdzana jest długość listy (jedna operacja), porównywana z $0$ (jedna operacja), i usuwany jest element z początku listy w czasie $\Theta(i)$ (bez straty ogólności: dokładnie $i$ operacji), gdzie $i$ to długość malejącej listy: $i = n, n-1, n-2, \ldots, 1$. Stąd czas wykonania pętli jest klasy $$(2 + n) + (2 + n-1) + (2 + n - 2) + \ldots + 3 \in \Theta(n^2).$$ Ponieważ $\Theta(n^2) > \Theta(n)$, czas działania func(n) jest klasy $\Theta(n^2)$.

Złożoność operacji na kolekcjach Pythona

W ostatnim przykładzie poprzedniego podrozdziału pojawiły się operacje na listach, które nie wykonują się w czasie stałym. Wynika to z wewnętrznej implementacji klasy list. Wewnętrzną implementację list omówimy w następnym podrozdziale. Przyjrzymy się jednak czasom operacji na podstawowych typach danych Pythona (m.in. listach, słownikach, zbiorach) podanym w dokumentacji języka. Czasy te są podane na stronie https://wiki.python.org/moin/TimeComplexity i dotyczą "standardowej" implementacji Pythona. W tym podrozdziale krótko skomentujemy przedstawione na stronie dane.

Strona opisuje czasy działania operacji na czterech typach danych, z których na razie znamy list, set i dict. Każda tabelka zawiera dwie kolumny z czasami. Dla nas interesująca jest ta pierwsza, przedstawiająca średni czas danej operacji. Kolumna druga opisuje tak zwany zamortyzowany czas pesymistyczny, którego nie omówimy na wykładzie. W znacznej części przypadków, $O$ można zastąpić przez $\Theta$.

Zwrócimy teraz uwagę na niektóre z podanych czasów (rozmiarem danych jest rozmiar kolekcji, czyli np. długośc listy):

  • Kopiowanie (a także tworzenie nowych) kolekcji wykonuje się w czasie liniowym.
  • Odczytywanie obiektu spod danego indeksu na liście wykonuje się w czasie stałym. Podobnie dla odczytania wartości stowarzyszonej z kluczem w słowniku.
  • Zbadanie, czy element znajduje się na liście wykonuje się w czasie liniowym (!).
  • Zbadanie, czy znajduje się w zbiorze (lub jako klucz w słowniku) wykonuje się w czasie stałym.
  • Operacje mnogościowe na zbiorach wykonują się w czasie proporcjonalnym do rozmiarów zbiorów.
  • Dokładanie elementu na koniec listy (lub usuwanie go) wykonuje się w czasie stałym, lecz dokładanie go na początku lub w środku listy już nie.

Widzimy stąd, że (dostatecznie duże) zbiory sprawdzają się lepiej od list, gdy ważna jest dla nas operacja sprawdzania, czy element należy do kolekcji. To nie powinno zaskakiwać - zbiory są implementowane tak, aby dawać dobre gwarancje czasowe na tę podstawową operację teoriomnogościową.

Wewnętrzna implementacja list

W tym podrozdziale omówimy, w jaki sposób Python wewnętrznie reprezentuje instancje klasy list. W ten sposób zademonstrujemy konkretny sposób organizacji danych w pamięci, jednoczeście tłumacząc - dokładniej niż na stronie dokumentacji z poprzedniego podrozdziału - czasy działania operacji listowych.

Uwaga. W poniższym opisie będziemy stosowali pewne uproszczenia: nie podamy różnic między rodzajami adresów obiektów, oraz nie omówimy niuansów związanych z dodawaniem elementów na koniec listy, oraz związanym z tymi niuansami pojęciem zamortyzowanego czasu operacji. Ponadto, opis dotyczy "standardowej" implementacji Pythona (CPython).

Każdy obiekt w Pythonie zajmuje pewien obszar pamięci. Miejsce, w którym ten obszar się zaczyna nazwiemy jego adresem. Adres ten jest cztero- lub ośmiobajtową liczbą, którą możemy utożsamić z fizycznym miejscem w pamięci komputera. Znając adres obiektu, otrzymujemy natychmiastowy dostep do tego obiektu. Wewnętrznie, nazwy (zmienne) w Pythonie pamiętają takie właśnie adresy.

Obiekty typu list zajmują zatem pewien obszar pamięci. W tej pamięci zapisane są pewne dane dotyczące listy: jej aktualna długość, oraz pewne dodatkowe informacje potrzebne dla wewnętrznej "księgowości" Pythona (stąd: odczytanie długości listy wymaga tylko stałego czasu). Najważniejszą częścią listy jest jednak adres "właściwej" listy: ciągłego obszaru pamięci, w którym, w stałej odległości, ułożone są kolejne adresy obiektów umieszczonych na liście. Same obiekty nie leżą "na" liście (mogą przecież istnieć niezależnie od bycia elementem listy).

Reprezentacja przykładowej listy:


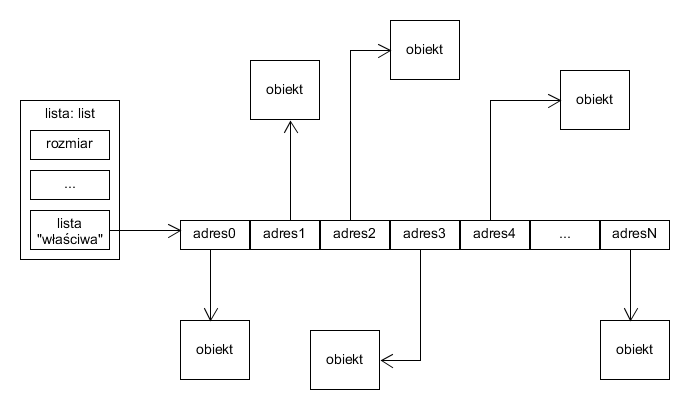
Przykładowa lista i obiekty na niej

Kolejne adresy na "właściwej" liście są ułożone zgodnie z ich indeksami na liście. Ponieważ zajmują stały rozmiar, znalezienie adresu obiektu spod danego indeksu wymaga stałej liczby operacji: mając listę (tzn. jej adres) oraz indeks, możemy odczytać adres listy "właściwej" i powiększyć go o indeks pomnożony przez rozmiar adresu, otrzymując miejsce, w którym znajduje się adres szukanego obiektu.

Operacji potrzebnych do odczytania adresu obiektu potrzeba zatem niewiele (w szczególności jest to czas stały, zgodnie z tabelką z poprzedniego podrozdziału).

Ułożenie adresów na liście "właściwej" zgodnie z ich indeksami jest jednak kluczowe. Własność ta musi zostać zachowana, gdy lista zostaje modyfikowana. Nie jest to problem, gdy element jest dokładany na koniec listy:


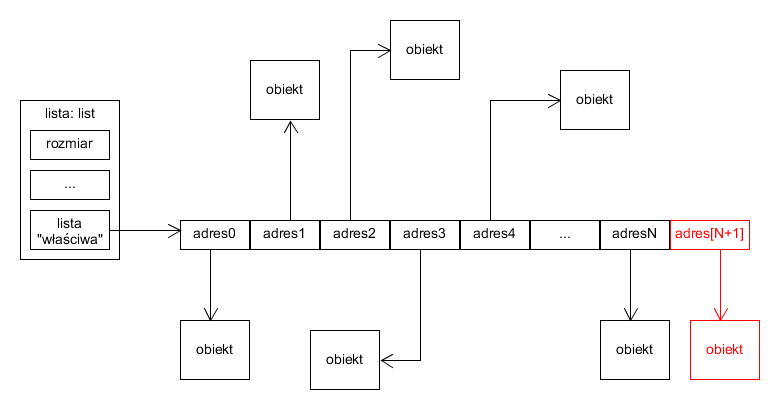
Przykładowa lista po dołożeniu elementu na jej koniec

Podobnie nie jest problemem usunięcie obiektu z końca listy. Problem pojawia się jednak, gdy element dodajemy pod istniejącym indeksem listy. Wtedy adresy obiektów o większych indeksach muszą zostać przesunięte o jedno miejsce w prawo, aby została zachowana zgodność kolejności:


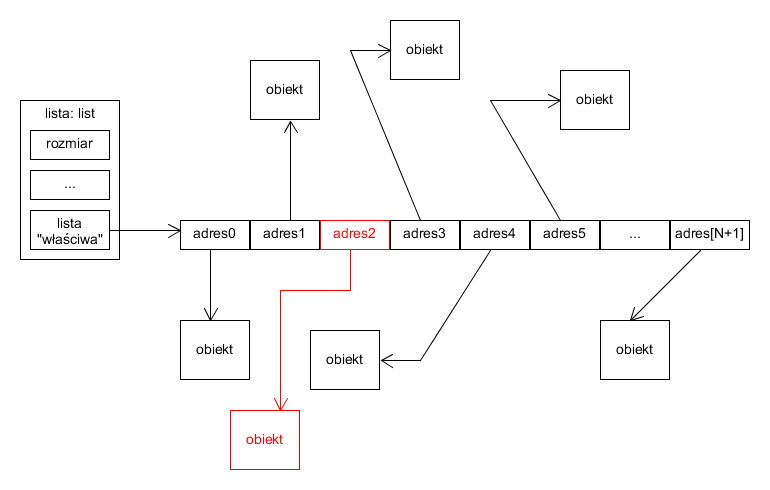
Przykładowa lista (pierwszy stan) po dołożeniu elementu pod indeksem 2.

Adresów, które musimy przesunąć jest tym więcej, im niższy indeks, pod który wstawiamy element. Czas operacji wstawiania jest zatem proporcjonalny do liczby elementów na liście na prawo od aktualnie wstawianego. W najgorszym wypadku, gdy wstawiamy element pod indeks $0$, wszystkie adresy muszą zostać przesunięte.

Analogiczna sytuacja zachodzi, gdy usuwamy element: odpowiednie adresy muszą zostać przesunięte w lewo, aby "załatać dziurę":


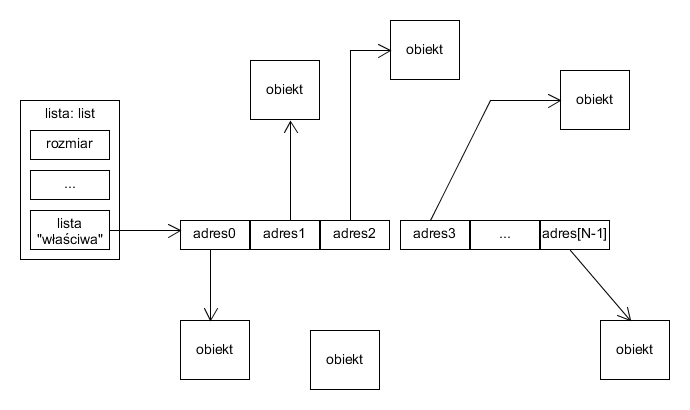
Przykładowa lista (pierwszy stan) po usunięciu elementu spod indeksu 3.

Tłumaczy to liniowość operacji usuwania/wstawiania "pośrednich" elementów na liście, zgodnie z tabelką czasów.

Eksperyment

Zarówno dokumentacja Pythona, jak i teoria wynikająca z poprzedniego rozdziału stanowią, że dla listy lst długości $n$, czas operacji lst.pop() jest klasy $\Theta(1)$, natomiast czas operacji lst.pop(0) jest klasy $\Theta(n)$. Rozważmy następujący kod:

def f(n):
    lst = list(range(n)) # Θ(n)
    while len(lst) > 0:
        lst.pop() # Θ(1)


def g(n):
    lst = list(range(n)) # Θ(n)
    while len(lst) > 0:
        lst.pop(0) # Θ(len(lst))

Obie funkcje tworzą listy długości $n$ (zakładamy tutaj, że dzieje się to w czasie liniowym!), a następnie usuwają z niej elementy - f kolejno z końca, g kolejno z początku. Analizując jak w przykładach z początku rozdziału, stwierdzamy, że funkcje f i g działają w czasach $\Theta(n)$ i $\Theta(n^2)$ odpowiednio. Czasy te możemy też zmierzyć eksperymentalnie.

Dla $n = 0, 1000, 2000, \ldots, 200000$, zmierzone czasy wykonania f(n) (w milisekundach, na średniej klasy sprzęcie) nanosimy na wykres (na niebiesko), zaznaczając też (na czerwono) funkcję liniową, która najlepiej (według tak zwanej metody najmniejszych kwadratów) przybliża uzyskane wyniki:

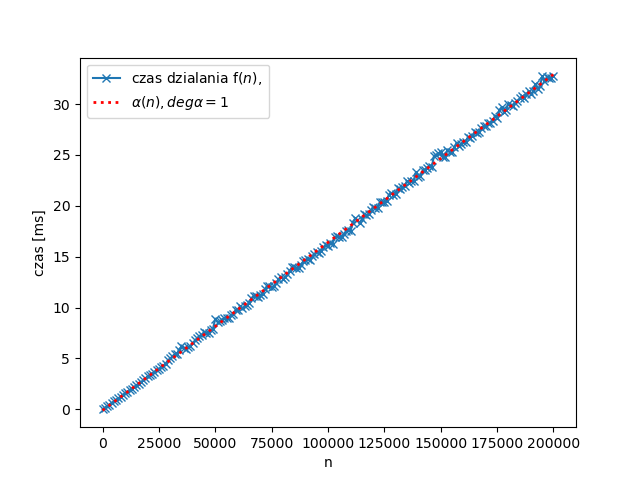
Podobnie dla g(n), tym razem dla $n = 0, 1000, 2000, \ldots, 50000$, gdzie wyniki przybliżamy nie funkcją liniową, a wielomianem drugiego stopnia:

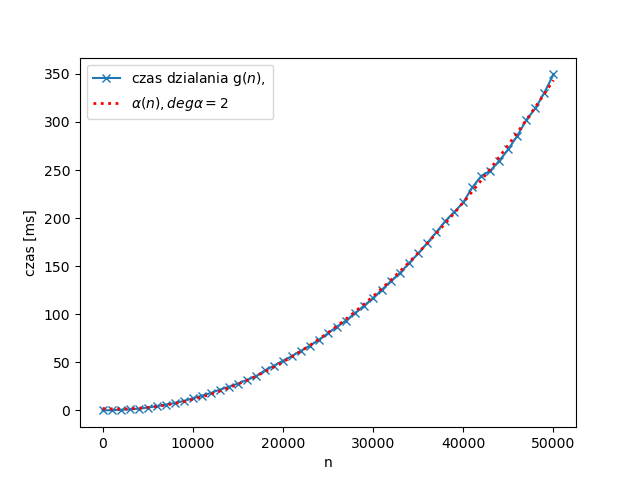
Uzyskane czasy są zatem zgodne z oczekiwaniami: w pierwszym przypadku rosną liniowo, w drugim kwadratowo.

Złożoność algorytmów - dodatkowe uwagi

W tym podrozdziale uzupełnimy pewne informacje dotyczące analizy asymptotycznej złożoności algorytmów oraz związane z nią konwencje.

Limitacje analizy złożoności

Przedstawiona na wykładzie analiza złożoności pozwala szacować czas wykonania algorytmów. Ma ona jednak pewne ograniczenia. Podamy dwa przykłady.

I. Paralelizacja. Współczesne komputery nawet przeciętnych konsumentów są wyposażone w wiele procesorów logicznych (rzeczywistych lub wirtualnych rdzeni). Jeszcze więcej procesorów mają superkomputery. Każdy taki procesor jest w stanie wykonywać instrukcje (w pewnym uproszczeniu) niezależnie od pozostałych. Niektóre algorytmy mogą to wykorzystywać: ich efektywne implementacje będą dzielić obliczenia pomiędzy wiele rdzeni, proporcjonalnie zmniejszając czas pracy. Nie dla wszystkich algorytmów jest to możliwe. Analiza złożoności przedstawiona na wykładzie bada jedynie sumaryczny czas potrzebny na wykonanie instrukcji, zaniedbując, czy da się ten czas rozłożyć na wiele rdzeni.

II. Stałe mają znaczenie. Rozważmy trzy algorytmy:

  • Algorytm A wykonujący dokładnie $n^2$ pewnych operacji.
  • Algorytm B wykonujący dokładnie $2n^2$ takich samych operacji.
  • Algorytm C wykonujący dokładnie $1000000n$ takich samych operacji.

Analiza asymptotyczna "ignoruje stałe", traktując je jako szczegóły implementacji. Przez to rozstrzygnie, że algorytmy A i B są "tak samo" dobre, podczas gdy C jest "lepszy" (dla dostatecznie dużych danych). Widzimy jednak, że:

  • Z samej natury algorytmów wynika, że implementacje A będą wydajniejsze, od implementacji B.
  • Implementacje C będą wydajniejsze od implementacji A tylko dla danych rozmiaru co najmniej $1000000$. Taki rozmiar danych może okazać się nierealistyczny i niespotykany w praktyce, czyniąc algorytm A praktycznie lepszym, choć asymptotycznie gorszym.

Ilustracją do ostatniego podpunktu są algorytmy mnożenia macierzy. W takich algorytmach kluczową operacją jest mnożenie współczynników. Mnożenie macierzy rozmiaru $n \times n$ w sposób "naiwny" wymaga $n^3$ takich operacji: należy wyznaczyć $n^2$ współczynników, a każdy z nich jest iloczynem skalarnym jednego wiersza i jednej kolumny macierzy, które mnożymy; do jego obliczenia potrzeba $n$ mnożeń współczynników (a oprócz tego, $n-1$ dodawań). Jest to więc algorytm klasy $\Theta(n^3)$.

Istnieją inne algorytmy mnożenia macierzy. Dla macierzy $2 \times 2$ istnieje trik, pozwalający na wyliczenie iloczynu z użyciem jedynie siedmiu mnożeń, zamiast ośmiu jak w algorytmie naiwnym. Trik ten uogólnia się do macierzy $n \times n$, prowadząc do algorytmu Strassena mnożenia macierzy w czasie klasy $\Theta(n^{\log 7}) \approx \Theta(n^{2.81})$. Znaleziono też dalsze, asymptotycznie wydajniejsze algorytmy. Poniżej krótkie zestawienie czasów działania:

  • Zwykły ("naiwny") algorytm: $\Theta(n^3)$,
  • Strassen (1969): $\Theta(n^{\log 7}) \approx \Theta(n^{2.81})$,
  • Coppersmith–Winograd (1990): $O(n^{2.375477})$,
  • Stothers (2010): $O(n^{2.374})$, Vassilevska (2011): $O(n^{2.3728642})$, Le Gall (2014): $O(n^{2.3728639})$.

Z asymptotycznego punktu widzenia, każdy algorytm jest usprawnieniem względem poprzedniego. Okazuje się jednak, że wszystkie (z wyjątkiem algorytmu Strassena) algorytmy działają lepiej od "naiwnego" dopiero dla macierzy astronomicznych rozmiarów (niekoniecznie do zrealizowania w znanym wszechświecie), co czyni je niepraktycznymi. Algorytm Strassena natomiast, w typowej implementacji, jest lepszy od naiwnego dla macierzy rozmiaru około $100 \times 100$. Takie macierze nie są wielkie i rutynowo pojawiają się w wielu obliczeniach.

Pewne konwencje

Z notacja asymptotyczną związane są pewne konwencje. Przypomnijmy, że klasy $\Theta(\cdot)$ etc. są pewnymi podzbiorami zbioru funkcji $\mathbb{R}_{\geq 0}^{\mathbb{N}}$. Dla funkcji $f, g \in \mathbb{R}_{\geq 0}^{\mathbb{N}}$, sens ma więc zapis $g \in \Theta(f)$ oraz $g(n) \in \Theta(f(n))$. Powszechnie stosowana jest jednak konwencja pisania znaku równości zamiast należenia: $g(n) = \Theta(f(n))$. Jest to drobne nadużycie notacji, spotykane powszechnie poza akademickimi źródłami.

Innym zwyczajem jest dość częste używanie $O$ w miejscu $\Theta$. Może to wynikać z ograniczeń typograficznych (na przykład w kodach źródłowych, jeśli $\Theta$ nie jest akceptowanym znakiem). Może być też częścią niepisanej konwencji, w której istotne jest podanie tylko górnego ograniczenia wzrostu funkcji (przyjmując, że dolne ograniczenie jest mniej ważne, lub takie samo). Czasem wynika też z nieścisłego lub błędnego wręcz stosowania notacji.