G. Jagiella | ostatnia modyfikacja: 23.05.2024 |
Rozważmy następujący, klasyczny problem.
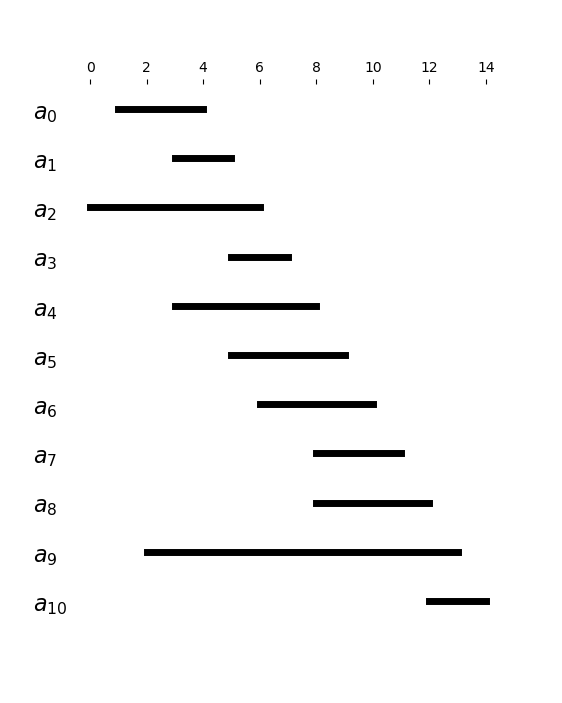
W problemie wyboru zajęć, mamy daną kolekcję $S = \{a_0, a_1, \ldots, a_{n-1}\}$ złożoną z $n$ otwartych odcinków. Oznaczmy $a_i = (s_i, f_i)$. Naszym zadaniem jest znalezienie największego możliwego podzbioru $S' \subseteq S$ składającego się z odcinków parami rozłącznych. Przez największy podzbiór mamy na myśli jego moc: nie interesuje nas sumaryczna długość odcinków.
Nazwa problemu wskazuje na jego naturalną interpretację, w której odcinki reprezentują zajęcia, a końce odcinków reprezentują czas rozpoczęcia i zakończenia zajęć. Problem rozumiemy wtedy jako wybór maksymalnej ilości zajęć, które ze sobą parami nie kolidują (tzn. są ze sobą kompatybilne). Przyjmujemy przy tym, że jeśli pewne zajęcia zaczynają się dokładnie w momencie, gdy inne się kończą, to są para zajęć kompatybilnych (co odpowiada założeniu otwartości odcinków).
W dalszej części rozdziału, będziemy używać terminologii z tej interpretacji (zajęcia, czasy rozpoczęcia i zakończenia, kompatybilność).
Problem jest natury optymalizacyjnej. Stosujemy więc standardową dla takich problemów terminologię. Przy oznaczeniach, jak wyżej, dowolny podzbiór $S' \subseteq S$ składający się z parami kompatybilnych zajęć nazwiemy rozwiązaniem dopuszczalnym. Rozwiązanie dopuszczalne o największej możliwej mocy nazwiemy rozwiązaniem optymalnym.
Będziemy zakładać, że zajęcia są uporządkowane względem czasu zakończenia $f_i$. W dalszej części rozdziału, będziemy posługiwać się następującymi przykładowymi danymi:
| $i$ | $0$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $s_i$ | $1$ | $3$ | $0$ | $5$ | $3$ | $5$ | $6$ | $8$ | $8$ | $2$ | $12$ |
| $f_i$ | $4$ | $5$ | $6$ | $7$ | $8$ | $9$ | $10$ | $11$ | $12$ | $13$ | $14$ |

W przykładzie, optymalnym rozwiązaniem (nie jedynym) jest zbiór $\{a_0, a_3, a_7, a_{10}\}$.
Najpierw spróbujemy rozwiązać ten problem z użyciem programowania dynamicznego - potem sprawdzimy, że istnieje prostsze rozwiązanie, naprowadzające na inną technikę projektownia algorytmów.
Określamy podproblemy: dla $i \in \{0, 1, \ldots, n\}$ oraz $t \in \{f_0, f_1, \ldots\, f_n\} \cup \{-\infty\}$, niech $P(i, t)$ oznacza (pod)problem optymalnego zajęć spośród tych o indeksie co najmniej $i$, których czas rozpoczęcia to co najmniej $t$ (czyli leżących na (pół)prostej $(t, \infty)$). Wtedy w szczególności:
Dla $P(i, t)$ definiujemy rozwiązania dopuszczalne i optymalne analogicznie, jak dla całego problemu.
Ustalmy $i < n$ oraz $t$ i rozważmy konstrukcję optymalnego rozwiązania $P(i, t)$. Rozważmy zajęcia $a_i = (s_i, f_i)$.
Powyższe w standardowy sposób narzuca nam zależności rekurencyjne między funkcją wartości rozwiązania $V(i, t)$, zdefiniowanej jako ilość zajęć w optymalnym rozwiązaniu $P(i, t)$. Dla wszystkich $t$:
Problem ma zatem własność optymalnej podstruktury. Wyróżnionych w nim podproblemów jest $\Theta(n^2)$, zatem rozwiązanie można wyznaczyć dynamicznie metodą "wstępną" w takim właśnie czasie. Istnieje jednak prostszy sposób.
W przypadku problemu $P(i, t)$, gdy $s_i \geq t$, mamy dwie opcje: albo dokładamy zajęcia $a_i$ do rozwiązania, zwiększając uzyskany zbiór zajęć o $1$ i redukując problem do $P(i+1, f_i)$; albo nie, redukując jedynie problem do $P(i+1, t)$. Jak się okaże, potrafimy zawczasu rozstrzygnąć, który z tych wyborów jest lepszy. Posłużymy się przykładem, na którym zbudujemy intuicję. Rozważmy problem $P(5, 5) = P(5, f_1)$ dla danych z przykładu z początku rozdziału. Mamy w nim dostępne zajęcia oznaczone na zielono, szukamy optymalnego wyboru zajęć zawartych w półprostej $(5, \infty)$:
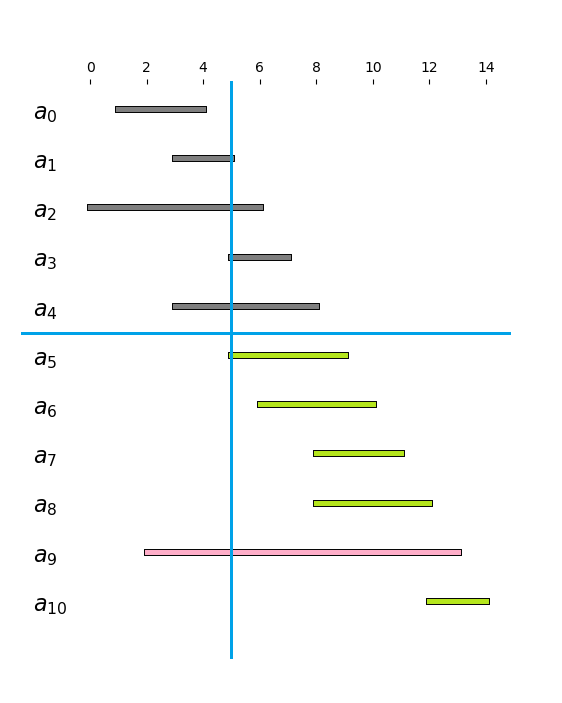
Intuicja mówi, że wybór $a_5$ jest optymalny: po pierwsze, powiększa on zbiór rozwiązań o $1$. Po drugie - ze względu na fakt, że zajęcia są uporządkowane względem czasów zakończenia - półprosta, w której mamy znaleźć jak najwięcej z pozostałych zielonych odcinków zmniejsza się najmniej, jak tylko to możliwe. Sformalizujmy tę obserwację w sposób ogólny.
Stwierdzenie. Załóżmy, że dla pewnego $P(i, t)$ zachodzi $t \leq s_i$. Wtedy istnieje optymalne rozwiązanie $P(i, t)$, w którym pierwsze zajęcia to $a_i = (s_i, f_i)$.
Dowód. Weźmy dowolne, optymalne rozwiązanie $S'$ problemu $P(i, t)$. Jest ono niepuste, ponieważ $\{a_i\}$ jest rozwiązaniem dopuszczalnym. Niech $a_k = (s_k, f_k)$ to pierwsze zajęcia w $S'$ (to znaczy: o najmniejszym czasie zakończenia). Mamy $f_i \leq f_k$, zatem zajęcia $a_i$ są kompatybilne ze wszystkimi zajęciami z $S'$ innymi, niż $a_k$. Możemy zatem zastąpić w $S'$ zajęcia $a_k$ przez $a_i$. Wtedy $S'' = (S \setminus \{a_k\}) \cup \{a_i\}$ jest rozwiązaniem $P(i,t)$ dopuszczalnym tej samej mocy, co $S'$, a zatem rozwiązaniem optymalnym.
Stwierdzenie pokazuje zatem, że w podanej sytuacji, wybór $a_i$ zawsze prowadzi do zbudowania części rozwiązania optymalnego. Rozwiązując $P(i, t)$, możemy działać następującą metodą "zstępną": jeśli $t \leq s_i$, dodajemy $a_i$ jako część rozwiązania i przechodzimy do rozwiązywania wynikłego podproblemu $P(i + 1, f_i)$. W przeciwnym wypadku rozwiązujemy $P(i+1, t)$. Powtarzamy aż do osiągnięcia problemu trywialnego (postaci $P(n, -)$). W każdej z sytuacji, wybór jest zdeterminowany prawdziwością $t \leq s_i$. W szczególności, jeśli zachodzi $t \leq s_i$, to w ogóle nie zachodzi potrzeba badania podproblemu $P(i+1, t)$, ani kolejnych jego podproblemów, jak ma to miejsce w rozwiązaniu metodą "wstępną".
Kroki optymalnego wyboru zajęć ($(s_i, f_i)$ - ciąg zajęć, uporządkowany niemalejąco przez $f_i$).
- Przypisz $t = -\infty$.
- Dla kolejnych zajęć $i = 0, 1, \ldots, n - 1$:
2a. Jeśli $s_i < t$, kontynuuj.
2b. Jeśli $s_i \geq t$, oznacz $a_i$ jako część rozwiązania i przypisz $t = f_i$.
Stąd przykładowa implementacja:
from math import inf
def most_tasks(tasks):
# Poniższą linijkę możemy odkomentować, jeśli nie zakładamy, że tasks jest posortowane czasami zakończeń:
# tasks = sorted(tasks, key=lambda t: t[1])
t = -inf
tasks_taken = []
for i, task in enumerate(tasks):
start, end = task
if start >= t:
tasks_taken.append(i)
t = end
return tasks_taken
task_list = [(1, 4), (3, 5), (0, 6), (5, 7), (3, 8), (5, 9),
(6, 10), (8, 11), (8, 12), (2, 13), (12, 14)]
print(most_tasks(task_list))
[0, 3, 7, 10]
Podane przez algorytm rozwiązanie jest identyczne z podanym pod przykładem.
W kolejnych iteracjach pętli dokonujemy wyboru związanego z podproblem postaci $P(i, -)$ dla kolejnych $i$. Złożoność czasowa tego algorytmu to zatem $\Theta(n)$ (lub $O(n \log n)$ w wersji z sortowaniem). Jego złożonośc pamięciowa to $O(n)$ - rozmiar tasks_taken, czyli rozwiązania.
Rozwiązanie problemu wyboru zajęć sprawadziło się do sekwencji wyborów, w którym każdy został dokonany tak, aby był lokalnie optymalny - czyli zwiększał częściowo utworzone rozwiązanie o pojedyncze zajęcia, jeśli tylko było to możliwe. Algorytmy polegające na kolejnym dokonywaniu takich lokalnie optymalnych ("zachłannych") wyborów, sprowadzających problemy do mniejszych podproblemów (wynikłych z dokonanego wyboru), nazywają się algorytmami zachłannymi.
Aby problem poddawał się algorytmowi zachłannemu, oprócz własności optymalnej podstruktury (pozwalającej na konstrukcję optymalnego rozwiązania problemu z rozwiązań podproblemu, jak w programowaniu dynamicznym), musi mieć też własność zachłannego wyboru - czyli własność gwarantującą, że lokalnie optymalne wybory rzeczywiście prowadzą do optymalnych globalnych rozwiązań.
Nie wymagamy natomiast, aby wyróżnionych podproblemów było stosunkowo mało (własność wspólnych podproblemów), gdyż rozwiązanie zachłanne pozwala nam z reguły na znaczne ograniczenie ilości podproblemów, które musimy rozwiązać. To typowo skutkuje mniejszą złożonością (czasową i pamięciową) względem rozwiązań dynamicznych.
Problemy przedstawione w rozdziałach o programowaniu dynamicznym nie mają własności zachłannego wyboru (poza ich szczególnymi przypadkami). Poniżej przedstawimy kilka problemów, które ją mają:
Ciągły problem plecakowy. Problem jest zbliżony do dyskretnego problemu plecakowego, ale zakładamy, że w plecaku można umieszczać dowolne ułamkowe części przedmiotu (ułamek przedmiotu ma proporcjonalnie mniejszą wartość). O przedmiotach można zatem myśleć jako np. cieczach o pewnej wartości w przeliczeniu na kilogram lub litr. Optymalną strategią wypełniania plecaka jest umieszczanie w nim przedmiotów (lub ich ułamków) o jak największej wartości w przeliczeniu na wagę, aż do wyczerpania pojemności plecaka lub przedmiotów o wartości dodatniej.
Problem wydawania reszty. Zadaniem jest wydanie podanej reszty monetami o nominałach 1zł, 50gr, 20gr, 10gr, 5gr, 2gr i 1gr, używając jak najmniejszej ilości monet. Optymalną strategią jest wydawanie reszty używając monet o jak największym dostępnym nominale, aż do wydania całej reszty. Przykładowo: 1,68zł wydajemy jako 1zł + 50gr + 10gr + 5gr + 2gr + 1gr. Uwaga: ta strategia nie działa dla dowolnych nominałów. Przykładowo, dla nominałów 1, 5 i 6, strategia zachłanna nakazuje wydać 10 jako 6+1+1+1+1, jednak optymalnym rozwiązaniem jest użycie dwóch monet o nominale 5.
Znany już algorytm Prima budowania minimalnego drzewa rozpinającego w grafie skierowanym ważonym. Drzewo budujemy w nim poczynając od wybranego wierzchołka, powiększając je w każdym kroku o nową krawędź i wierzchołek tak, aby waga dodanej krawędzi była najmniejsza możliwa.
Lista problemów, poddających się technice zachłannej, jest oczywiście znacznie bogatsza.
Podsumujmy dział diagramem częściowo opisującym taksonomię algorytmów stosowanych do problemów, których rozwiązania sprowadzają się do rozwiązań podproblemów:
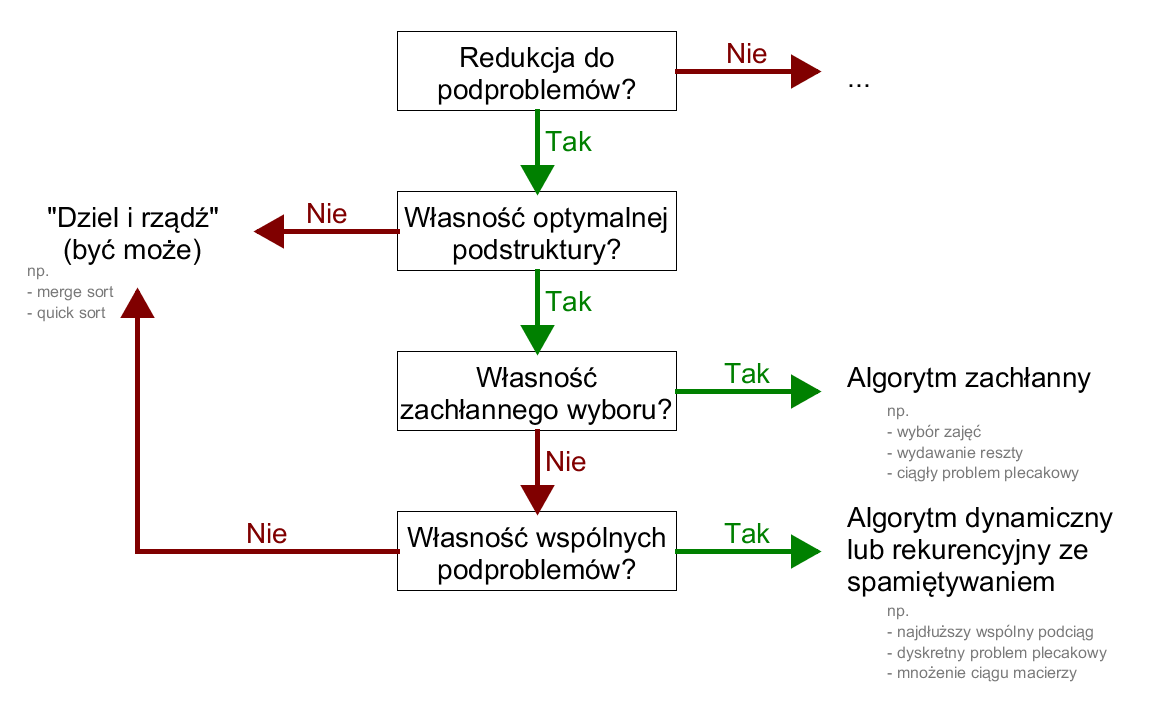
Diagram nie jest wyczerpujący - pokazuje jedynie niektóre z dostępnych technik programowania. Jest to jednak szeroki fragment - programowanie dynamiczne, zachłanne i metoda "dziel i rządź" to szeroko stosowane, fundamentalne metody projektowania algorytmów.
Zwracamy uwagę, że diagram sugeruje, że w sytuacji problemów, wykazujących własność optymalnej podstruktury oraz zarówno własność wspólnych podproblemów jak i własność zachłannego wyboru (a więc takich, dla których istnieją algorytmy dynamiczne i algorytmy zachłanne - na przykład problem wyboru zajęć), preferujemy rozwiązane zachłanne. Jest to dobra reguła: algorytmy zachłanne zazwyczaj znacznie redukują ilość podproblemów, które musimy rozwiązać, prowadząc do lepszych złożoności.
Uzupełnimy kwestię, która pojawiła się już przy niektórych rozważaniach na wykładzie: złożoność czasowa operacji na liczbach całkowitych. Złożoności algorytmów opisywaliśmy często jako ilość operacji na liczbach (np. mnożeń skalarnych). Przyjmowaliśmy zazwyczaj, że pojedyncza operacja jest wykonywana w czasie stałym. W tym podrozdziale pokażemy, kiedy to założenie jest uprawnione.
Rozważmy algorytmy ręcznego dodawania i mnożenia liczb całkowitych (dla uproszczenia: naturalnych), czyli dodawanie i mnożenie w słupku. Policzmy, ile operacji na poszczególnych cyfrach zapisu dziesiętnego musimy wykonać. Dla liczb o $n$ i $m$ cyfrach, dodawanie wymaga $\Theta\big(\max(n,m)\big)$, a mnożenie $\Theta(nm)$ takich operacji.
Tutaj złożoność wyraziliśmy w zależności od ilości cyfr liczby. Ponieważ do zapisu dziesiętnego liczby $N$ potrzebujemy (w zaokrągleniu) $\log_{10}N$ cyfr, złożoność możemy też wyrazić w zależności od samej liczby. Dla liczb $N$ i $M$ zatem, dodawanie i mnożenie wymagają $\Theta\big(\max(\log_{10} N, \log_{10} M)\big)$ i $\Theta(\log_{10} N \cdot \log_{10} M)$ operacji odpowiednio. Ponieważ logarytmy o podstawach $2$ i $10$ różnią się jedynie stałym czynnikiem, mamy $$ \begin{align*} \Theta\big(\max(\log_{10} N, \log_{10} M)\big) & = \Theta\big(\max(\log N, \log M)\big),\\ \Theta(\log_{10} N \cdot \log_{10} M) & = \Theta(\log N \cdot \log M). \end{align*} $$
Przyjmując też, że $N$ i $M$ mają tyle samo cyfr, otrzymujemy odpowiednie złożoności $\Theta(\log N)$ i $\Theta(\log^2 N)$.
Odniesiemy powyższe obserwacje do arytmetyki cyfrowej.
Jedną z podstawowych jednostek danych, na których wewnętrznie operują procesory, jest tak zwane słowo maszynowe. Słowo to składa się z pewnej ustalonej ilości bitów - cyfr dwójkowych. Ilość ta (długość słowa) zależy od procesora i jego architektury, współcześnie jest to zazwyczaj $64$, i taką wartość dla uproszczenia przyjmiemy dalej. Podstawowym sposobem interpretacji słowa maszynowego jest liczba naturalna, zapisana z użyciem $64$ cyfr, z których część może być wiodącymi zerami. Tak utworzoną liczbę nazwiemy liczbą $64$-bitową. Może ona przyjmować wartości naturalne z przedziału $[0, 2^{64})$. Procesory potrafią w natywny sposób wykonywać, w stałym czasie, podstawowe operacje arytmetyczne na takich $64$-bitowych liczbach (znów, dla uproszczenia: ograniczamy się do dodawania i mnożenia).
Zwróćmy uwagę, że powyższy wynik mnożenia ma naturalną interpretację. W systemie pozycyjnym o podstawie $2^{64}$, liczba $64$-bitowa to po prostu pojedyncza cyfra. Iloczyn dwóch jednocyfrowych liczb $A$ i $B$ jest (co najwyżej) dwucyfrową liczbą składającą się z cyfr $C$ i $D$, gdzie $D$ to cyfra jedności, a $C$ to cyfra $2^{64}$-rek. Podobnie dla dodawania: suma dwóch jednocyfrowych liczb to liczba (co najwyżej) dwucyfrowa, z których cyfra $2^{64}$-rek to $0$ lub $1$.
Różne systemy arytmetyczne - w tym implementacja typu całkowitoliczbowego int w Pythonie - reprezentują liczby większe, niż $2^{64}-1$ (tak zwane bignumy - big numbers) zgodnie z powyższą interpretacją. Duża liczba $N$ jest reprezentowana jako skończony ciąg (lista) liczb $64$-bitowych, które reprezentują kolejne cyfry $N$ w zapisie w systemie o podstawie $2^{64}$. Ciąg $(a_2, a_1, a_0)$ oznacza zatem liczbę $a_2 \cdot 2^{128} + a_1 \cdot 2^{64} + a_0$.
Operacje dodawania i mnożenia takich dużych liczb można więc zaimplementować jako operacje "w słupku", sprowadzając je do działania na pojedynczych cyfrach, które procesor wykonuje natywnie w czasie stałym. Analiza złożoności takich algorytmów jest tu identyczna, jak dla działań w systemie dziesiętnym z początku rozdziału. Stąd:
Fakt. Operacja $N + M$ ma złożoność czasową $\Theta\big(\max(\log N, \log M)\big)$. Operacja $N \cdot M$ ma złożoność $\Theta(\log N \cdot \log M)$.
Gdy liczby są dostatecznie małe (na przykład są rozmiaru jednego słowa maszynowego), można przyjąć, że operacje są stałe. Gdy jednak operujemy na bardzo dużych liczbach, czas działań należy uwzględniać w opisie złożoności czasowej algorytmów, a ich rozmiar w złożoności pamięciowej.
Często nietrywialny koszt działań arytmetycznych na obiektach (niekoniecznie liczbach - przykładowo, na macierzach) skłania nas do szukania optymalnego sposobu wykonywania działań, aby wynik uzyskać jak najmniejszą pracą. Przykładem tej sytuacji było optymalne nawiasowanie iloczynu macierzy z poprzedniego rozdziału. W tym podrozdziale omówimy sposób szybkiego potęgowania.
Niech $(A, \circ)$ będzie zbiorem zamkniętym na działanie $\circ$. O działaniu zakładamy, że jest łączne. Dla uproszczenia załóżmy też, że ma element neutralny $1 \in A$. Intuicyjnie, o $\circ$ można myśleć jako o działaniu grupowym (np. złożenie permutacji w grupie $S_n$) lub mnożeniu w pewnym pierścieniu (np. mnożenie macierzy w $M_{n \times n}(\mathbb{R})$, lub zwykłe mnożenie w ciele liczb rzeczywistych). Zdefiniujmy potęgowanie w sensie działania $\circ$ w następujący sposób. Niech $a \in A$ i $n \in \mathbb{N}$. Wtedy: $$ a^n = \underbrace{a \circ a \circ \ldots \circ a}_{n\text{ razy}}, $$ przyjmując też $a^0 = 1$. Zwróćmy uwagę, że definicja ma sens dzięki założeniu łączności. Jeśli $\circ$ interpretujemy jako mnożenie, potęgowanie w sensie $\circ$ to zwykłe potęgowanie. W dalszej części podrozdziału, operację $\circ$ będziemy nazywać mnożeniem.
Rozważmy teraz sytuację, w której mamy typ danych reprezentujący elementy $A$ wraz z "mnożeniem" $\circ$ i chcemy zaiplementować operację potęgowania w sensie $\circ$. Podnosząc $a$ do potęgi $n$, mamy naturalny, "naiwny" sposób, polegający na wyliczaniu kolejnych potęg przez domnażanie wyniku przez $a$: $1, a, a^2, a^3, \ldots, a^n$. Implementując ten algorytm dla liczb typu int (zaniedbując fakt, że mamy już w Pythonie wbudowaną operację potęgowania tych liczb), otrzymujemy:
# powolne potęgowanie naiwne
def slowpow(a, n):
r = 1
for i in range(n):
r *= a
return r
print(slowpow(2, 8))
256
Implementację można łatwo zaadaptować dla typów innych, niż liczbowe. Algorytm ten wymaga $\Theta(n)$ mnożeń. Jego potencjalną zaletą jest, że oprócz wyliczania $a^n$ wylicza on też wszystkie potęgi $a$ o mniejszym wykładniku. Często jednak interesuje nas wyznaczenie konkretnej, być może bardzo dużej potęgi $a$. Sytuacja taka ma miejsce np. w kryptografii, gdzie wyznaczamy dużą potęgę pewnej liczby, modulo pewna liczba $m$. Ze względu na to, że wszystkie operacje wykonują się modulo $m$, pracujemy na liczbach ograniczonych rozmiarów (a więc, zgodnie z poprzednim podrozdziałem, operacje mnożenia można traktować jako stałe).
Poczyńmy obserwację, że jeśli wykładnik $n$ jest potęgą dwójki, wówczas łatwo jest wyznaczyć wartość $a^n$ używając niewielu mnożeń. Dla dowolnego $k$, mając znaną wartość $a^k$, wartość $a^{2k}$ możemy wyznaczyć podnosząc $a^k$ do kwadratu (wykonując pojedyncze mnożenie). Możemy zatem skonstruować ciąg, zaczynający się od $a$, którego każdy element jest kwadratem poprzedniego: $a, a^2, a^4, \ldots, a^{2^m}, a^{2^{m+1}}, \ldots$. Otrzymanie $a^{2^m}$ wymaga więc $\Theta(m)$ mnożeń. Przyjmując wykładnik $n = 2^m$ oznacza to, że koszt wyliczenia $a^n$ to zaledwie $\Theta(\log n)$ mnożeń.
Powyższy sposób można łatwo uogólnić dla dowolnego $n \in \mathbb{N}$. Badając zapis wykładnika $n$ w systemie dwójkowym, możemy znaleźć jego jednoznaczne przedstawienie jako sumę (różnych) potęg dwójki: $n = 2^{i_0} + 2^{i_1} + \ldots + 2^{i_k}$ dla pewnych naturalnych $i_0 < i_1 < \ldots < i_k$. Koniecznie $2^{i_k} \leq n$, czyli $i_k \leq \log n$, a w konsekwencji $k \leq \log (n)$. Mamy zatem: $$a^n = a^{2^{i_0} + 2^{i_1} + \ldots + 2^{i_k}} = a^{2^{i_0}} \circ a^{2^{i_1}} \circ \ldots \circ a^{2^{i_k}}.$$
Znalezienie wartości (wszystkich) czynników $a^{2^{i_j}}$ dla $j = 0, \ldots, k$ wymaga $\Theta(k)$ mnożeń, a wymnożenie ich wszystkich $\Theta(k)$, w sumie zatem $\Theta(k)$ operacji. Wyznaczanie tego iloczynu możemy zalgorytmizować (poniżej, $r$ reprezentuje częściowo wyliczony wynik - iloczyn):
Kroki szybkiego potęgowania (wejście: $a$ - obiekt, $n$ - potęga).
- Niech $r = 1, b = a$.
- Dla $i = 0, 1, 2, \ldots, n$, dopóki $2^i < n$:
2a. Jeśli $2^i$ pojawia się w rozkładzie $n$ na sumy potęg dwójki, domnóż $r$ przez $b$.
2b. Podnieś $b$ do kwadratu.
Niezmiennikiem iteracji jest zależność $b = a^{2^i}$ na początku pętli.
Przykład: niech $n = 200 = 128 + 64 + 8$. Śledzimy kolejne obroty pętli, zaczynając od $r = 1, b = 1, i = 0$.
- $b = a$; $2^i = 1$ nie pojawia się w rozkładzie, $r = 1$.
- $b = a^2$; $2^i = 2$ nie pojawia się w rozkładzie, $r = 1$.
- $b = a^4$; $2^i = 4$ nie pojawia się w rozkładzie, $r = 1$.
- $b = a^8$; $2^i = 8$ pojawia się w rozkładzie, $r = a^8$.
- $b = a^{16}$; $2^i = 16$ nie pojawia się w rozkładzie, $r = a^8$.
- $b = a^{32}$; $2^i = 32$ nie pojawia się w rozkładzie, $r = a^8$.
- $b = a^{64}$; $2^i = 64$ pojawia się w rozkładzie, $r = a^{72}$.
- $b = a^{128}$; $2^i = 128$ pojawia się w rozkładzie, $r = a^{200}$.
Powyższy algorytm ma złożoność $\Theta(\log n)$. W jego poniższej implementacji, rozstrzygnięcie, czy $r$ powinno zostać pomnożone przez odpowiednią potęgę $a$ zostaje rozstrzygnięte przez zbadanie odpowiadającej cyfry zapisu dwójkowego $n$. Cyfry te odczytujemy przez kolejne dzielenie $n$ przez $2$ (usuwając najmniejszą cyfrę) i sprawdzanie jej resztę z dzielenia przez $2$:
# potęgowanie szybkie
def fastpow(a, n):
r = 1
while n > 0:
if n % 2 == 1:
r *= a
a *= a
n //= 2
return r
print(fastpow(2, 8))
256