G. Jagiella

Skrypt do wykładu Programowanie 2 (Python)

ostatnia modyfikacja: 30.05.2020

Wykład 12 - programowanie dynamiczne, cz. 2

Spis treści

• Dyskretny problem plecakowy
  • Opis problemu
  • Rozwiązanie w sposób dynamiczny
• Interludium
• Optymalne mnożenie ciągu macierzy
  • Opis problemu
  • Rozwiązanie w sposób dynamiczny
• Dyskretny problem plecakowy - wersja minimum

Dyskretny problem plecakowy

Opis problemu

Dyskretny problem plecakowy (discrete knapsack problem, a także zero-jedynkowy problem plecakowy) to klasyczny problem z równie klasyczną narracją.

Załóżmy, że jesteśmy złodziejem pragnącym obrabować bogaty (mamy nadzieję) dom. Mamy ze sobą plecak o ograniczonej pojemności (wyrażonej w pewnych jednostkach, np. w kilogramach lub w litrach). W plecaku możemy wynieść znalezione w domu przedmioty. Każdy przedmiot wypełnia pewną część pojemności plecaka i ma znaną nam wartość u pasera. Naszym celem jest wyniesienie przedmiotów o jak największej sumarycznej wartości, nie przekraczając dostępnej pojemności plecaka.

Problem plecakowy (i jego warianty) pojawia się często w kontekście optymalnego zarządzania zasobami, na przykład optymalnego inwestowania kapitału.

Przykładowo, załóżmy, że mamy plecak o pojemności 15 kilogramów, oraz następujące przedmioty:

Przedmiot	Waga [kgf]	Wartość [zł]
Lampa stołowa	2	40
Wprowadzenie do algorytmów, T. Cormen i inni	2	160
Duży blender	3	70
Koń na biegunach	15	300
Kilogram tytanu	1	70
Dziwna ozdoba	4	25
Połamane krzesło	5	25
Półzabytkowy odkurzacz	6	180

Jak się przekonamy, optymalnym wyborem w tej sytuacji są: lampa, podręcznik Cormena, blender, kilogram tytanu i odkurzacz o łącznej wartości 520 zł i łącznej wadze 14 kilogramów.

Wyboru takiego chcielibyśmy oczywiście dokonać w sposób algorytmiczny. W tym celu, najpierw sprecyzujemy problem.

Danymi w dyskretnym problemie plecakowym są:

• Pojemność plecaka $W \in \mathbb{N}$.
• Kolekcję $n$ przedmiotów, indeksowanych przez $i = 0, 1, \ldots, n-1$.
• Ciąg liczb naturalnych $w_0, w_1, \ldots, w_{n-1}$, oznaczających wagi kolejnych przedmiotów.
• Ciąg liczb rzeczywistych $v_0, v_1, \ldots, v_{n-1}$, oznaczających wartości kolejnych przedmiotów.

Celem jest wybranie pewnej ilości przedmiotów, czyli podzbioru indeksów $J \subseteq \{0, 1, \ldots, n - 1\}$ tak, aby:

1. $\sum_{j \in J} w_j \leq W$,
2. $\sum_{j \in J} v_j$ było możliwie największe.

Zbiór indeksów $J$ spełniający warunek 1. będziemy nazywać rozwiązaniem dopuszczalnym. Każde rozwiązanie dopuszczalne spełniające warunek 2. nazwiemy rozwiązaniem optymalnym. Sumę $\sum_{j \in J} v_j$ nazwiemy wartością rozwiązania.

Zwracamy uwagę, że zarówno pojemność plecaka, jak i wagi przedmiotów są liczbami naturalnymi. Każdy przedmiot może zostać umieszczony w plecaku w całości lub wcale. Słowo "dyskretny" odnosi się do tej zero-jedynkowej natury problemu. Plecak nie musi zostać wypełniony w całości.

Poczyńmy tu pierwsze obserwacje dotyczące rozwiązania problemu. Po pierwsze, problem nie jest trywialny: naiwna strategia polegająca na wybieraniu przedmiotów najdroższych, lub takich, które mają największą wartość w przeliczeniu na kilogram, zawiodą. Przykładowo: mając dostępny plecak o pojemności 4 kg oraz przedmioty o wagach kolejno: 3, 2, 2 oraz odpowiadających wartościach 70, 40 i 40; optymalnym pakowaniem jest wzięcie obu przedmiotów o wadze 2 kg, mimo, że są warte mniej, niż ten pozostały (również w sensie ceny na wartości podzielonej przez wagę).

Siłowe rozwiązanie problemu, polegające na zbadaniu wszystkich możliwych podzbiorów przedmiotów i wybraniu najlepszego również nas nie satysfakcjonuje: taki algorytm ma złożoność co najmniej taką, jak ilość tych podzbiorów, czyli $\Omega(2^n)$.

Rozwiązanie w sposób dynamiczny

Zastosujmy (w świadomy sposób) technikę programowania dynamicznego do rozwiązania dyskretnego problemu plecakowego. Stosujemy oznaczenia takie, jak w opisie problemu w poprzednim podrozdziale.

Optymalna podstruktura i funkcja zysku. Najpierw opisujemy podproblemy, do rozwiązania których sprowadzamy rozwiązanie całego problemu. Pokazujemy, że znajdowanie ich optymalnych rozwiązań sprowadza się do szukania optymalnych rozwiązań stosownych podproblemów. Opiszemy też rekurencyjne zależności między funkcjami zysku (wartością rozwiązania).

Dla $i = 0, 1, \ldots, n$ oraz $w = 0, 1, \ldots, W$, niech $P(i, w)$ oznacza problem wypełnienia plecaka o pojemności $w$ używając jedynie przedmiotów o indeksach ściśle mniejszych od $i$. W szczególności:

• $P(0, w)$ oznacza problem wypełnienia plecaka nie mając do dyspozycji żadnych przedmiotów.
• $P(n, W)$ oznacza oryginalny problem.

Niech $V(i, w)$ oznacza wartość (dowolnego) optymalnego rozwiązania $P(i, w)$. Opiszmy teraz, w jaki sposób szukanie optymalnego rozwiązania $P(i, w)$ redukuje się do znajdowania optymalnych rozwiązań podproblemów, i jakie zależności rekurencyjne wynikają z tego dla funkcji $V(i, w)$.

Przypadek 1. Jeśli $i = 0$, to dla dowolnego $w$, jedyne rozwiązanie $P(i, w)$ to pakowanie puste. Stąd $V(0, w) = 0$ dla wszystkich $w$.

Przypadek 2. Załóżmy, że $i > 0$. Rozważmy ostatni z dostępnych przedmiotów (o indeksie $i-1$). Jeśli jego waga $w_{i-1}$ przekracza pojemność $w$ plecaka z podproblemu, wówczas optymalne rozwiązanie $P(i, w)$ używa jedynie przedmiotów o indeksach $0, 1, \ldots, i - 2$, a zatem jest tożsame z optymalnym rozwiązaniem $P(i - 1, w)$. W tym przypadku $V(i, w) = V(i - 1, w)$.

Przypadek 3. Ostatnią możliwością jest $i > 0$ i $w_{i-1} \leq w$. Wtedy są dwie możliwości:

• Optymalne rozwiązanie $P(i, w)$ nie używa przedmiotu $i-1$. Wtedy (tak, jak w poprzednim przypadku), rozwiązanie to jest tożsame z optymalnym rozwiązaniem $P(i-1, w)$. Wtedy wartość rozwiązania to $V(i - 1, w)$.
• Optymalne rozwiązanie $P(i, w)$ używa przedmiotu $i-1$. Wtedy, po umieszczeniu w plecaku tego przedmiotu, pozostała część plecaka ma pojemność równą $w - w_{i-1}$ i musi być ona w optymalny sposób wypełniona pozostałymi z dostępnych przedmiotów (o indeksach mniejszych, niż $i-1$). To optymalne wypełnienie to dokładnie optymalne rozwiązanie $P(i - 1, w - w_{i-1})$. Wartością takiego rozwiązania $P(i, w)$ jest $v_{i-1} + V(i - 1, w_{i-1})$.

Optymalnym rozwiązaniem $P(i, w)$ jest to, dla którego uzyskana wartość jest największa. Stąd mamy też: $$V(i, w) = \max\big( V(i - 1, w), v_{i-1} + V(i - 1, w_{i-1}) \big).$$

Budowa rozwiązania metodą wstępną. Konstruujemy macierz rozmiaru $(n+1) \times (W + 1)$, w której element z $i$-tego wiersza i $w$-tej kolumny jest równy $V(i, w)$:

Wiersz $0$ wypełniamy zerami, zgodnie z warunkiem $V(0, w) = 0$ dla wszystkich $w$. Do wypełnienia kolejnych wierszy, wystarczą nam wartości z wiersza poprzedniego. Przykładowa implementacja, wraz z testem (przykładowe przedmioty z początku rozdziału):

import numpy as np


def knapsack(items, weight):
    n = len(items)
    cache = np.zeros((n + 1, weight + 1))

    for i in range(1, n + 1):
        for w in range(weight + 1):
            item_weight, item_value = items[i - 1]
            if item_weight > w:
                cache[i, w] = cache[i - 1, w]
            else:
                cache[i, w] = max(cache[i - 1, w], cache[i - 1, w - item_weight] + item_value)
    return cache[n, weight]

#        lampa    cormen    blender  koń        tytan    ozdoba   krzeslo  odkurzacz
items = [(2, 40), (2, 160), (3, 70), (15, 300), (1, 70), (4, 25), (5, 25), (6, 180)]

print(knapsack(items, 15))

520.0

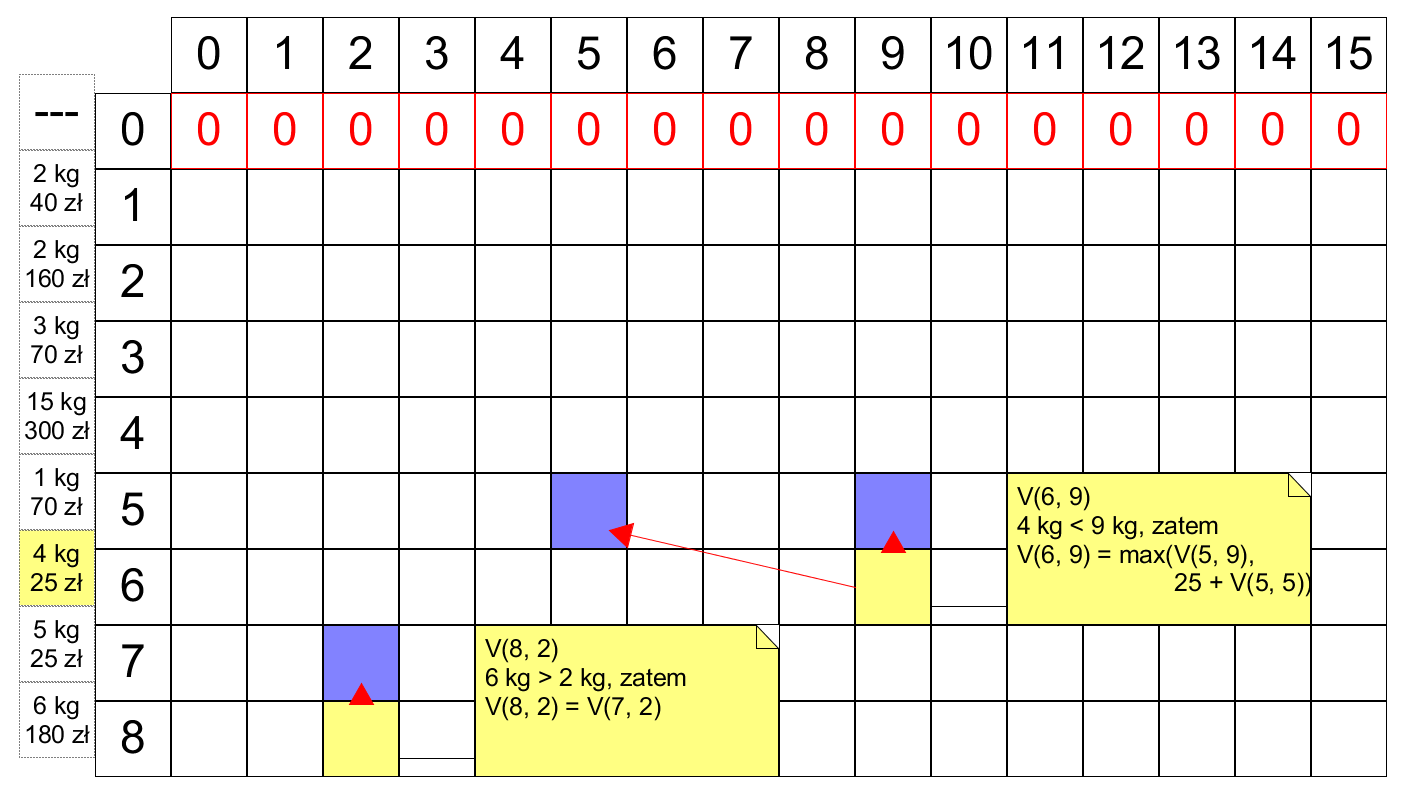
Rekonstrukcja szczegółowego rozwiązania. Powyżej, w funkcji knapsack, element cache[n, weight] zawiera wartość rozwiązania zadanego problemu. Aby odtworzyć listę przedmiotów, które się na nie składają, wystarczy odczytać, w jaki sposób powstają wartości elementów macierzy. Dla danych z przykładu, pełna macierz wygląda następująco:

[[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] [ 0 0 40 40 40 40 40 40 40 40 40 40 40 40 40 40] [ 0 0 160 160 200 200 200 200 200 200 200 200 200 200 200 200] [ 0 0 160 160 200 230 230 270 270 270 270 270 270 270 270 270] [ 0 0 160 160 200 230 230 270 270 270 270 270 270 270 270 300] [ 0 70 160 230 230 270 300 300 340 340 340 340 340 340 340 340] [ 0 70 160 230 230 270 300 300 340 340 340 340 365 365 365 365] [ 0 70 160 230 230 270 300 300 340 340 340 340 365 365 365 365] [ 0 70 160 230 230 270 300 300 340 410 410 450 480 480 520 520]]

Element cache[8, 15] jest równy albo cache[7, 15] (gdy optymalne rozwiązanie nie używa ostatniego przedmiotu - odkurzacza), albo 180 + cache[7, 15-9] (gdy optymalne rozwiązanie tego odkurzacza używa). Widzimy, że zachodzi drugi z tych przypadków. Z kolei cache[7, 9] jest równe cache[6, 9], lecz nie 25 + cache[6, 4], zatem optymalne rozwiązanie nie używa przedmiotu przedostatniego (krzesła). Kontynuując to śledzenie, odtwarzamy rozwiązanie - identyczne, jak pod przykładem z początku rozdziału.

Modyfikację funkcji knapsack, implementującą odczytywanie tego rozwiązania, pomijamy.

Na koniec podrozdziału opiszemy złożoności tego algorytmu. Tak jak w przypadku pozostałych algorytmów "wstępnych", łatwo je wyznaczyć:

• Złożoność pamięciowa: równa rozmiarowi uzupełnianej macierzy, czyli $\Theta(nW)$.
• Złożoność czasowa: wyznaczenie elementu macierzy to stała ilość operacji, zatem również $\Theta(nW)$.

Interludium

W tym przerywniku poczynimy pewne uwagi dotyczące algorytmów dynamicznych.

1. Złożoność pamięciowa. W omówionym wyżej algorytmie rozwiązującym dyskretny problem plecakowy, wykorzystujemy macierz o asymptotycznym rozmiarze $\Theta(nW)$. Macierzy tej potrzebujemy jednak tylko do wyznaczenia szczegółowego rozwiązania. Gdyby interesowała nas jedynie wartość optymalnego rozwiązania (czyli wartość ostatniego elementu ostatniego wiersza), a nie konkretny sposób jego uzyskania, możemy dokonać wyliczeń w bardziej pamięciowo oszczędny sposób. Zwróciliśmy już uwagę, że do skonstruowania wartości wiersza $i+1$ wystarczą nam jedynie wartości z wiersza $i$. Oznacza to, że w każdym momencie obliczeń wystarczy pamiętać jedynie dwa ostatnie wiersze macierzy: obecnie wyliczany, i ten wyliczony wcześniej (istnieje też prosty sposób, w którym wystarczy pamiętać jeden wiersz, i ciągle nadpisywać jego wartości). To redukuje wymagania pamięciowe do $\Theta(W)$.

Bardzo podobny zabieg można wykonać w problemie $LCS$, gdzie macierz również wypełniamy wiersz po wierszu. Tam redukcja pamięci może być znaczna: złożoność pamięciowa $\Theta(nm)$ (gdzie $n$ i $m$ to długości ciągów), redukuje się do $\Theta(\min(n, m))$ (możemy bowiem założyć, że drugi z ciągów jest nie dłuższy niż pierwszy, w razie potrzeby zamieniając je miejscami). W praktyce, dla ciągów długości dziesiątek czy setek tysięcy (np. fragmentów DNA), typowo redukuje to (faktyczne) wymogi pamięciowe z setek gigabajtów do zaledwie drobnych megabajtów. Pamięć przestaje być wtedy ograniczeniem na działanie algorytmu - pozostaje nim czas.

2. Optymalna podstruktura. Nie każdy problem optymalizacyjny ma własność optymalnej podstruktury. Skontrastujmy tu dwa problemy, dotyczące ścieżek w grafach skierowanych bez cykli o ujemnej wadze:

Problem najkrótszej ścieżki ma własność optymalnej podstruktury. Niech $t \neq s$ będą wierzchołkami połączonymi ścieżką. Rozważmy najkrótszą scieżkę $S$ prowadzącą z $t$ do $s$. Oznaczmy przez $v_0, v_1, \ldots, v_n$ poprzedniki $s$ (czyli wierzchołki, z których wychodzi krawędź prowadząca do $s$). Wtedy przedostatnim wierzchołkiem, przez który przechodzi $S$ jest jeden z wierzchołków $v_i$. Odcinając z $S$ ostatnią krawędź $(v_i, s)$, otrzymujemy ścieżkę $S'$ z $t$ do $v_i$. Musi to być najkrótsza taka ścieżka: gdyby istniała ścieżka $S''$ z $t$ do $v_i$ krótsza od $S'$, wówczas $S''$ uzupełniona o $(v_i, s)$ byłaby ścieżką z $t$ do $s$ krótszą niż $S$ - sprzeczność.

Znalezienie najkrótszej (optymalnej) ścieżki z $t$ do $s$ sprowadza się zatem do znalezienia najkrótszych ścieżek z $t$ do $v_0, v_1, \ldots, v_n$, uzupełnienia ich o krawędzie prowadzące do $s$, oraz wybrania najkrótszej z nich. Wyróżnionym w ten sposób podproblemem jest $P(v)$ - "znalezienie najkrótszej ścieżki z $t$ do $v$". Funkcją opisującą wartość rozwiązania $P(v)$ jest długość tej ścieżki. Wyróżnionych tak podproblemów nie jest wiele - tyle, co wierzchołków w grafie. Sugeruje to, że istnieje pewien algorytm dynamiczny, rozwiązujący problem najkrótszych ścieżek w grafach skierowanych ważonych bez cykli o ujemnej wadze - rzeczywiście, takim algorytmem jest np. algorytm Bellmana-Forda (można nadmienić, że R. Bellman był twórcą koncepcji programowania dynamicznego).

Problem najdłuższej ścieżki bez cykli. Niech $t \neq s$ będą wierzchołkami połączonymi ścieżką. Zadaniem jest znalezienie najdłuższej ścieżki z $t$ do $s$, która każdy wierzchołek odwiedza co najwyżej raz. Na pierwszy rzut oka, problem wydaje się zbliżony do problemu szukania najkrótszej ścieżki, jednak nie ma on własności optymalnej podstruktury - a przynajmniej nie w sposób opisany w poprzednim przykładzie. Rozważmy następujący graf (wagi wszystkich krawędzi to $1$):

Wówczas jedyna najdłuższa ścieżka bez cykli z $A$ do $B$ to ścieżka przechodząca kolejno przez wierzchołki $A, D, C, B$. Są też dwie najdłuższe takie ścieżki z $A$ do $C$: ta, przechodząca przez kolejno $A, B, C$, oraz ta przechodząca przez $A, D, C$. Zwróćmy jednak uwagę, że żadna z tych dwóch ścieżek nie powstaje przez wzięcie najdłuższej ścieżki bez cykli do poprzednika $C$ i uzupełnienie jej o krawędź do $C$. Najdłuższa ścieżka bez cykli z $A$ do $B$ uzupełniona o krawędź prowadzącą do $C$ nie jest bowiem ścieżką bez cykli. Analogicznie dla $D$ w miejscu $B$.

Optymalne mnożenie ciągu macierzy

Opis problemu

Niech $A$ i $B$ będą macierzami (na przykład o współczynnikach rzeczywistych) o wymiarach $a \times b$ i $b \times c$ odpowiednio. Macierze te są kompatybilnych rozmiarów: można je ze sobą pomnożyć. Iloczyn $AB$ jest macierzą rozmiaru $a \times c$. Rozważmy koszt wyliczenia takiego iloczynu. Każdy współczynnik $AB$ jest iloczynem skalarnym jednego z wierszy $A$ z odpowiednią kolumną $B$. Wykonanie tego iloczynu wymaga $b$ mnożeń skalarnych (tzn. mnożeń współczynników) oraz $b-1$ dodawań. W sumie dostajemy zatem $abc$ mnożeń i $ac(b-1)$ dodawań.

W arytmetyce cyfrowej, mnożenie jest z reguły znacznie kosztowniejszą operacją niż dodawanie - dobrą analogią jest tu koszt potrzebny na dodanie lub pomnożenie liczb na kartce papieru, w słupku. Z tego powodu, koszt operacji jak powyżej często wyraża się tylko ze względu na ilość wymaganych mnożeń. Przyjmiemy zatem, że koszt mnożenia macierzy podanych wyżej rozmiarów to $abc$ mnożeń (skalarnych).

Niech teraz $C$ będzie macierzą rozmiaru $c \times d$. Iloczyn macierzy $ABC$ ma wtedy sens i jego wynik to macierz rozmiaru $a \times d$. Wyznaczmy koszt wyliczenia tego iloczynu. Mnożenie macierzy jest operacją łączną (wynik nie zależy od nawiasowania). Mamy więc dwa sposoby wyliczenia:

• Opcja 1: wyliczamy iloczyn $AB$ kosztem $abc$ mnożeń, uzyskując macierz $a \times c$. Następnie wyliczamy $(AB)C$ kosztem $acd$ mnożeń.
• Opcja 2: wyliczamy iloczyn $BC$ kosztem $bcd$ mnożeń, uzyskując macierz $b \times d$. Następnie wyliczamy $A(BC)$ kosztem $abd$ mnożeń.

Opcja pierwsza kosztuje w sumie $abc + acd$ mnożeń, druga zaś $bcd + abd$ mnożeń. Nie są to wyrażenia tożsame. Dla przykładowych wartości $a = 10, b = 20, c = 15, d = 15$, otrzymujemy koszty:

• Opcja 1: $3000 + 3750 = 6750$ mnożeń.
• Opcja 2: $7500 + 5000 = 12500$ mnożeń.

Wybór kolejności działań - czyli nawiasowania wyrażenia $ABC$ - nie zmienia wyniku, lecz zmienia koszt jego uzyskania (w tym przykładzie niemal dwukrotnie). Sytuacja staje się jeszcze bardziej skomplikowana, jeśli zwiększymy ilość macierzy w iloczynie.

Opiszmy zatem ogólną wersję problemu optymalnego mnożenia ciągu macierzy.

Dla $n > 0$, niech $(A_i)_{i < n}$ będzie ciągiem macierzy o kompatybilnych rozmiarach, aby miał sens iloczyn $A_0 A_1 \ldots A_{n-1}$.

Niech $h_i$ i $w_i$ oznaczają odpowiednio wysokość i szerokość macierzy $A_i$. Koniecznie mamy $w_i = h_{i+1}$.

Celem jest znalezienie kolejności działań w iloczynie $A_0 A_1 \ldots A_{n-1}$, aby koszt wyliczenia tego iloczynu był jak najmniejszy. Równoważnie: celem jest optymalne znawiasowanie tego iloczynu.

Sprawdźmy, że siłowe rozwiązanie problemu - przez sprawdzenie kosztów dla wszystkich możliwych nawiasowań - nie wchodzi w rachubę.

Fakt. Niech $T(n)$ będzie ilością wszystkich możliwych (parami nierównoważnych) nawiasowań w iloczynie długości $n$. Wtedy dla wszystkich $n > 1$ mamy $T(n+1) \geq 2T(n)$.
Dowód. W iloczynie $A_0 A_1 \ldots A_{n-1}$ możemy postawić nawiasy: $(A_0) (A_1 \ldots A_{n-1})$. Następnie dostawiając wszystkie nawiasowania podciągu $A_1 \ldots A_{n-1}$ otrzymujemy $T(n)$ nawiasowań. Analogicznie, możemy znawiasować ciąg kładąc nawiasy $(A_0 A_1 \ldots A_{n-2})(A_{n-1})$. Dostawiając wszystkie nawiasowania podciągu $A_0 A_1 \ldots A_{n-2}$ dostajemy następne $T(n)$ innych nawiasowań. $\dashv$

Prostym wnioskiem z powyższego Faktu jest stwierdzenie, że ilość parami nierównoważnych nawiasowań ciągu rośnie co najmniej wykładniczo wraz z jego długością.

Rozwiązanie w sposób dynamiczny

Ponownie stosujemy maszynerię programowania dynamicznego. Stosujemy oznaczenia, jak w sformułowaniu problemu.

Optymalna podstruktura i funkcja kosztu. Dla $0 \leq i \leq j < n$, niech $P(i,j)$ oznacza problem optymalnego mnożenia podciągu $A_i A_{i+1} \ldots A_j$. Niech $C(i, j)$ to koszt (ilość) mnożeń dla optymalnego rozwiązania $P(i,j)$. Wtedy:

• Główny problem jest tożsamy z $P(0, n-1)$.
• Problem postaci $P(i,i)$ to problem mnożenia ciągu złożonego z pojedynczej macierzy $A_i$: ma ono trywialne rozwiązanie.

Obserwujemy, że w każdym (niekoniecznie optymalnym) rozwiązaniu $P(i,j)$, jedno z mnożeń musi zostać wykonane jako ostatnie. Przyjmijmy, że jest to mnożenie pomiędzy macierzami $A_k$ a $A_{k+1}$, gdzie $i \leq k < j$.

Spośród rozwiązań $P(i,j)$ takich, w których mnożenie między $A_k$ a $A_{k+1}$ jest ostatnie, możemy wybrać to o najmniejszym możliwym koszcie. To rozwiązanie - czyli ustalenie kolejności mnożeń - zadaje również kolejność mnożeń na podciągu $A_1 \ldots A_k$. Nazwijmy tę indukowaną kolejność "obcięciem" rozwiązania $P(i,j)$ do podciągu $A_1 \ldots A_k$. Twierdzimy, że to obcięcie to optymalna kolejność wykonywania działań dla $A_1 \ldots A_k$. Rzeczywiście: gdyby istniała lepsza kolejność, wtedy w rozwiązaniu $P(i,j)$ można zastąpić jego obcięcie do $A_1 \ldots A_k$ przez taką lepszą kolejność, uzyskując lepsze rozwiązanie $P(i,j)$.

Analogicznie, "obcięcie" takiego rozwiązania $P(i,j)$ do ciągu $A_{k+1} \ldots A_j$ jest optymalną kolejnością dla tego podciągu.

Płynie stąd następujący wniosek: przy ustalonym $k$ jak wyżej, aby skonstruować optymalną kolejność mnożenia $A_i \ldots A_j$, przy założeniu, że ostatnim wykonanym mnożeniem ma być to pomiędzy $A_k$ a $A_{k+1}$, należy znaleźć optymalną kolejność dla ciągu $A_i \ldots A_k$ (czyli znaleźć optymalne rozwiązanie $P(i,k)$), następnie znaleźć optymalne rozwiązanie $P(k+1, j)$, i złożyć te rozwiązania w rozwiązanie $P(i, j)$. Koszt takiego rozwiązania to suma kosztów rozwiązań $P(i,k)$ oraz $P(k+1, j)$, powiększona o koszt ostatniego mnożenia $(A_1 \ldots A_k)(A_{k+1} \ldots A_j)$. Całkowitym kosztem jest więc $C(i,k) + C(k+1,j) + h_iw_kw_j$. Ostatni składnik sumy to koszt mnożenia macierzy rozmiaru $h_i \times w_k$ (wynik mnożenia $A_1 \ldots A_k$) oraz macierzy rozmiaru $w_k \times w_j$ (wynik mnożenia $A_{k+1} \ldots A_j$).

Aby znaleźć optymalne rozwiązanie $P(i,j)$ wystarczy zatem, dla wszystkich $i \leq k < j$, znaleźć optymalne rozwiązania $P(i,k)$ i $P(k+1,j)$ i spośród nich wybrać to, które daje najtańsze rozwiązanie problemu $P(i,j)$.

Powyższe obserwacje nakładają następujące warunki na $C(i, j)$:

• $C(i, i)$ = 0 dla wszystkich $i$.
• Gdy $i < j$, $C(i, j) = \min\{ C(i,k) + C(k+1,j) + h_i w_k w_j : i \leq k < j\}$.

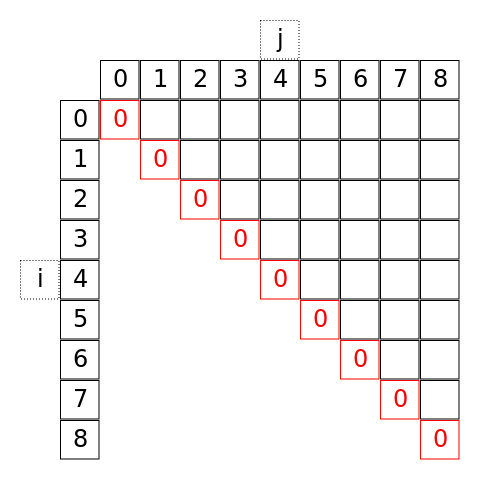
Budowa rozwiązania metodą wstępną. Konstruujemy macierz rozmiaru $n \times n$, w której element z $i$-tego wiersza i $j$-tej kolumny jest równy $C(i, j)$. Rysunki pokazują sytuację dla $n=9$. Wykorzystujemy tylko elementy macierzy na przekątnej i wyżej:

Do wyznaczenia elementu macierzy potrzebne są nam wszystkie elementy pod nim i wszystkie na lewo od niego:

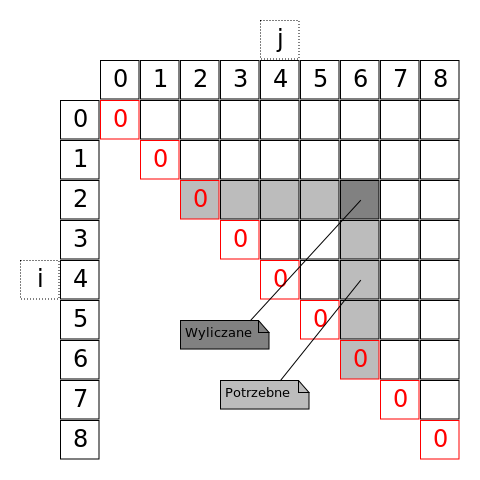
Sugeruje to dwie naturalne kolejności uzupełniania macierzy. My wybierzemy następującą:

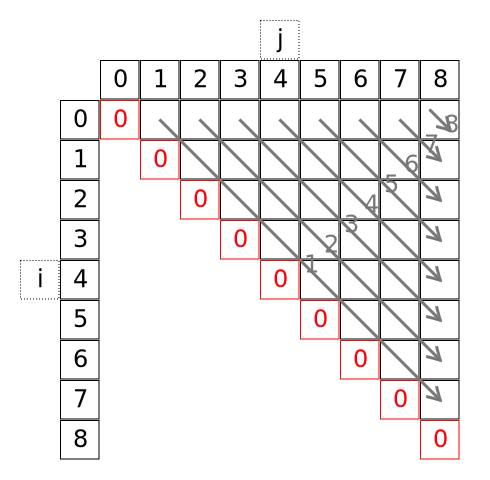
Każda tak oznaczona "nadprzekątna" zawiera koszty rozwiązań dla coraz dłuższych podciągów macierzy. Na przekątnej (wypełnionej zerami) są to koszty mnożeń ciągów złożonych z pojedynczej macierzy, na nadprzekątnej wyżej koszty mnożeń ciągów $A_1 A_2, A_2 A_3, \ldots, A_{n-2}A_{n-1}$, etc. Ostatnim uzupełnionym wyrazem jest odpowiadający $C(0, n-1)$.

Poniżej implementacja i przykład:

def matchain(shapes):
    n = len(shapes)
    cache = np.zeros((n, n), dtype=int)

    for j0 in range(1, n):
        for i in range(n - j0):
            j = j0 + i
            cache[i, j] = min(cache[i, k] + cache[k + 1, j] +
                              shapes[i][0] * shapes[k+1][0] * shapes[j][1] for k in range(i, j))

    return cache[0, n -1]


shapes = [(30, 10), (10, 20), (20, 40), (40, 15), (15, 25)]
print(matchain(shapes))

25250

Jak zawsze, algorytm można uzupełnić o odczytanie szczegółowego optymalnego rozwiązania, co pominiemy.

Zanim przejdziemy do wyznaczenia złożoności tego algorytmu, rozważmy jego prostą modyfikację. W oryginalnie postawionym problemie, szukamy kolejności działań, która minimalizuje koszt wyrażony w wykonanych mnożeniach. Możemy jednak odwrócić problem i zapytać o kolejność działań, w której tych mnożeń wykonujemy najwięcej. Tak powstawiony problem jest niemal identyczny z oryginalnym (ma własność optymalnej podstruktury, z analogicznym uzasadnieniem). Jedyna różnica przy konstrukcji optymalnego rozwiązania $P(i,j)$ polega na tym, że wybieramy optymalne rozwiązania $P(i,k)$ i $P(k+1,j)$ dające największy koszt zamiast najmniejszego. W rekurencyjnej definicji funkcji kosztu odpowiada to zastąpieniu $\min$ przez $\max$. Podobnie, algorytm rozwiązujący tak zmodyfikowany problem jest identyczny z powyższym, ale z min zastąpionym przez max:

def matchain_worst_cost(shapes):
    n = len(shapes)
    cache = np.zeros((n, n), dtype=int)

    for j0 in range(1, n):
        for i in range(n - j0):
            j = j0 + i
            cache[i, j] = max(cache[i, k] + cache[k + 1, j] +
                              shapes[i][0] * shapes[k+1][0] * shapes[j][1] for k in range(i, j))

    return cache[0, n -1]


shapes = [(30, 10), (10, 20), (20, 40), (40, 15), (15, 25)]
print(matchain_worst_cost(shapes))

75000

W podanym wyżej przykładzie - mnożenia pięciu macierzy dość skromnych rozmiarów - różnica między optymalną a najgorszą kolejnością wykonywania działań jest prawie trzykrotna. Możemy zgadywać, że obranie jakiejkolwiek strategii mnożenia innej niż optymalna będzie kosztować wiele tysięcy operacji mnożeń.

Przejdziemy teraz do wyznaczenia złożoności algorytmów, oraz końcowego komentarza.

• Złożoność pamięciowa: równa rozmiarowi uzupełnianej macierzy, czyli $\Theta(n^2)$.
• Złożoność czasowa: czas wyznaczenia wyrazu macierzy zależy od jego indeksów. Dla wyrazu o współrzędnych $i, j$ jest to $(j-i)$ operacji. Złożoność wynosi zatem $$\sum_{i < j} (j - i) = \sum_{k=1}^{n-1}k(n-k) \in \Theta(n^3).$$

Uwaga. Licząc dokładnie ilość mnożeń, potrzebnych do obliczenia optymalnego mnożenia ciągu długości $n$, otrzymujemy liczbę $\frac{(n-1)n(n+1)}{3} \approx \frac{n^3}{3}$. Nie zależy ona od rozmiarów macierzy, a jedynie ich ilości. Dla pięciu macierzy - jak w przykładzie powyżej - oznacza to koszt zaledwie $40$ mnożeń. Widać jednak, że zysk przy samym mnożeniu macierzy był znaczny (rzędu dziesiątek tysięcy mnożeń).

Dyskretny problem plecakowy - wersja minimum

Pod koniec poprzedniego podrozdziału zauważyliśmy, że rozwiązanie problemu najtańszego mnożenia ciągu macierzy można łatwo przerobić na rozwiązanie problemu najdroższego mnożenia. Na zakończenie tego rozdziału skryptu dokonamy podobnego zabiegu dla problemu plecakowego. Rozważmy następującą jego wersję:

Przy oznaczeniach jak w dyskretnym problemie plecakowym, szukamy podzbioru $J \in \{0, 1, \ldots, n-1\}$ tak, aby:

1. $\sum_{j \in J} w_j = W$,
2. $\sum_{j \in J} v_j$ było możliwie najmniejsze.

Jak wcześniej, zbiór indeksów $J$ spełniający warunek 1. będziemy nazywać rozwiązaniem dopuszczalnym. Każde rozwiązanie dopuszczalne spełniające warunek 2. nazwiemy rozwiązaniem optymalnym. Sumę $\sum_{j \in J} v_j$ nazwiemy wartością rozwiązania.

Zwracamy uwagę na różnicę w warunku 1.: wybrane przedmioty muszą wypełnić cały plecak. Oznacza to, że problem (lub podproblem $P(i,w)$, polegający na wypełnieniu plecaka przedmiotami o indeksach mniejszych od $i$) może w ogóle nie mieć rozwiązania. Rozważmy opis optymalnych rozwiązań $P(i,w)$.

Przypadek 1. Jedyne rozwiązanie $P(0, w)$ to pakowanie puste. Gdy $w = 0$, jest to rozwiązanie dopuszczalne. Gdy $w > 0$, $P(0, w)$ nie ma rozwiązań.

Przypadek 2. Załóżmy, że $i > 0$. Rozważmy ostatni z dostępnych przedmiotów (o indeksie $i-1$). Jeśli jego waga $w_{i-1}$ przekracza pojemność $w$ plecaka z podproblemu, wówczas optymalne rozwiązanie $P(i, w)$ używa jedynie przedmiotów o indeksach $0, 1, \ldots, i - 2$, a zatem jest tożsame z optymalnym rozwiązaniem $P(i - 1, w)$, o ile takie istnieje. W przeciwnym wypadku $P(i, w)$ nie ma rozwiązania.

Przypadek 3. Ostatnią możliwością jest $i > 0$ i $w_{i-1} \leq w$. Wtedy są trzy możliwości:

• Optymalne rozwiązanie $P(i, w)$ nie używa przedmiotu $i-1$. Wtedy (tak, jak w poprzednim przypadku), rozwiązanie to jest tożsame z optymalnym rozwiązaniem $P(i-1, w)$, o ile takie istnieje.
• Optymalne rozwiązanie $P(i, w)$ używa przedmiotu $i-1$. Wtedy, po umieszczeniu w plecaku tego przedmiotu, pozostała część plecaka ma pojemność równą $w - w_{i-1}$ i musi być ona w optymalny sposób wypełniona pozostałymi z dostępnych przedmiotów (o indeksach mniejszych, niż $i-1$). To optymalne wypełnienie to dokładnie optymalne rozwiązanie $P(i - 1, w - w_{i-1})$, o ile takie istnieje.
• Ani $P(i-1, w)$, ani $P(i - 1, w - w_{i-1})$ nie mają rozwiązań. Wtedy $P(i, w)$ nie ma rozwiązań.

Niech $C(i,w)$ oznacza koszt optymalnego rozwiązania $P(i,w)$, o ile takie istnieje. Niech w przeciwnym wypadku $C(i,w) = \infty$. Taki zabieg pozwala na zgrabne opisanie zależności rekurencyjnych między $C(i,w)$ wynikających z powyższych przypadków:

• $C(0, 0) = 0$
• $C(0, w) = \infty$ dla wszystkich $w > 0$.
• Jeśli $w_{i-1} > w$, to $C(i,w) = C(i-1,w)$.
• Jeśli $w_{i-1} \leq w$, to $C(i,w) = \min\big(C(i-1,w), v_{i-1} + C(i-1,w - w_{i-1}) \big)$.

Korzystamy tu z faktu, że $\infty$ jest elementem neutralnym działania $\min$. Przykładowa implementacja:

def knapsack_full_minimum(items, weight):
    n = len(items)
    cache = np.full((n + 1, weight + 1), np.Infinity)
    cache[0, 0] = 0

    for i in range(1, n + 1):
        for w in range(weight + 1):
            item_weight, item_value = items[i - 1]
            if item_weight > w:
                cache[i, w] = cache[i - 1, w]
            else:
                cache[i, w] = min(cache[i - 1, w], cache[i - 1, w - item_weight] + item_value)

    # print(cache)
    return cache[n, weight]


#        lampa    cormen    blender  koń        tytan    ozdoba   krzeslo  odkurzacz
items = [(2, 40), (2, 160), (3, 70), (15, 300), (1, 70), (4, 25), (5, 25), (6, 180)]

print(knapsack_full_minimum(items, 15))

230.0