G. Jagiella

Skrypt do wykładu Programowanie 2 (Python)

ostatnia modyfikacja: 31.10.2020

Wykład 11 - programowanie dynamiczne

Spis treści

• O rekurencjach i zapamiętywaniu
  • Minimalistyczny przykład
  • Usprawnienie fib przez schowek
  • Problemy z rekurencją i inna poprawka fib
• Najdłuższy wspólny podciąg
  • Opis problemu i pierwsze rozwiązania
  • Rozwiązanie metodą wstępną
• Programowanie dynamiczne

O rekurencjach i zapamiętywaniu

Uwaga ogólna. Z uwagi na ograniczenia techniczne składu tekstu, w skrypcie wszędzie utożsamiamy zmienne $n, m$ ze zmiennymi n, m odpowiednio.

Minimalistyczny przykład

Rozważmy dobrze już znany problem wyznaczania ciągu zadanego w rekurencyny sposób, a konkretnie ciągu Fibonacciego $(f_i)_{i \in \mathbb{N}}$ o początkowych wyrazach $f_0 = 0, f_1 = 1$. Nieefektywna implementacja wyznaczania $n$-tego wyrazu korzysta wprost z jego rekurencyjnej definicji:

def fib(n):
    if n in (0, 1):
        return n
    return fib(n - 1) + fib(n - 2)

print(fib(10))

55

Nieefektywność tej implementacji polega na nieakceptowalnym asymptotycznym czasie działania funkcji, który opiszemy poniżej. Każde wywołanie fib(n) dla n $> 1$ prowadzi do dwóch kolejnych rekurencyjnych wywołań funkcji. Rozważmy drzewo wywołań wywołania fib(5), w którym każdy węzeł reprezentuje wywołanie fib z danym parametrem, a węzeł jest w relacji rodzic-dziecko (kolejność zgodna z kolejnością wywołań) z każdym rekurencyjnym wywołaniem:

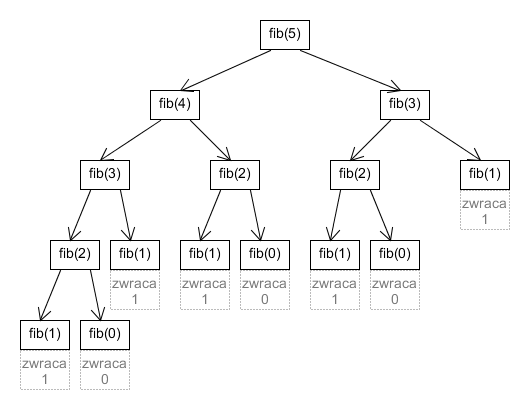
Tutaj fib(5) wywołuje fib(4), który wywołuje fib(3) etc. i dopiero po zakończeniu wywołań lewego poddrzewa fib(5) następuje wywołanie fib(3) z prawego poddrzewa, oraz rekurencyjnie węzłów pod nim. Podobnie dla każdego węzła. Stąd wywołania następują w kolejności zgodnej z trawersowaniem preorder.

Diagram wygląda podobnie dla każdego wywołania fib(n). Rozważmy złożoność czasową fib(n). Każde wywołanie fib, nie licząc czasu spędzonego w swoich rekurencyjnych wywołaniach, musi wykonać co najmniej jedno dodawanie. Złożoność czasowa będzie więc nie mniejsza, niż ilość węzłów w drzewie wywołań (przy założeniu, że dodawanie wykonuje się w czasie stałym, ten czas będzie dokładnie równy ilości węzłów). Oznaczmy przez $F(n)$ ilość węzłów w drzewie wywołań, dla którego korzeniem jest fib(n).

Fakt 1. $F(n) = 2 f_{n+1} - 1$.
Dowód Faktu 1 można znaleźć w dodatkowym materiale fib.pdf.

Rozwiązując rekurencję $f_{n+2} = f_{n+1} + f_{n}$ (metodami algebry liniowej lub kombinatoryki) stwierdzamy, że $f_n \sim \phi^n$ (gdzie $\phi = \frac{1 + \sqrt{5}}{2}$, złoty środek), skąd dostajemy opis złożoności czasowej algorytmu: wymaga on $\Theta(\phi^n)$ dodawań liczb typu int. Algorytmy działające w takim czasie (wykładniczym) nie są przydatne: można oszacować, że nawet na najszybszym sprzęcie, czas wyliczania fib(150) to co najmniej miliardy lat.

Opiszmy też wymagania pamięciowe. Każde wywołanie dowolnej funkcji wymaga utworzenia dla niej ramki wykonania (kontekstu), pamiętającego nazwy utworzone w funkcji oraz ich wartości. W szczególności, nowe ramki kolejnych wywołań fib(n) tworzą takie ramki. W chwili wywołania związanego z węzłem w drzewie wywołań, wywołanych funkcji jest tyle, ile jest przodków danego węzła, i tyle istnieje ramek. Każda ramka zawiera stałą ilość informacji (w uproszczeniu: tylko wartość parametru n odpowiedniego wywołania; tu zakładamy, że ta wielkość jest stała). Ramki są zapominane po wyjściu z rekurencyjnego wywołania. Najwięcej ramek jest pamiętanych w chwili wykonywania wywołań odpowiadających liściom drzewa i ich ilość jest równa wysokości drzewa. Najdłuższa gałąź w drzewie odpowiada zaś rekurencyjnemu ciągowi wywołań fib, czyli maksymalnej głębokości rekurencji: gałąź ta składa się z węzłów fib(n), fib(n-1), $\ldots$, fib(1). Stąd ilość pamięci potrzebna do przechowywania ramek jest proporcjonalna do $n$. Zatem złożoność pamięciowa algorytmu wynosi $\Theta(n)$.

Usprawnienie fib przez schowek

Łatwo zauważyć, że drzewo wywołań fib(n) zawiera wiele powtarzających się węzłów, a nawet całych poddrzew. Rzeczywiście: ilość unikalnych wywołań fib w takim drzewie to tylko n+1. Algorytm wykonuje zatem niepotrzebnie wiele pracy, wyliczając wielokrotnie wartość fib na tych samych argumentach, za każdym razem robiąc to w sposób rekurencyjny. Tymczasem wartość fib nie zależy od niczego, poza wartością parametru. Daje to pomysł na następujące usprawnienie algorytmu: po wyznaczeniu wartości fib(n) dla konkretnego n, zamiast po prostu zwrócić wartość, kładziemy ją do "schowka". Za każdym następnym wywołaniem fib(n), nie wyliczamy jej ponownie, a sięgamy po nią do schowka i zwracamy. "Schowkiem" będzie pewien słownik, którego kluczami i wartościami są pary n i fib(n). Słownik istnieje przez cały czas działania programu i elementy nigdy nie są z niego usuwane. Przykładowa implementacja (z pewną wadą, którą poprawimy):

# "cache", albo "schowek", początkowo stowarzyszający 0 i 1 z fib(0) i fib(1) odpowiednio.
# trzymanie cache w globalnym bloku to wspomniana wyżej wada
cache = {0: 0, 1: 1}

def fib(n):
    if n not in cache: # wartość fib(n) jeszcze nie zapamiętana w schowku? Liczmy ją więc:
        cache[n] = fib(n - 1) + fib(n - 2)
    return cache[n] # zwracamy wartość odczytaną ze schowka

print(fib(150))

9969216677189303386214405760200

Pierwsze wywołanie fib(n) dla n $> 1$ prowadzi do rekurencyjnego wyznaczenia wartości i zapamiętania jej w cache[n]. Stąd, każde następne wykonanie fib(n) dla tego samego n sprowadza się jedynie do testu n not in cache (i ominięcia wnętrza if) oraz zwrócenia cache[n], a obie te operacje wykonują się w czasie stałym. Rozważmy konsekwencję dla drzewa wywołań tak zdefiniowanego fib dla n $= 5$, zakładając, że jest to pierwsze wywołanie funkcji fib w ogóle. Po pierwszym wywołaniu fib(2) (węzła z lewej gałęzi drzewa - wywołania są wciąż zgodne z porządkiem preorder), rekurencyjnie wykonują się podwęzły fib(1) i fib(0), a gdy zwrócą odpowiednie wartości, fib(2) zapamięta je w schowku. Wszystkie następne wywołania fib(2) nie wywołają zatem fib(1) i fib(0) - możemy zatem usunąć z drzewa odpowiednie węzły (zaznaczamy stan po wyjściu z pierwszego wywołania fib(2):

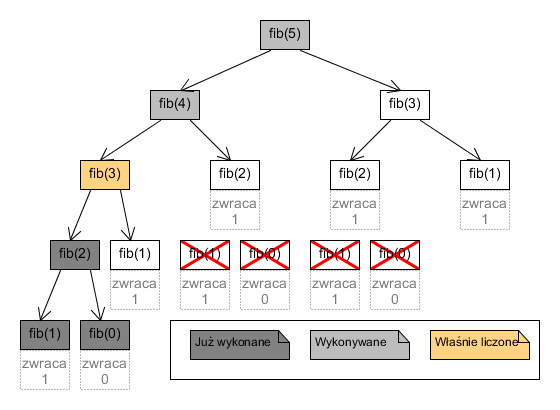
Analogicznie, po rekurencyjnym wywołaniu fib(1) w fib(3), zapamiętaniu wartości fib(3) i powrocie do fib(4):

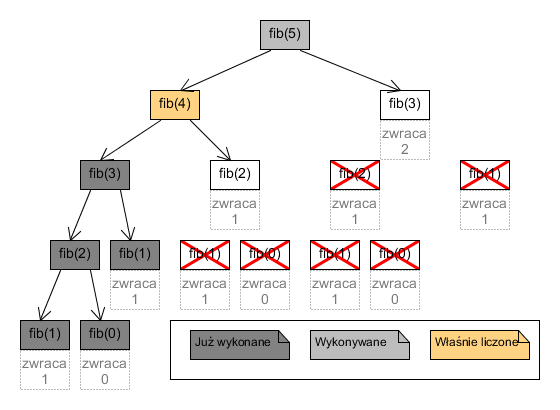
Po wyjściu z najwyższego poziomu rekurencji, węzły drzewa wywołań wyglądają więc następująco:

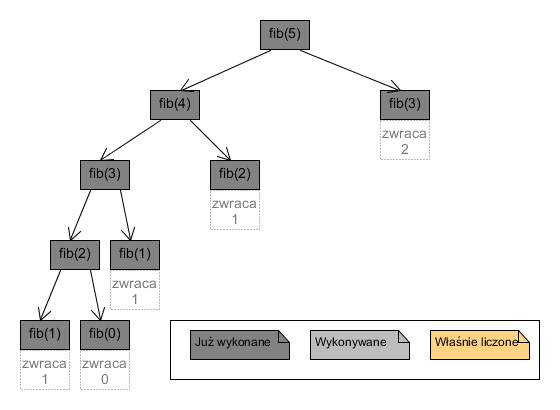
W drzewie pozostały więc jedynie: skrajna lewa gałąź, oraz prawe dziecko każdego węzła na tej gałęzi (poza ostatnim jej węzłem). Ten opis uogólnia się dla dowolnego $n$. Wykonanych węzłów jest zatem $2n - 1$.

Użycie schowka redukuje zatem złożoność czasową fib(n) do $\Theta(n)$ dodawań liczb int, cały czas zakładając, że jest to pierwsze wywołanie fib.

Podczas wyliczania fib(n), do schowka trafiły wszystkie wartości fib(m) dla m $<$ n. W konsekwencji, każde następne wywołanie fib skorzysta już z tych wartości, zatem jego rekurencyjne wyliczenie odwiedzi jeszcze mniej węzłów oryginalnego drzewa (czasem wręcz tylko jeden). Poprawnie będzie więc napisać, że złożoność to $O(n)$ dodawań zamiast $\Theta(n)$.

Maksymalna głębokość rekurencji tej wersji fib to również $O(n)$.

Złożoność pamięciowa schowka to $\Theta(n)$, gdzie $n$ to ilość przechowywanych wartości fib - tożsame z maksymalnym $n$, dla którego fib zostało wywołane w czasie działania programu.

Widzimy więc, że stosunkowo mało inwazyjny zabieg dodania schowka znacznie przyspieszył czas działania algorytmy z wykładniczego do liniowego kosztem konieczności przechowywania coraz większego schowka. Na zakończenie podrozdziału, poprawimy drobną wadę pierwotnej implementacji:

def fib(n, cache={0: 0, 1: 1}):
    if n not in cache: # wartość fib(n) jeszcze nie zapamiętana w schowku? Liczmy ją więc:
        cache[n] = fib(n - 1) + fib(n - 2)
    return cache[n] # zwracamy wartość odczytaną ze schowka

print(fib(150))

9969216677189303386214405760200

Używamy tu triku: uczyniliśmy z cache opcjonalny parametr fib z domyślną wartością będącą słownikiem - zmienialnym obiektem. Niektóre edytory ostrzegają przed takim działaniem: obiekt, który jest domyślną wartością parametru jest tworzony przy definiowaniu funkcji, a nie przy każdym jej wywołaniu, i jego modyfikacje przenoszą się na następne wywołania, jak w przykładzie niżej:

def f(lst=[]):
    lst.append(1)
    print(lst)
f()
f()
f()

[1]
[1, 1]
[1, 1, 1]

Używanie zmienialnych (mutowalnych) parametrów domyślnych często prowadzi do błędów. Jednak w fib jest ono jak najbardziej zgodne z intencją: pozwala na przetrzymywanie wartości schowka między kolejnymi wywołaniami, jednocześnie ukrywając schowek, usuwając go z globalnego bloku.

Problemy z rekurencją i inna poprawka fib

Algorytmy, które polegają na głębokich łańcuchach wywołań - przede wszyskim na głębokich rekurencjach - mają pewne ograniczenia. CPython ("domyślny", lub "standardowy" interpreter Pythona, którego używamy) arbitralnie ogranicza głębokość rekurencji do 1000 wywołań, częściowo celem ochrony przed nieskończonymi rekurencjami. Limit ten można zwiększyć, ale wtedy możemy napotkać inny problem. Bez przytaczania zbyt wielu szczegółów (dotyczących architektur sprzętu, systemów operacyjnych i interpretera): ramki wykonań kolejnych rekurencyjnych wywołań trafiają na tzw. stos procesu interpretera. Taki stos - przyznawany wykonywanym programom - ma bardzo ograniczony rozmiar w porównaniu do pamięci dostępnej w komputerze. Stąd łatwo ten stos przepełnić, prowadząc do "crashu" interpretera.

Z tego powodu, algorytmy oparte na rekurencji mogą napotkać na poważne ograniczenia maksymalnego rozmiaru danych. W przykładzie fib powyżej, głębokość rekurencji jest liniowo zależna od parametru (jest wręcz równa parametrowi). Wywołanie fib(1000) przekracza dopuszczalną głębokość. Istnieją problemy (o których traktuje wręcz ten rozdział skryptu), w których rozmiar danych rzędu tysięcy nie jest traktowany jako szczególnie duży, czyniąc algorytmy o proporcjonalnie głębokiej rekurencji mało użytecznymi.

Algorytmy rekurencyjne można przepisać na równoważne im algorytmy iteracyjne. Jest to dobra praktyka, pozwalająca na eliminację problemu przepełnienia stosu. Nie oznacza to jednak, że należy bezwględnie unikać algorytmów rekurencyjnych: są one bardzo przydatne np. w pracy na strukturach, których definicja jest rekurencyjna (na przykład drzewa, definiowane jako trójka: korzeń, lewe poddrzewo, prawe poddrzewo). Głębokość rekurencji nie stanowi większego problemu, jeśli możemy ją ograniczyć. Jako regułę można przyjąć, że jeśli głębokość rośnie logarytmicznie z rozmiarem danych, to rekurencja jest "bezpieczna": przykładem jest rekurencja w algorytmach sortowania. W mergesort, sortowana lista jest dzielona na połowy, na których rekurencyjnie wykonywany jest mergesort, dopóki listy nie zmaleją do trywialnych rozmiarów. Zagnieżdżonych rekurencji nie będzie więc więcej, niż możliwa ilość przepołowień, czyli $\log n$, gdzie $n$ to długość pierwotnej listy. Rekurencja głębokości $\approx 300$ zostałaby osiągnięta dopiero dla list o długości większej niż ilość atomów w obserwowalnym Wszechświecie.

Przykładami operacji, w których rekurencja ma logarytmicznie ograniczoną głębokość są też operacje kopcowania, oraz operacje na stosownie zbalansowanych drzewach binarnych (drzewach o logarytmicznej wysokości).

Z drugiej strony, przykładem znanego algorytmu, który na wykładzie był opisywany rekurencyjnie (ale również z wersją iteracyjną) jest przeszukiwanie grafu w głąb - głębokość rekurencji dla grafu o $n$ wierzchołkach to $O(n)$, co nie jest satysfakcjonujące.

Uwaga. CPython nie używa mechanizmu tzw. optymalizacji rekurencji ogonowej, polegającej na automatycznym zastąpieniu pewnych rekurencji przez równoważną pętlę.

Dokonajmy poprawki funkcji fib aby uzyskać funkcjonalność wersji rekurencyjnej ze schowkiem, ale bez konieczności rekurencyjnych wywołań:

def fib(n, cache=[0, 1]):
    for _ in range(n - len(cache) + 1):
        cache.append(cache[-1] + cache[-2])
    return cache[n]

print(fib(150))

9969216677189303386214405760200

Tutaj cache to lista, a nie słownik. Wartości fib w jej kolejnych indeksach konstruujemy metodą wstępną (wstępującą, bottom-up). Pierwsze dwie linijki funkcji gwarantują, że długość cache będzie większa, niż n, wykonując minimum potrzebnych do tego operacji (często zero iteracji pętli).

Najdłuższy wspólny podciąg

Opis problemu i pierwsze rozwiązania

Niech $(a_i)_{i < n} = (a_0, a_1, \ldots, a_{n-1})$ i $(b_i)_{i < m} = (b_0, b_1, \ldots, b_{m-1})$ będą skończonymi ciągami dowolnych obiektów (ciągi zawsze indeksujemy od $0$). Wspólnym podciągiem $(a_i)$ i $(b_i)$ nazywamy ciąg, który jest jednocześnie podciągiem $(a_i)$ i podciągiem $(b_i)$. Odcinkiem początkowym $(a_i)_{i < n}$ nazwiemy dowolny podciąg złożony z pewnej liczby jego początkowych elementów, czyli ciąg $(a_i)_{i<k}$ dla pewnego $0 \leq k \leq n$.

Problem najdłuższego wspólnego podciągu (LCS, longest common subsequence) polega na wskazaniu długości najdłuższego wspólnego podciągu podanych ciągów, oraz przykładu podciągu zaświadczającej o tej długości.

Przykład. Najdłuższy wspólny podciąg napisów (ciągów znaków) ALGORYTM i GRAMOTY ma długość $3$. Przykłady takich podciągów:

• AOY: ALGORYTM GRAMOTY
• AOT: ALGORYTM GRAMOTY
• GOT: ALGORYTM GRAMOTY
• etc.

Przykładem problemu najdłuższego wspólnego podciągu jest wyznaczanie podobieństwa między łańcuchami DNA (ciągami zasad ACGT), gdzie długie wspólne podciągi wskazują na pokrewieństwo genetyczne.

Naiwne rozwiązanie, polegające na przetestowaniu wszystkich podciągów $(a_i)_{i<n}$, sprawdzając, czy są podciągami $(b_i)$, oraz wybraniu najdłuższego z nich wymaga co najmniej $2^n$ operacji, zatem poszukujemy lepszego pomysłu.

Dla ciągów $a = (a_i)$ i $b = (b_i)$, wprowadźmy następujące oznaczenia, których będziemy używać do końca rozdziału o problemie:

• Przez $P(a, b)$ oznaczymy problem najdłuższego wspólnego podciągu $a$ i $b$ (nie jego rozwiązanie, ani nie długość takiego ciągu; będziemy odnosić się np. do "rozwiązania $P(a, b)$".
• Najdłuższy wspólny podciąg $a$ i $b$ jest optymalnym rozwiązaniem $P(a, b)$.
• Przez $LCS(a, b)$ oznaczymy długość najdłuższego wspólnego podciągu ciągów $a$ i $b$, czyli optymalnego rozwiązania $P(a, b)$.

Pokażemy teraz, że optymalne rozwiązanie $P(a, b)$ daje się opisać przy pomocy optymalnych rozwiązań problemów postaci $P(c, d)$, gdzie $c$ i $d$ to pewne odcinki początkowe $a$ i $b$ odpowiednio. Rozważmy następujące przypadki:

Przypadek 1. Jeden z ciągów $a, b$ jest pusty. Wtedy jedynym wspólnym podciągiem $a$ i $b$ jest ciąg pusty.

Przypadek 2. Ciągi $a$ i $b$ się niepuste i kończą się innym elementem. Oznaczmy przez $a'$ i $b'$ ciągi powstałe przez usunięcie ostatniego elementu z $a$ i $b$ odpowiednio. Oznaczmy też ostatnie elementy $a$ i $b$ przez $X$ i $Y$ i zapiszmy $a = a'X$ i $b = b'Y$. Zakładamy $X \neq Y$. Rozróżniamy przy tym $X$ i $Y$ od ich innych wystąpień w obu ciągach. Stwierdzamy:

Fakt A. Jeśli $c = (c_i)$ jest wspólnym podciągiem $a$ i $b$, to $X$ nie jest ostatnim elementem $c$ lub $Y$ nie jest ostatnim elementem $c$.
Dowód. Oczywiste: gdyby było inaczej, wtedy $X = Y$.$\dashv$

Fakt B. Jeśli $c$ jest najdłuższym wspólnym podciągiem $a$ i $b$, to $c$ jest najdłuższym wspólnym podciągiem $a'$ i $b$, lub $c$ jest najdłuższym wspólnym podciągiem $a$ i $b'$.
Dowód. Z poprzedniego faktu, $c$ nie kończy się $X$ lub nie kończy się $Y$. Bez straty ogólności załóżmy to pierwsze. Wtedy $c$ jest wspólnym podciągiem $a'$ i $b$. Jeśli istnieje ciąg $d$, który jest wspólnym podciągiem $a'$ i $b$ dłuższym niż $c$, wtedy jest on też wspólnym podciągiem $a$ i $b$ przeczącym temu, że $c$ jest najdłuższym takim ciągiem. $\dashv$

Powyższe pokazują, że optymalne rozwiązanie $P(a, b)$ jest optymalnym rozwiązaniem $P(a', b)$ lub jest optymalnym rozwiązaniem $P(a, b')$. Aby rozwiązać $P(a, b)$, wystarczy rozwiązać $P(a', b)$ i $P(a, b')$ i wybrać dłuższe z rozwiązań.

Przypadek 3. Ciągi $a$ i $b$ się niepuste i kończą się takim samym elementem. Używając oznaczeń jak w poprzednim przypadku, mamy $a = a'X, b=b'X$.

Fakt C. Istnieje ciąg $c$ będący najdłuższym wspólnym podciągiem $a$ i $b$ zakończonym $X$ (w obu z ciągów $a$ i $b$).
Fakt D. Jeśli $c$ jest podciągiem $a$ i $b$ z tezy Faktu D, to $c$ pozbawiony ostatniego elementu jest najdłuższym wspólnym podciągiem $a'$ i $b'$.
Dowody obu Faktów są zbliżone do dowodów z poprzedniego przypadku.

Oba Fakty pokazują, że optymalne rozwiązanie $P(a, b)$ powstaje przez wzięcie optymalnego rozwiązania $P(a', b')$ i dołączenie do niego $X$.

Zwracamy uwagę, że powyższe przypadki opisują jak sprowadzić optymalne rozwiązanie problemu najdłuższego wspólnego podciągu do prostszego podproblemu (lub podproblemów). Pozwalają też na rekurencyjny opis zależności między długościami podciągów. Przy oznaczeniach takich, jak w analizie przypadków:

1. Jeśli $a$ lub $b$ jest pusty: $LCS(a, b) = 0$. W przeciwnym wypadku:
2. Jeśli $X \neq Y$: $LCS(a, b) = \max\big(LCS(a', b), LCS(a, b')\big)$.
3. $LCS(a, b) = 1 + LCS(a', b')$.

Powyższe punkty 1., 2. i 3. zadają poprawny rekurencyjny schemat wyliczania funkcji $LCS$, który możemy zaimplementować z definicji:

def lcs(a, b):
    if len(a) == 0 or len(b) == 0:
        return 0
    if a[-1] != b[-1]:
        return max(lcs(a[:-1], b), lcs(a, b[:-1])) # tu dodatkowe nieefektywności - kopiowanie napisów
    return 1 + lcs(a[:-1], b[:-1]) # i tu też

print(lcs('ALGORYTM', 'GRAMOTY'))

3

Powyższa "naiwna" implementacja jest obarczona co najmniej dwoma problemami. Mniejszym jest dość nieefektywny sposób przekazywania odcinków początkowych (podnapisów) w rekurencyjnych wywołaniach lcs przez kopiowanie napisu (z pominięciem ostatniego znaku). Bardziej wydajnym sposobem byłoby przekazywanie oryginalnego napisu wraz z informacją, ile jego znaków stanowi przekazywany ciąg, unikając tej zbędnej kopii.

Większym problemem jest złożoność obliczeniowa wynikająca z samej rekurencyjnej natury algorytmu. Rozważmy przedstawione w przykładzie wywołanie lcs('ALGORYTM', 'GRAMOTY'), prowadzące do rekurencyjnych wywołań lcs('ALGORYTM', 'GRAMOTY') i lcs('ALGORYTM, GRAMOT'), etc. Pierwsze poziomy drzewa wywołań wyglądają więc następująco (w węzłach podajemy tylko parametry tych wywołań):

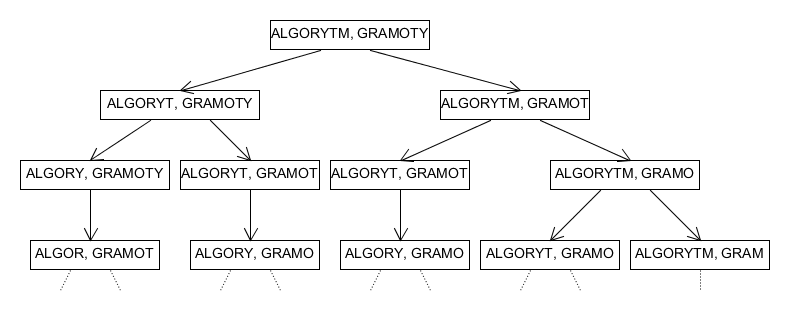
Nietrudno zauważyć, że gdyby początkowe ciągi nie zawierały wspólnych znaków, to każdy węzeł (inny niż liść) miałby dwa następniki. Sugeruje to wykładniczą złożoność algorytmu, podobnie jak w przypadku rekurencyjnego algorytmu dla ciągu Fibonacciego.

Kolejnym podobieństwem do rekurencyjnej wersji fib jest powtarzanie się wielu podproblemów. Rzeczywiście, par początkowych odcinków ciągów długości $n$ i $m$ jest dokładnie $(n+1) \cdot (m+1)$, a więc znacznie mniej, niż węzłów drzewa wywołań. Sugeruje to, że możemy zaadaptować metodę ze "schowkiem" również do poprawienia lcs.

# lcs ze schowkiem, wersja pierwsza - jeszcze do poprawki
def lcs(a, b, cache={}):
    n = len(a)
    m = len(b)
    if n == 0 or m == 0:
        return 0

    if (a, b) not in cache:
        if a[-1] != b[-1]:
            cache[a, b] = max(lcs(a[:-1], b), lcs(a, b[:-1]))
        else:
            cache[a, b] = 1 + lcs(a[:-1], b[:-1])
    return cache[a, b]

print(lcs('ALGORYTMALGORYTMALGORYTM', 'GRAMOTYGRAMOTYGRAMOTY'))

9

Powyższa wersja ma trzy wady. Pierwsza była już opisana i polega na nieefektywnym przekazywaniu podciągów przez branie kopii napisów. Druga wynika z typowego użycia lcs w programie, w którym wywołujemy lcs na wielu różnych parach ciągów. Każde wywołanie lcs z parametrami a1, b1 pozostawi w cache rozwiązanie wywołania lcs na wszystkich parach odcinków początkowych a1 i b1, co wprawdzie przyczyni się do zmniejszenia złożoności czasowej algorytmu, ale pozostawi w schowku dużo informacji, które przypuszczalnie nie przydadzą się przy wyliczaniu lcs na parach innych niż a1 i b1. Przydatny zatem byłby mechanizm, czyszczący schowek po rozwiązaniu głównego problemu. Trzecia wada jest związana z użyciem ciągów jako kluczy słownika cache, zamiast bardziej oszczędnej reprezentacji odcinków początkowych. Pierwszą wadę pozostawimy (usunięcie jej nie jest trudne), a ostatnie dwie wady usuniemy jednocześnie:

# lcs ze schowkiem, wersja druga
def lcs(a, b):
    cache = {}
    def lcs_inner(a, b):
        n = len(a)
        m = len(b)
        if n == 0 or m == 0:
            return 0

        if (n, m) not in cache:
            if a[-1] != b[-1]:
                cache[n, m] = max(lcs_inner(a[:-1], b), lcs_inner(a, b[:-1]))
            else:
                cache[n, m] = 1 + lcs_inner(a[:-1], b[:-1])
        return cache[n, m]
    return lcs_inner(a, b)

print(lcs('ALGORYTMALGORYTMALGORYTM', 'GRAMOTYGRAMOTYGRAMOTY'))

9

Ukrycie głównego rekurencyjnego algorytmu (lcs_inner) w zewnętrznej funkcji lcs pozwala na utworzenie nowego schowka za każdym wywołaniem lcs. W tej wersji, kluczami schowka są pary liczb - długości odcinków początkowych. Pary takie wymagają stałej ilości pamięci.

Rozważmy teraz złożoności ostatniej wersji algorytmu, którego parametrami są ciągu $a$, $b$ długości $n$, $m$ odpowiednio.

• Złożoność czasowa, z pominięciem nieefektywnego przekazywania podciągów, to ilość rekurencyjnych wywołań lcs_inner, równej ilości par odcinków początkowych $a, b$, czyli $\Theta(nm)$.
• Maksymalna głębokość rekurencji: każde rekurencyjne wywołanie lcs_inner skraca co najmniej jeden z ciągów o $1$, suma długości początkowych ciągów to $n+m$, a rekurencja kończy się, gdy jeden z ciągów jest pusty. Skrajnym przypadkiem jest sytuacja, gdy drugi z nich jest jednoelementowy. Aby uzyskać parę ciągu pustego i ciągu jednoelementowego zaczynając z $a$ i $b$, potrzeba $n+m-1$ skróceń, zatem szukana głębokość rekurencji to $O(n+m)$.
• Złożoność pamięciowa to pamięć potrzebna na schowek ($\Theta(nm)$) i wymagana pamięć związana z głębokością rekurencji ($O(n + m)$), razem $\Theta(nm)$.

Obserwujemy podobny zysk, jak w przypadku rekurencyjnego rozwiązania fib: znacznie redukujemy złożoność czasową algorytmu (z wykładniczej do wielomianu drugiego stopnia), kosztem zużycia pamięci. Podobnie nie rozwiązujemy jednak problemu rekurencji, której maksymalna głębokość jest liniowo zależna od długości wejściowych ciągów. Algorytmu nie będzie więc można stosować dla napisów długości tysięcy znaków (czyli np. niekoniecznie długich łańcuchów DNA).

Rozwiązanie metodą wstępną

Zaadaptujemy teraz metodę wstępną do problemu najdłuższego wspólnego podciągu. Dla ciągów $a, b$ rozmiarów odpowiednio $n, m$ zbudujemy macierz rozmiaru $(n + 1) \times (m + 1)$ w taki sposób, aby współczynnik $x_{i, j}$ odpowiadał wartości $LCS(c, d)$, gdzie $c$ jest odcinkiem początkowym $a$ długości $i$, a $d$ jest odcinkiem początkowym $b$ długości $j$. W szczególności, $x_{n,m} = LCS(a, b)$. Przykład macierzy (bez wyznaczonych wartości współczynników) dla $a=$ ALGORYTM i $b=$ GRAMOTY:

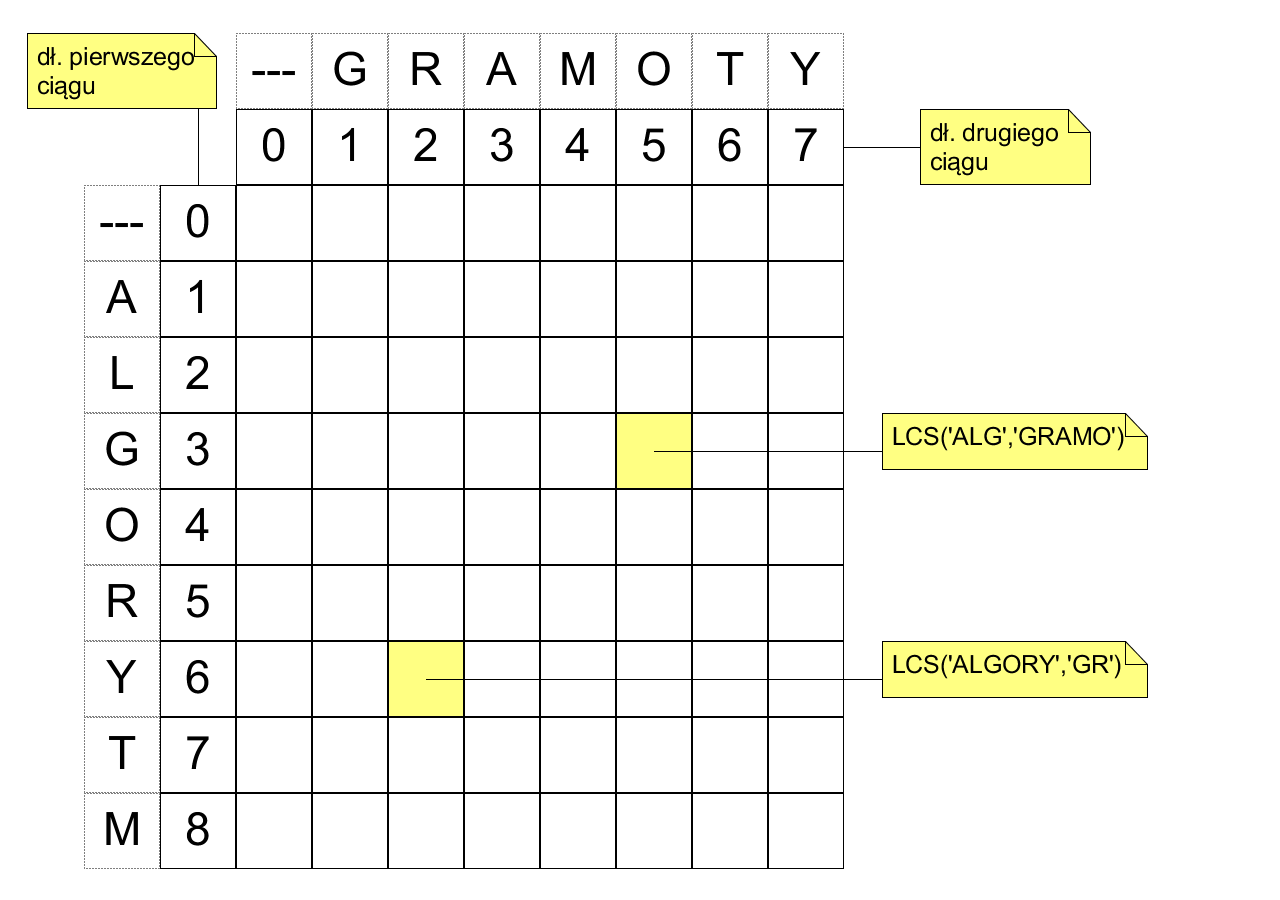
Łatwo wypełnić pierwszy wiersz i pierwszą kolumnę macierzy:

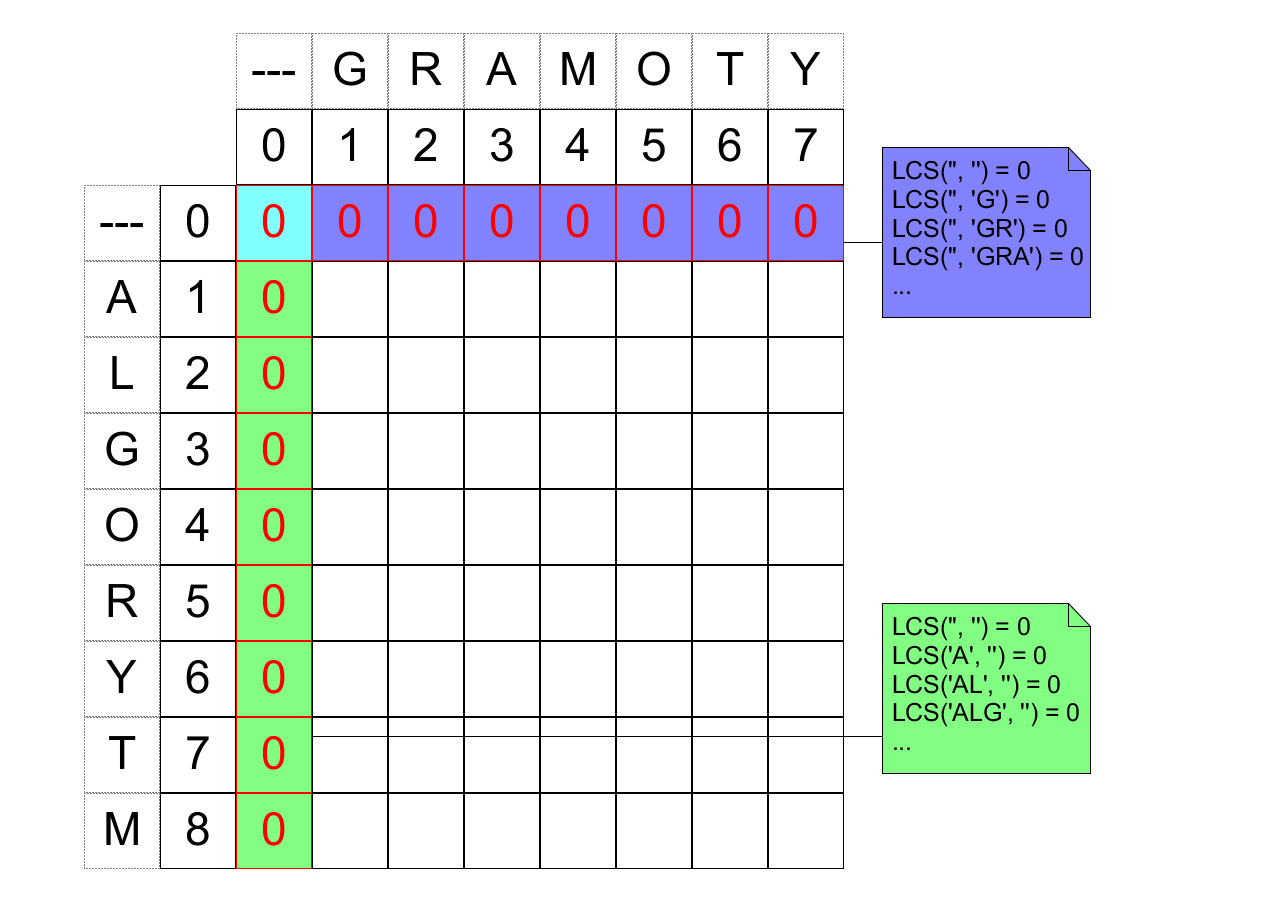
Rozważmy zależności pomiędzy współczynnikami macierzy, wynikającymi z rekurencyjnych zalezności między wartościami $LCS$.

• Jeśli współczynnik macierzy odpowiada wartości $LCS$ na ciągach zakończonych różnymi symbolami, jego wartość to maksimum współczynników nad nim i na lewo od niego (przypadek 2).
• Jeśli współczynnik macierzy odpowiada wartości $LCS$ na ciągach zakończonych tym samym symbolem, jego wartość to wartość współczynnika na lewo i w górę od niego, powiększona o $1$ (przypadek 3).

Graficznie, wyróżniamy dwa rodzaje współczynników: rodzaju "maksimum" i "+1":

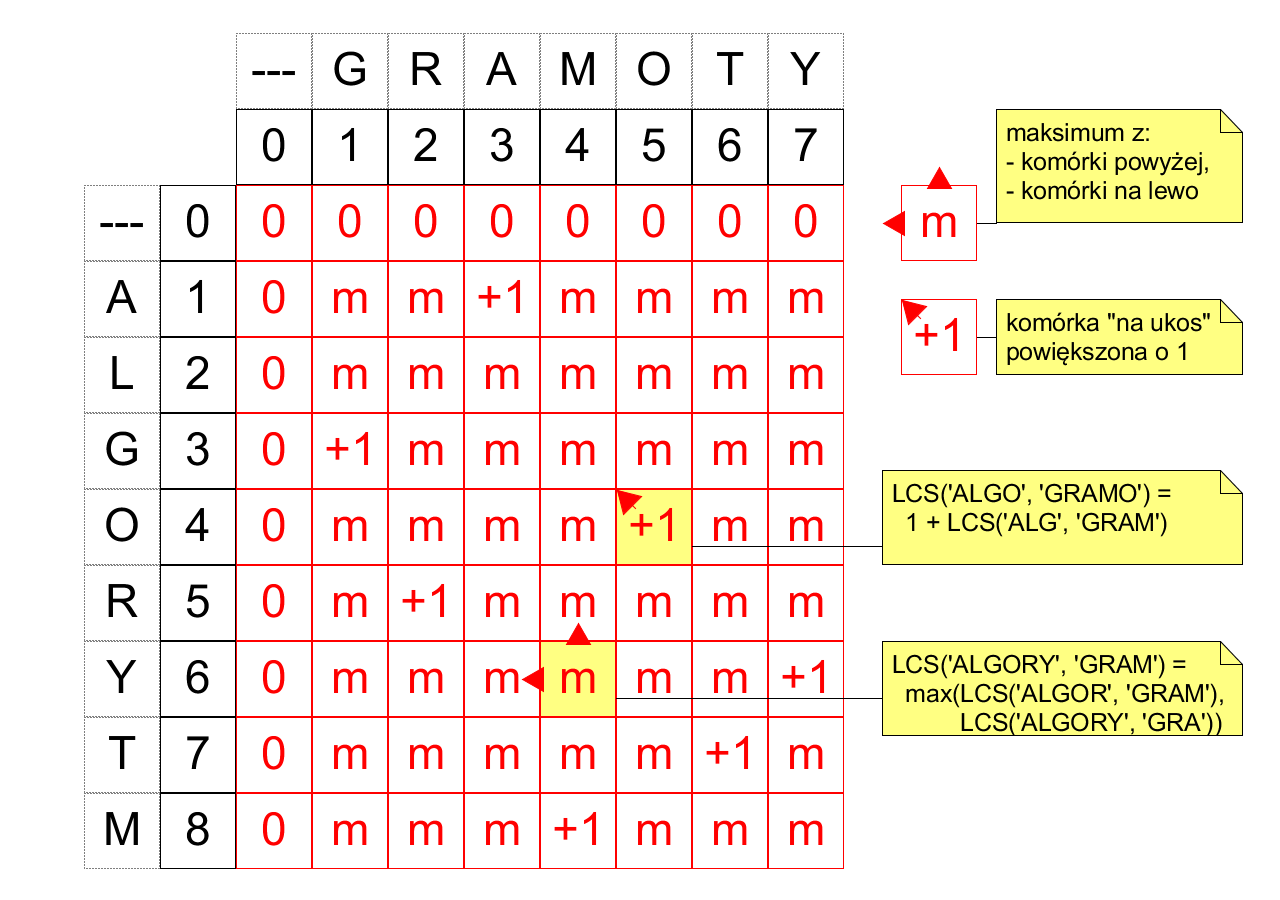
Wartość każdego współczynnika można zatem wyliczyć z użyciem jedynie współczynników na górę lub na lewo od niego. Jest to inne wyrażenie faktu, że schemat rekurencyjny opisujący $LCS$ jest poprawny. Wypełniając komórki w kolejności od pierwszego wiersza do ostatniego, od lewej kolumny do prawej, zawsze mamy wszystkie dane potrzebne do tego uzupełnienia:

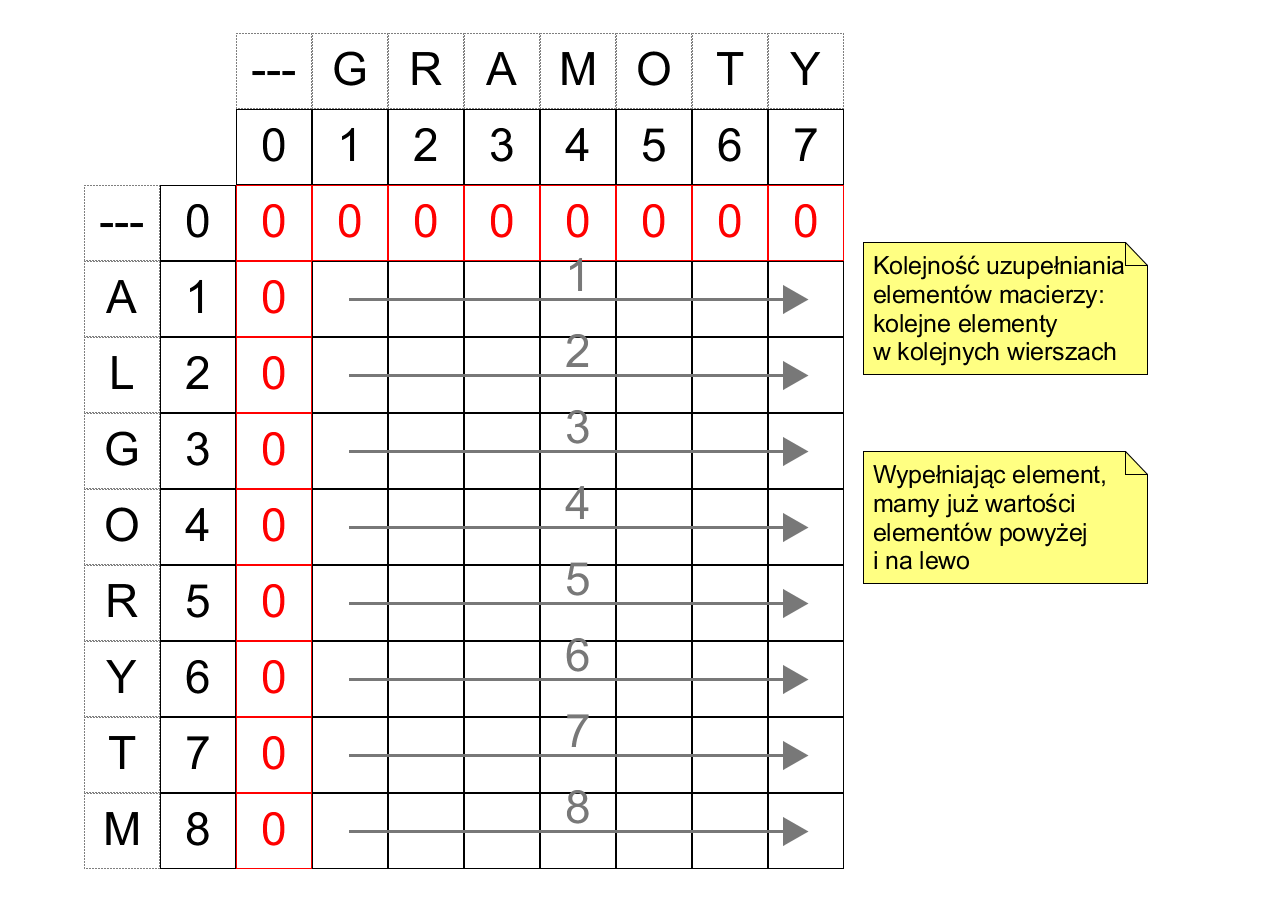
Alternatywnie, komórki można wypełniać od lewej do prawej kolumny, od góry do dołu (jest to sposób symetryczny). W ten sposób uzyskujemy:

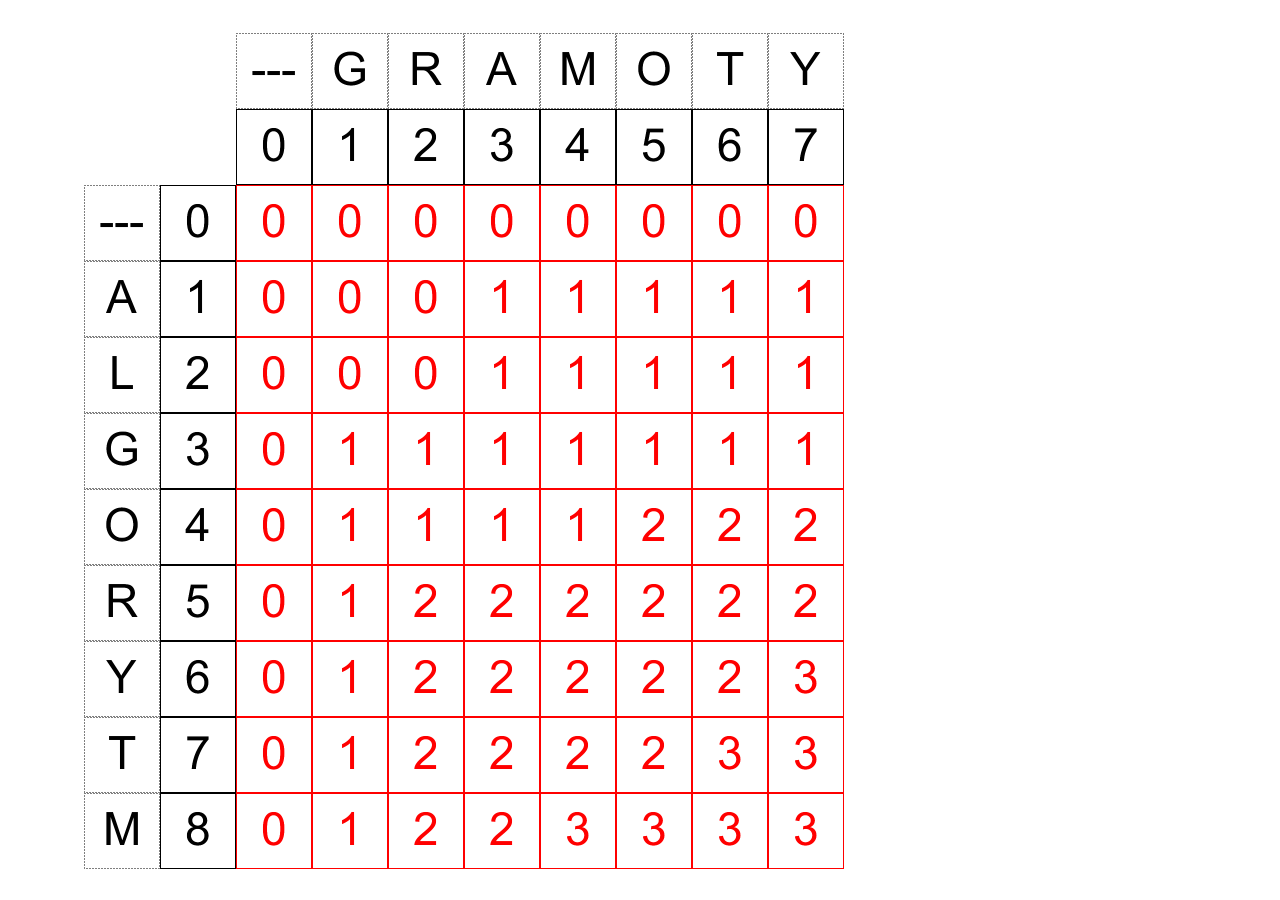
Prawy dolny współczynnik to szukana wartość $LCS$. Przykładowa implementacja tego algorytmu:

import numpy as np # dla macierzy

def lcs(a, b):
    n = len(a)
    m = len(b)
    cache = np.zeros((n + 1, m + 1), dtype=int)

    for x in range(1, n + 1):
        for y in range(1, m + 1):
            if a[x - 1] == b[y - 1]:
                cache[x, y] = 1 + cache[x - 1, y - 1]
            else:
                cache[x, y] = max(cache[x, y - 1], cache[x - 1, y])
    return cache[n, m]

print(lcs('ALGORYTM', 'GRAMOTY'))

3

Algorytm pozbawiony jest rekurencji i nietrudno zbadać, że zarówno złożoność czasowa, jak i pamięciowa to $\Theta(nm)$.

Przypomnijmy, że w problemie najdłuższego wspólnego podciągu interesuje nas nie tylko jego długość, ale konkretny przykład podciągu. Macierz uzyskana w algorytmie powyżej może posłużyć do odtworzenia takiego ciągu przez zbadanie, w jaki sposób wyznaczana jest wartość współczynnika $x_{i,j}$. Trawersujemy kolejne współczynniki macierzy, poczynając od $x_{n,m}$:

• Jeśli współczynnik jest typu "maksimum", przechodzimy do współczynnika zaświadczającego o tym maksimum. Rozwiązania (ciągi) problemów reprezentowanych przez oba współczynniki są takie same.
• Jeśli współczynnik jest typu "+1", przechodzimy do współczynnika w górę i na lewo, notując ostatni element ciągów w problemie reprezentowanym przez współczynnik. Rozwiązanie (ciąg) dla pierwszego współczynnika jest takie, jak dla drugiego, powiększone o ten element.
• Kończymy, gdy dojdziemy do zerowego wiersza lub kolumny (lub gdy wartość współczynnika to $0$).

Zanotowane w tej procedurze elementy to najdłuższy wspólny podciag w odwrotnej kolejności. Przykładowo:

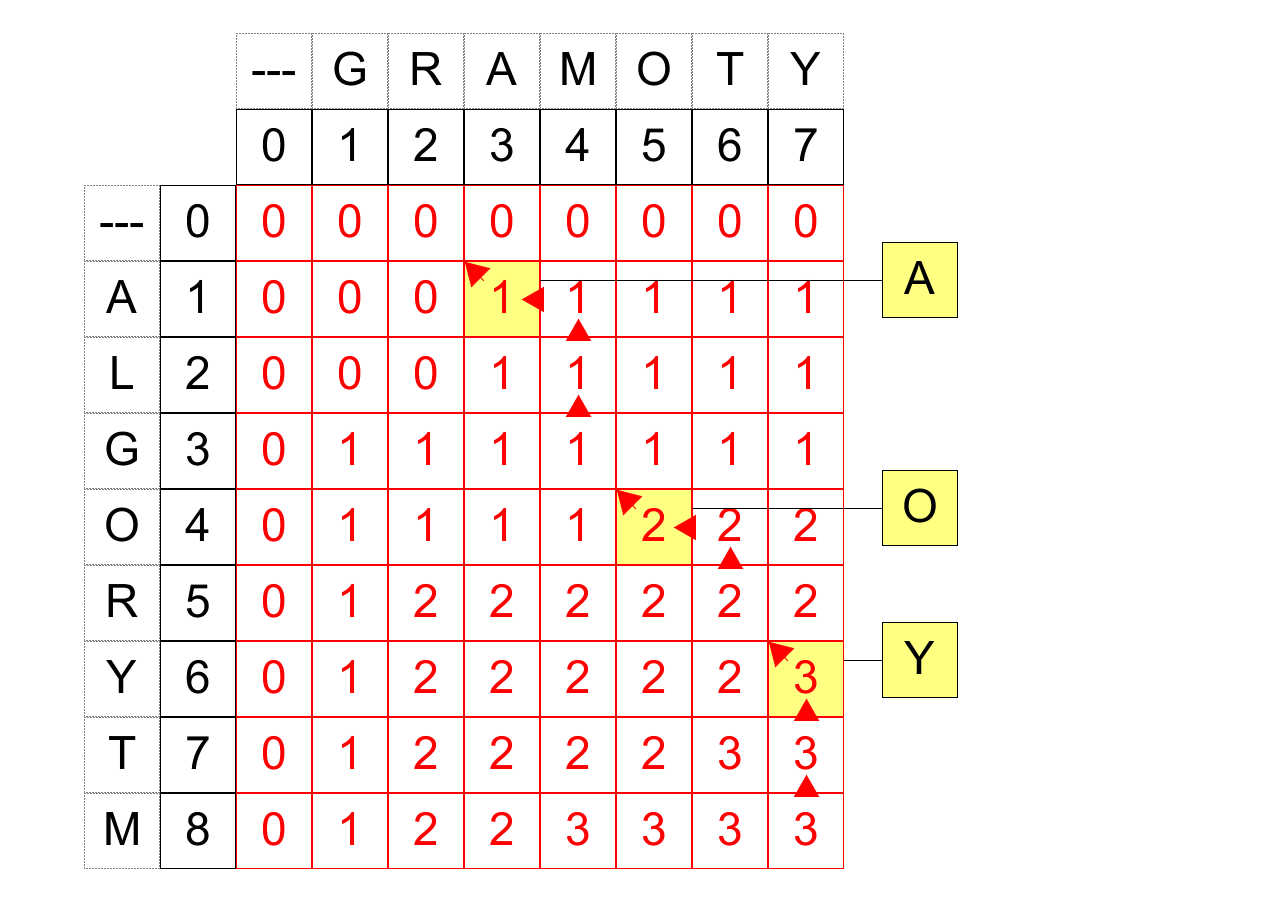
W ten sposób, metodą "od góry do dołu", rekonstruujemy rozwiązanie. Zwróćmy uwagę, że dla współczynnika typu "maksimum" często mamy wybór, do którego współczynnika przejść w następnym kroku (gdy oba realizują maksimum). W przykładzie wyżej preferujemy pójście w górę. Trawersując macierz na wszystkie sposoby zgodne z krokami wyżej dadzą nam wszystkie najdłuższe wspólne podciągi.

Uzupełnimy implementację $LCS$ o znalezienie przykładu podciągu. Uzupełnienie nie pogarsza złożoności czasowej ani pamięciowej:

def lcs(a, b):
    n = len(a)
    m = len(b)
    cache = np.zeros((n + 1, m + 1), dtype=int)

    for x in range(1, n + 1):
        for y in range(1, m + 1):
            if a[x - 1] == b[y - 1]:
                cache[x, y] = 1 + cache[x - 1, y - 1]
            else:
                cache[x, y] = max(cache[x, y - 1], cache[x - 1, y])
    result = cache[n, m]
    
    # rekonstrukcja rozwiązania:
    solution = []
    while n > 0 and m > 0:
        if a[n - 1] == b[m - 1]:
            solution.append(a[n - 1])
            n -= 1
            m -= 1
        elif cache[n, m] == cache[n - 1, m]:
            n -= 1
        else:
            m -= 1

    return result, ''.join(reversed(solution))

print(lcs('ALGORYTM', 'GRAMOTY'))

(3, 'AOY')

Programowanie dynamiczne

"Wstępujące" rozwiązanie $LCS$ to przykład tak zwanego programowania dynamicznego.

Programowanie dynamiczne to technika projektowania algorytmów rozwiązujących problemy optymalizacji, podobna do techniki "dziel i zwyciężaj". W podejściu dynamicznym, problem dzielimy na podproblemy, a następnie optymalne rozwiązanie problemu wyznaczamy przez znalezienie optymalnych rozwiązań tych podproblemów.

Problem szukania najdłuższego wspólnego podciągu jest problemem optymalizacyjnym: chcemy zmaksymalizować długość wspólnego podciągu.

Aby problem dało się rozwiązać metodą programowania dynamicznego, musi on mieć pewne własności: optymalnej podstruktury oraz wspólnych podproblemów.

I. Problem ma własność optymalnej podstruktury, gdy jego optymalne rozwiązanie jest funkcją optymalnych rozwiązań jego podproblemów. To znaczy: dla danego problemu możemy wyodrębnić pewną liczbę podproblemów, dla każdego z nich znaleźć optymalne rozwiązanie, a następnie złożyć z tych rozwiązań optymalne rozwiązanie samego problemu.

Koniecznym jest, aby rozwiązania podproblemów (użyte do rozwiązania problemu) dało się wyznaczyć niezależnie. Inaczej mówiąc: gdyby optymalne rozwiązanie głównego problemu było na przykład połączeniem optymalnych rozwiązań dwóch lub więcej podproblemów, konieczne jest, aby te optymalne rozwiązania się nie wykluczały.

Problem $LCS$ ma własność optymalnej podstruktury: podproblemy (oznaczane wcześniej $P(c, d)$) same były przykładami problemu najdłuższego wspólnego podciągu, i w każdym z przypadków optymalne rozwiązanie takiego problemu konstruowaliśmy z rozwiązania jednego z jego podproblemów. Warunek ze zdania "koniecznym jest" jest tu spełniony trywialnie: nie łączymy wielu rozwiązań podproblemów (a w jednym tylko przypadku, wybieramy jedno z dwóch rozwiązań podproblemów - to, które jest dłuższym ciągiem).

II. Problem ma własność wspólnych podproblemów, gdy wyznaczanie rozwiązań różnych podproblemów prowadzi do wyznaczania rozwiązań jeszcze mniejszych, tożsamych podproblemów.

Intuicyjnie: wszystkich podproblemów jest niewiele i w znacznym stopniu się ,,zazębiają''.

W problemie $LCS$, problemów rzeczywiście jest niewiele: wszystkich podproblemów $P(a,b)$ jest $\Theta(nm)$, gdzie $n, m$ to długości $a,b$.

Własność wspólnych podproblemów odróżnia problemy rozwiązywane "zwykłą" techniką "dziel i rządź" od tych, w których stosujemy technikę dynamiczną. Przykładowo: problem sortowania listy można (na siłę) potraktować jako problem optymalizacyjny, gdzie rozwiązaniem optymalnym jest rozwiązanie jedyne: posortowana lista wejściowa. Algorytmy sortujące oparte na metodzie "dziel i rządź" dzielą problem sortowania listy na podproblem sortowania podlist: w mergesort jest to sortowanie lewej i prawej połówki listy. Te podlisty nie mają żadnego wspólnego przekroju i w tym sensie są całkowicie niezależnymi od siebie podproblemami, które w żaden sposób się nie zazębiają.

Problem wykazujący tak opisane własności rozwiązujemy według schematu programowania dynamicznego:

1. Wyróżniamy podproblemy i charakteryzujemy optymalne rozwiązanie; wykazujemy, że problem ma własność optymalnej podstruktury.
2. Zadajemy rekurencyjne zależności między wartościami optymalnych rozwiązań podproblemów.
3. Konstruujemy wartości rozwiązań coraz większych podproblemów metodą ,,wstępną''.
4. Rekonstruujemy szczegółowe rozwiązanie problemu z wyznaczonych wartości rozwiązań podproblemów.

W tym schemacie, kroki 3. i 4. możemy zastąpić algorytmem rekurencyjnym ze "schowkiem" - techniką rekurencji ze spamiętywaniem.

W problemie $LCS$, schemat wyglądał nastepująco:

1. Podproblemy to $P(c, d)$, wartość rozwiązania oznaczamy przez $LCS(c,d)$.
2. Zadajemy zależności rekurencyjne dla funkcji $LCS$.
3. Konstruujemy "od dołu" wartości $LCS$ dla coraz dłuższych odcinków początkowych.
4. Rekonstruujemy najdłuższy wspólny podciąg, badając jak powstają wartości rozwiązań z punktu 3.

W następnym rozdziale skryptu, zastosujemy ten schemat do innych problemów: dyskretnego problemu plecakowego oraz optymalnego mnożenia ciągu macierzy.