wyklad1

Przypomnijmy za wykładem z piewszego semestru, że przez algorytm rozumiemy "zbiór precyzyjnych instrukcji wraz z regułami, w jakiej kolejności mają być wykonywane, oraz kiedy ich wykonywanie należy zakończyć". Nie utożsamiamy algorytmu z gotowym programem. Program wykonujący dany algorytm, zapisany w danym języku (np. Python), nazywamy implementacją algorytmu.

Gotowy program można uruchomić na różnych platformach. Przez platformę rozumiemy zarówno sposób, w jaki program zostaje uruchamiany (np. przez interpreter, wirtualną maszynę, lub uruchomienie skompilowanego pliku binarnego), oraz fizyczny sprzęt (procesor, etc.). Czas i pamięć potrzebna na wykonanie programu, nawet dla tych samych danych wejściowych, będzie zależeć od wielu czynników, w tym wyjdajności sprzętu, wersji interpretera; oraz szczegółów implementacji, czyli konkretnego sposobu, w jaki algorytm został przełożony na kod języka przez programistę.

Teoria złożoności obliczeniowej zajmuje się badaniem zasobów (czasu i pamięci) wykorzystwanych przez algorytm w zależności od rozmiaru danych wejściowych w sposób niezależny od implementacji. Dostarcza też narzędzi do porównywania wydajności różnych algorytmów rozwiązujących ten sam problem.

Motywujący przykład ¶

Rozważmy dwa algorytmy, które dla podanej liczby naturalnej $n$ wyznaczają sumę $0 + 1 + \ldots + n$. Oba algorytmy zapiszemy jako funkcje w Pythonie:

Algorytm A - wprost przez zsumowanie:

def sum1(n):
    total = n
    for i in range(n + 1):
        total += i
    return total

Algorytm B - przez formułę $\frac{n(n+1)}{2}$:

def sum2(n):
    return n * (n + 1) // 2

Wyznaczmy teraz czas pracy obu programów na zadanej platformie. Będziemy pracować przy pewnym założeniach:

Uwzględnimy jedynie czasy wykonywania operacji arytmetycznych. Są to operacje charakterystyczne dla algorytmów, nie samych programów$^1$.
Zakładamy, że czas wykonania pojedynczej operacji dodawania nie zależy od wielkości dodawanych liczb. Analogicznie dla pozostałych operacji arytmetycznych$^2$.
Rozróżniamy jednak (na razie) czasy potrzebne na wykonanie różnych operacji arytmetycznych$^3$.

$^1$ Nie są to wszystkie operacje w programach: na potrzeby implementacji (np. kontroli przepływu sterowania), w programach występują też np. przypisanie i tworzenie obiektu `range`; samo iterowanie po tym obiekcie też nie jest "darmowe".
$^2$ Założenie o stałym czasie operacji arytmetycznych będzie funkcjonować przez większość kursu, aż zostanie ujawniona prawda.
$^3$ W praktyce mnożenie bywa bardziej czasochłonne od dodawania, a dzielenie jeszcze bardziej.

Oznaczmy przez $t_a, t_m$ i $t_d$ czasy wykonywania dodawania, mnożenia i dzielenia odpowiednio. Czasy te możemy wyrazić w dowolnej jednostce, np. nanosekundach, cyklach procesora etc. Naturalnie zakładamy, że czasy te są dodatnie. Wtedy czasy wykonania obu funkcji możemy wyrazić jako:

A) $n \cdot t_a$,

B) $t_a + t_m + t_d$.

Czasy $t_a, t_m, t_d$ są zależne od platformy i mogą znacząco się różnić, nawet na procesorach podobnej generacji. Często zależą też od języka, w którym algorytm został zaimplementowany (dodawanie liczb w Pythonie "na surowo" jest wolniejsze, niż np. w C). Proporcje czasów różnych operacji też nie są stałe. O ile więc można mówić o czasie działania programu na konkretnej platformie, nie mamy jeszcze sposobu na obiektywną ocenę samych algorytmów.

Zauważmy jednak, że niezależnie od wartości stałych $t_a, t_m, t_d$ funkcja opisująca czas działania programu realizującego A jest rosnącą do nieskończoności funkcją liniową, a analogiczna funkcja dla programu realizującego B jest stała. Nawet jeśli dla małych $n$ pierwszy program będzie działał szybciej, to dla dostatecznie dużych $n$ będzie już działał wolniej. Co więcej, proporcja czasu działania pierwszego programu do czasu działania drugiego rośnie do nieskończoności.

Powyższa własność nie jest już cechą samych implementacji, a wynika z samych algorytmów. Przy poczynionych wcześniej założeniach, jesteśmy uprawnieni do postawienia następujących tez:

Każda implementacja A działa w czasie liniowo zależnym od $n$.
Każda implementacja B działa w stałym czasie.
Stąd, dla dowolnych dwóch implementacji A i B, dla dostatecznie dużych $n$ ta druga implementacja będzie wydajniejsza (szybsza).

Teoria złożoności obliczeniowej uogólnia poczynioną wyżej analizę do dowolnych algorytmów. Staramy się w niej abstrahować od szczegółów implementacji i czasów działania konkretnych implementacji, a koncentrujemy się na opisie asymptotycznego zachowania takich czasów (czyli zachowania funkcji, gdy jej argument - rozmiar danych - rośnie do nieskończoności). Jeśli czas działania implementacji jest opisany funkcją liniową, wynika to z natury algorytmu. Konkretne nachylenie takiej funkcji liniowej jest już czymś przypadkowym i wynika z czasów konkretnych operacji na danej platformie.

Hasło przewodnie - "ignorujemy stałe" (konkretne czasy operacji).

Intuicja z analizy ¶

Przed przejściem do formalizmu związanego ze złożonością obliczeniową, przywołamy pewne intuicje ze świata analizy. Rozważmy trzy funkcje rzeczywiste:

$x$,

$x^2$,

$\frac{x}{2} + 1$.

Rozważmy ich zachowanie asymptotyczne, czyli co się dzieje, gdy $x$ dąży do nieskończoności. Każda z funkcji rośnie do nieskończoności, ale, intuicyjnie, niekoniecznie rosną tak samo szybko.

Mamy $\lim_{x \to \infty} \frac{x^2}{x} = \infty$, co pozwala powiedzieć, że funkcja $x^2$ rośnie szybciej, niż $x$, i analogicznie dla $\frac{x}{2} + 1$.
Inaczej wygląda kwestia porównania $x$ i $\frac{x}{2} + 1$. W pewnym sensie, $x$ rośnie szybciej: "mniej więcej" dwa razy.
Z drugiej strony, badając proporcje tych funkcji mamy $\lim_{x \to \infty} \frac{x}{\frac{x}{2} + 1} = 2 > 0$, a zatem z dokładnością do $\varepsilon$ ta proporcja jest stała i dodatnia.

Zaniedbując konkretną wartość tej proporcji, można przyjąć, że $x$ i $\frac{x}{2} + 1$ rosną "tak samo" szybko. Można wtedy to stwierdzenie rozciągnąć na wszystkie (rosnące) funkcje liniowe.

Notacja asymptotyczna ¶

Wprowadzimy teraz notację matematyczną zwaną notacją wielkiego $O$ (big $O$ notation, notacja Landaua), służącą do klasyfikowania asymptotycznego zachowania funkcji, oraz powiązane z nią notacje $\Omega$ i $\Theta$. Notację tę stosuje się w różnych kontekstach (nie tylko w złożoności obliczeniowej).

Uwaga. W literaturze można znaleźć różne sposoby definiowania notacji asymptotycznej oraz różne stosowane wraz z nią konwencje.

Zbiory $O(\cdot), \Omega(\cdot)$ i $\Theta(\cdot)$¶

W dalszej części rozdziału rozważamy funkcje ze zbioru $\mathbb{N}$ w zbiór nieujemnych liczb rzeczywistych, czyli elementy zbioru $\mathbb{R}_{\geq 0}^\mathbb{N}$. Dla funkcji $f \in \mathbb{R}_{\geq 0}^\mathbb{N}$ definiujemy następujący podzbiór $\mathbb{R}_{\geq 0}^\mathbb{N}$: $$O(f) = \{g \in \mathbb{R}_{\geq 0}^\mathbb{N} : \exists_{M > 0} ~ \exists_{n_0 \in \mathbb{N}} ~ \forall_{n \geq n_0} ~ g(n) \leq M \cdot f(n)\}.$$

Fragment ,,$\exists_{n_0 \in \mathbb{N}} ~ \forall_{n \geq n_0} \ldots$'' to znane z analizy "dla dostatecznie dużych $n$ $\ldots$".

Funkcja $g$ jest więc elementem $O(f)$, jeśli istnieje stała $M > 0$ taka, że dla dostatecznie dużych $n$ zachodzi $g(n) \leq M \cdot f(n)$. Bardziej opisowo: $g(n)$ da się ograniczyć z góry przez pewne przeskalowanie $f(n)$ przez stałą (dodatnie $M$ spod kwantyfikatora), być może poza małymi $n$.

Gdy $g \in O(f)$, powiemy że $g$ rośnie (asymptotycznie) nie szybciej niż $f$ - przy czym nie wiemy jeszcze, czy takie określenie będzie miało sens.

Przykład. Rozważmy funkcje $f(n) = 2n, g(n) = 100n, h(n) = n^2$. Mamy:

$f \in O(g)$, bo $2n \leq 100n$ dla dostatecznie dużych $n$ (a nawet wszystkich).

$g \in O(f)$, bo $100n \leq 50 \cdot 2n$ dla wszystkich $n$.

$f \in O(h)$, bo $n \leq n^2$ dla wszystkich $n$

$g \in O(h)$, bo $100n \leq n^2$ dla wszystkich $n$ większych od $99$.

$h \notin O(f)$, bo dla dowolnej $M$, nierówność $n^2 \leq M \cdot 2n$ zachodzi tylko dla skończenie wielu $n$.

W ramach konwencji, możemy pisać $g(n) \in O(f(n))$ w znaczeniu $g \in O(f)$, czyli wyeksponować parametr funkcji. Możemy też zastąpić obie funkcje wyrażeniami, które je opisują; w szczególności możemy napisać:

$n \in O(n)$,
$\frac{n}{2} \in O(n)$,
$100n \in O(2n)$,
$n \in O(n^2)$,
$n^2 + n + 1 \in O(n^2)$,
$100 \in O(1)$.

Wszystkie powyższe należenia są prawdziwe.

Analogicznie dla $f \in \mathbb{R}_{\geq 0}^\mathbb{N}$ definiujemy: $$\Omega(f) = \{g \in \mathbb{R}_{\geq 0}^\mathbb{N} : \exists_{m>0} ~ \exists_{n_0 \in \mathbb{N}} ~ \forall_{n \geq n_0} ~ m \cdot f(n) \leq g(n)\}.$$

Zbiór $\Omega(f)$ składa się z tych funkcji, które są ograniczone z dołu przez pewne przeskalowanie $f$ (przez stałą $m > 0$), być może poza małymi $n$. Gdy $g \in \Omega(f)$, powiemy, że $g$ rośnie (asymptotycznie) nie wolniej niż $f$.

Wreszcie definiujemy: $$\Theta(f) = O(f) \cap \Omega(f).$$ Funkcja $g$ należy fo $\Theta(f)$ gdy można ją jednocześnie ograniczyć z dołu i z góry przez pewne przeskalowania $f$ (z wyjątkiem małych $n$).

Możemy też zdefiniować $\Theta(f)$ jako zbiór $$\{g \in \mathbb{R}_{\geq 0}^\mathbb{N} : \exists_{m,M>0} ~ \exists_{n_0 \in \mathbb{N}} ~ \forall_{n \geq n_0} ~ m \cdot f(n) \leq g(n) \leq M \cdot f(n)\}.$$

Z definicji wynika już, że gdy $g \in \Theta(f)$, to mówimy, że $g$ rośnie nie wolniej i nie szybciej, niż $f$. W tej sytuacji powiemy po prostu, że $g$ rośnie tak samo szybko, jak $f$.

W notacjach $\Omega$ i $\Theta$ stosujemy te same konwencje, co dla $O$, zatem możemy napisać:

$n + 1 \in \Theta(2n)$,
$n^2 \in \Omega(n)$.

W następnym podrozdziale pokażemy, że kolokwializm "funkcja $g$ rośnie nie wolniej/nie szybciej/tak samo szybko, jak $f$" jest uprawniony.

Relacja wspólnego tempa wzrostu i porządek na klasach ¶

Przypomnienie z wykładu Wstęp do matematyki: relacja $R$ na zbiorze $X$ jest:

Zwrotna, gdy $xRx$ dla wszystkich $x \in X$.
Symetryczna, gdy $xRy \iff yRx$ dla wszystkich $x, y \in X$.
Przechodnia, gdy $xRy \land yRz \Rightarrow xRz$ dla wszystkich $x, y, z \in X$.
Słabo antysymetryczna, gdy $xRy \land yRx \Rightarrow x = y$ dla wszystkich $x, y \in X$.

Relacja jest relacją równoważności gdy jest zwrotna, symetryczna i przechodnia. Relacja taka dzieli (partycjonuje) zbiór $X$ na klasy abstrakcji złożone z elementów parami równoważnych. Zbiór tych klas nazywamy zbiorem ilorazowym (relacji $R$). Relacja jest porządkiem częściowym, gdy jest zwrotna, przechodnia i słabo antysymetryczna.

Każda funkcja $f \in \mathbb{R}_{\geq 0}^\mathbb{N}$ wyznacza zbiór $\Theta(f) \subset \mathbb{R}_{\geq 0}^\mathbb{N}$. Pokażemy teraz, że zbiory tej postaci są klasami pewnej relacji równoważności, którą zinterpretujemy jako relację "wspólnego tempa wzrostu".

Definicja. Określmy relację $\sim$ na $\mathbb{R}_{\geq 0}^\mathbb{N}$ przez $$f \sim g \iff f \in \Theta(g).$$

Zauważmy następujące:

Fakt 1. Dla $f, g \in \mathbb{R}_{\geq 0}^\mathbb{N}$ mamy $$g \in O(f) \iff f \in \Omega(g).$$ Dowód. Z definicji, $g \in O(f)$ oznacza, że dla pewnej stałej $M$ mamy $g(n) \leq M \cdot f(n)$ dla dostatecznie dużych $n$. Równoważnie, $\frac{1}{M}g(n) \leq f(n)$ (dla dostatecznie dużych $n$), czyli $f$ jest ograniczona z dołu przez pewne przeskalowanie $g$ (przez stałą $m = \frac{1}{M}$) dla dostatecznie dużych $n$. To dokładnie oznacza, że $f \in \Omega(g)$. Implikacja w drugą stronę jest analogiczna.

Kolokwialnie, fakt wyraża równoważność stwierdzeń: $g$ rośnie nie szybciej niż $f$ wtedy i tylko wtedy, gdy $f$ rośnie nie wolniej niż $g$.

Uwaga. W niektórych podręcznikach, treść powyższego faktu jest użyta do zdefiniowania $\Omega(\cdot)$ przy pomocy $O(\cdot)$, zamiast definicji ze stałą $m$.

Możemy teraz udowodnić zapowiedziany fakt o relacji $\sim$:

Stwierdzenie 2. Relacja $\sim$ jest relacją równoważności.
Dowód. Zwrotność: dla wszystkich $f$ mamy $f \in \Theta(f)$ , bo $f$ ogranicza samą siebie i z góry, i z dołu, czyli $f \sim f$.
Symetryczność: Niech $f \sim g$, czyli $f \in \Theta(g)$. Z definicji mamy więc $f \in O(g)$ oraz $f \in \Omega(g)$. Z Faktu 1 te należenia są równoważne odpowiednio $g \in \Omega(f)$ i $g \in O(f)$, a te warunki z kolei oznaczają, że $g \in \Theta(f)$. Zatem $g \sim f$.
Przechodniość: Niech $f \sim g$ i $g \sim h$. Mamy stałe $m_1, M_1$ takie, że dla dostatecznie dużych $n$: $$m_1 g(n) \leq f(n) \leq M_1 g(n),$$ oraz stałe $m_2, M_2$ takie, że dla dostatecznie dużych $n$: $$m_2 h(n) \leq g(n) \leq M_2 h(n).$$ Dla dostatecznie dużych $n$ mamy więc: $$(m_1 m_2) h(n) \leq f(n) \leq (M_1 M_2) h(n),$$ czyli $f \in \Theta(h)$, a więc $f \sim h$.

Bezpośrednio z definicji $\sim$ mamy też:

Fakt. $[f]_{\sim} = \Theta(f)$ (gdzie $[f]_{\sim}$ oznacza klasę abstrakcji $f$).

Przyjrzyjmy się kilku przykładom klas relacji $\sim$:

$\Theta(1)$ - zawiera wszystkie dodatnie funkcje stałe.
$\Theta(n)$ - zawiera wszystkie rosnące funkcje liniowe.
$\Theta(n^k)$ - zawiera wszystkie (nieujemne) wielomiany stopnia dokładnie $k$.
$\Theta(\log n)$ - zawiera wszystkie logarytmy (przyjmujemy konwencję, że $\log0 = 0$).

Zwracamy jednak uwagę, że powyższe klasy zawierają też inne funkcje. Przykładowo, mamy $10 + \sin(n) \in \Theta(1)$. Podobnie, $n + \log n \in \Theta(n)$.

Przynależenie funkcji do danej klasy pozwala mówić o sposobie, w jaki ta funkcja rośnie: na przykład, funkcje z $\Theta(n)$ "rosną liniowo", funkcje z $\Theta(n^2)$ "rosną kwadratowo" (nawet jeśli nie są wielomianami drugiego stopnia). Funkcje z $\Theta(\log n)$ "rosną logarytmicznie". O funkcjach z $\Theta(1)$ mówimy po prostu, że są "stałe" (jest to drobne nadużycie).

Na koniec podrozdziału uzasadnimy wreszcie zasadność określeń typu "funkcja maleje nie wolniej niż druga" przez formalne wprowadzenie na klasach $\Theta(\cdot)$ częściowego porządku.

Definicja. Na zbiorze ilorazowym $\big(\mathbb{R}_{\geq 0}^\mathbb{N}\big)_{/\sim}$ wprowadzamy relację: $$\Theta(f) \leq \Theta(g) \iff f \in O(g).$$

Fakt. Relacja $\leq$ jest dobrze zdefiniowana: jeśli $\Theta(f) = \Theta(f')$ to $f \in O(g) \iff f' \in O(g)$, (czyli relacja między $\Theta(f)$ i $\Theta(g)$ nie zależy od tego, którą funkcję z $\Theta(f)$ wybierzemy do sprawdzenia, czy relacja zachodzi) i jest relacją częściowego porządku.
Dowód. Ćwiczenie.

Standardowo, z porządku nieostrego $\leq$ definiujemy porządek ostry $<$ pisząc $\Theta(f) < \Theta(g)$ w znaczeniu $\Theta(f) \leq \Theta(g) \land \Theta(f) \neq \Theta(g)$.

Przy użyciu porządku na klasach, możemy w formalny sposób wyrazić analityczne intuicje dotyczące porównania tempa wzrostu funkcji. Na przykład mamy: $$\Theta(1) < \Theta(n) < \Theta(n^2).$$ Kolokwialnie te nierówności znaczą, że funkcje stałe rosną wolniej niż funkcje liniowe, a funkcje liniowe rosną wolniej niż kwadratowe. Bardziej ściśle należałoby powiedzieć, funkcje rosnące tak samo szybko jak funkcje stałe rosną wolniej niż liniowo, a z kolei funkcje które rosną liniowo rosną wolniej niż kwadratowo.

Opisywanie złożoności algorytmów ¶

Wprowadzoną wcześniej notacją asymptotyczną możemy opisywać czasy działania algorytmów w następujący sposób:

Opisujemy czas działania algorytmu jako funkcję $T(n)$, gdzie $n$ jest rozmiarem danych
Badamy asymptotyczne zachowanie funkcji $T$ przez opis jej klasy $\Theta(T)$.
Porównujemy tak wyznaczoną klasę z klasami innych algorytmów.

Jeśli wyznaczenie klasy $\Theta(T)$ jest trudne, możemy próbować znaleźć mniej dokładne ograniczenia wzrostu $T$, na przykład przez podanie $f$, $g$ takich, że $T \in O(f)$ i $T \in \Omega(g)$.

Porównanie klas dwóch algorytmów pozwala nam na porównanie ich wydajności w podobny sposób, jak dla algorytmów A i B z przykładu z początku rozdziału. Jeśli $T_1$ i $T_2$ są czasami działania algorytmów $A_1$ i $A_2$ odpowiednio, i $\Theta(T_1) < \Theta(T_2)$, to algorytm $A_1$ jest wydajniejszy niż $A_2$ - przynajmniej dla dostatecznie dużych danych.

W powyższym "przepisie" pojawia się kilka niedoprecyzowanych pojęć:

Co to jest "rozmiar danych"?
Czym jest "czas działania algorytmu" i w jaki sposób go wyznaczać?

Każdy algorytm działa na pewnym rodzaju danych wejściowych. Takim "wejściem" mogą być dowolne obiekty lub kolekcje obiektów: pojedyncza liczba, ale też lista, plik, etc. Rozmiar danych to cecha, którą przypisujemy każdej danej wejściowej. Czas działania algorytmu będziemy wyznaczać względem tej cechy. Na razie, taką cechą będzie dla nas pojedyncza liczba naturalna. Posłużmy się przykładami:

Przykład 1. Daną algorytmu A liczącego $0 + 1 + \ldots + n$ jest pojedyncza liczba $n$. Możemy po prostu przyjąć jej wartość jako rozmiar danych. Wtedy czas działania algorytmu (licząc wyłącznie operacje arytmetyczne) $T(n)$ wyraża się jako $T(n) = t_a \cdot n \in \Theta(n)$, zatem powiemy, że czas działania algorytmu jest liniowy w zależności od $n$ (należy do $\Theta(n)$, albo jest klasy $\Theta(n)$).

Przykład 2. Dla algorytmu B i rozmiaru danych określonego jak dla A, jego czas działania jest stały ($T(n) = t_a + t_m + t_d$), czyli jest w $\Theta(1)$.

W powyższych przykładach sytuacja była jasna - dane są tożsame z ich rozmiarem. Rozważmy jednak inny algorytm, którego wejściem jest lista parami porównywalnych obiektów (na przykład liczb).

Przykład 3. Algorytm znajdujący największy element listy (znów zapisany w Pythonie):
def maximum(lst):
    if len(lst) == 0: raise ValueError
    m = lst[0]
    for element in lst:
        if element > m:
            m = element
    return m
Kluczową operacją w tym algorytmie jest porównywanie obiektów z listy. Porównań tych będzie tyle, ile elementów na liście. Zatem możemy przyjąć jej długość za roamiar danych ($n$ = len(lst)), a wtedy czas działania algorytmu (zliczając tylko porównania) w zależności od $n$ jest klasy $\Theta(n)$. Inaczej mówiąc, algorytm działa liniowo względem długości listy.

Operacje elementarne ¶

W podanych przykładach nie jest do końca jasne, dlaczego zliczamy takie a nie inne operacje w prezentowanych kodach. Szersze wyjaśnienie pojawi się w następnym rozdziale skryptu. Na razie ograniczymy się tylko do stwierdzenia, że zliczamy niektóre tak zwane operacje elementarne, między innymi operacje arytmetyczne, porównania, przypisania.

O czasach takich operacji elementarnych zakładamy, że są stałe. Co więcej, będziemy zakładać, że wszystkie wykonują się w stałym czasie równym $1$. Nie wpłynie to na analizę czasu działania dokonaną przy pomocy notacji $O$. Nie uzasadnimy poprawności tego założenia formalnie, ale posłużymy się przykładem.

Przykład. Dla pewnego algorytmu przypuśćmy, że dla danych rozmiaru $n$ wykonuje on $n^2$ mnożeń, $2n^2 + n$ dodawań i $n + 10$ dzieleń. Po implementacji tego algorytmu i oznaczeniu czasów operacji jak na początku rozdziału, czas wykonania dla danych rozmiaru $n$ opisze się funkcją $$T(n) = (t_m + 2 t_a)n^2 + (t_a + t_d)n + 10 t_d.$$ Funkcja ta jest wielomianem stopnia $2$, a więc jest w klasie $\Theta(n^2)$ niezależnie od wartości stałych. Zatem bez straty ogólności możemy założyć $t_a = t_d = t_m = 1$.

Czas pesymistyczny, optymistyczny i średni ¶

Określiliśmy już pojęcie rozmiaru danych i w przybliżeniu powiedzieliśmy, jak wyznaczać czas działania danego algorytmu. Zwróćmy jednak uwagę, że rozmiar danych może nie być wystarczającą informacją do określenia liczby operacji wykonanych dla danych tego rozmiaru. Przykładowo, jeśli daną dla algorytmu jest lista (której długość jest rozmiarem danych), to dla różnych list tej samej długości algorytm może działać inaczej i wykonywać mniej lub więcej operacji. Istnieją dwa rozwiązania problemu:

Inaczej zdefiniować rozmiar danych, lub
Podzielić dane na przypadki.

Zilustrujemy problem na kolejnym przykładzie:

Przykład 4. Algorytm (jak zawsze, jako kod w Pythonie) przyjmuje listę lst długości $n$ złożoną z liczb $0, 1, 2, \ldots, n-1$ (każda występuje w lst dokładnie raz) i szuka indeksu pierwszej "transpozycji", czyli pary kolejnych liczb z listy, które nie są uporządkowane:
def find_transposition(lst):
    n = len(lst)
    for i in range(0, n - 1):
        if lst[i] > lst[i + 1]:
            return i
    return None
O liście lst możemy myśleć jako permutacji zbioru $\{0, 1, 2, \ldots, n-1\}$. Wszystkich list długości $n$, dla których przeznaczony jest algorytm jest zatem $n!$.

Przypuśćmy teraz, że analizujemy algorytm licząc tylko operacje porównania. Jeśli rozmiarem danych $n$ jest długość listy, nie możemy jednoznacznie określić ile takich porównań się wykona:

Jeśli lista jest na przykład postaci [1, 0, ...], wtedy wykona się tylko jedno porównanie (niezależnie od długości listy).

Jeśli lista jest posortowana, wtedy wykona się maksymalna liczba porównań: $n-1$.

Dla "przypadkowej" listy: trudno powiedzieć: między $0$ a $n-1$ ($0$ tylko dla $n < 2$).

Powyższe listy reprezentują trzy możliwe przypadki danych tego samego rozmiaru: najlepszy (gdy potrzeba najmniej operacji), najgorszy (gdy potrzeba ich najwięcej), oraz "średni". Możemy użyć tych przypadków do dookreślenia czasu działania algorytmu.

Definicja. Niech będzie dany algorytm wraz z ustalonym pojęciem "rozmiaru danych" (gdzie dla jednego rozmiaru istnieje wiele danych tego rozmiaru). Dla konkretnej danej wejściowej $\delta$, niech $T(\delta)$ oznacza czas działania algorytmu dla $\delta$. Niech $\Delta_n$ oznacza zbiór wszystkich danych wejściowych rozmiaru $n$. Zakładamy na razie, że $\Delta_n$ jest skończony. Definiujemy:

Optymistyczny czas działania algorytmu: $$T_{\text{best}}(n) := \min_{\delta \in \Delta_n} T(\delta).$$

Pesymistyczny czas działania algorytmu: $$T_{\text{worst}}(n) := \max_{\delta \in \Delta_n} T(\delta).$$

Średni czas działania algorytmu: $$T_{\text{avg}}(n) := \frac{1}{|\Delta_n|} \sum_{\delta \in \Delta_n} T(\delta).$$

Słownie: czas optymistyczny definiujemy w ten sposób, że dla każdego rozmiaru danych $n$ wybieramy taką daną $\delta$ rozmiaru $n$, dla której algorytm wykona najmniej operacji. Przyjmujemy liczbę tych operacji za $T_{\text{best}}(n)$. Inaczej mówiąc, analizujemy algorytm tak, jak gdyby zawsze dostawał "najlepsze" dane. Analogicznie dla czasu pesymistycznego, gdzie zakładamy, że dane zawsze są "najgorsze". Średni czas to uśredniony czas działania dla wszystkich danych danego rozmiaru.

Kluczowa obserwacja: $T_{\text{best}}(n), T_{\text{worst}}(n)$ i $T_{\text{avg}}(n)$ są konkretnymi, ustalonymi funkcjami z $\mathbb{R}_{\geq 0}^\mathbb{N}$, więc możemy rozważać ich wzrost z użyciem notacji asymptotycznej.

Dla algorytmu z Przykładu 4, danymi rozmiaru $n$ są permutacje długości $n$. Dla każdego $n$ istnieje permutacja, dla której algorytm wykona jedno porównanie. Stąd $T_{\text{best}}(n) \in \Theta(1)$. Istnieje też permutacja, dla której zostanie wykonane $n-1$ operacji (najwięcej, ile może się wykonać), zatem $T_{\text{worst}}(n) \in \Theta(n)$. Przypadek średni jest bardziej zajmujący. Mamy $\Delta_n = S_n = S_{\{0,1,\ldots,n\}}$, więc: $$T_{\text{avg}}(n) := \frac{1}{n!} \sum_{\sigma \in S_n} T(\sigma).$$

Na pierwszy rzut oka, nie jest łatwo określić, jakiej klasy jest $T_{\text{avg}}$ (wyjąwszy tautologiczne stwierdzenie, że $T_{\text{avg}} \in \Theta(T_{\text{avg}})$). Analiza optymistycznego i pesymistycznego przypadku pozwala nam ograniczyć taką średnią z góry i z dołu: $$1 \leq T_{\text{avg}}(n) \leq n - 1,$$ skąd dostajemy $T_{\text{avg}}(n) \in \Omega(1)$ oraz $T_{\text{avg}}(n) \in \Omega(n)$. Może się zdarzyć, że takie częściowe oszacowania na wzrost funkcji to najlepsze, co o danej funkcji da się powiedzieć. Ulepszymy te oszacowania później.

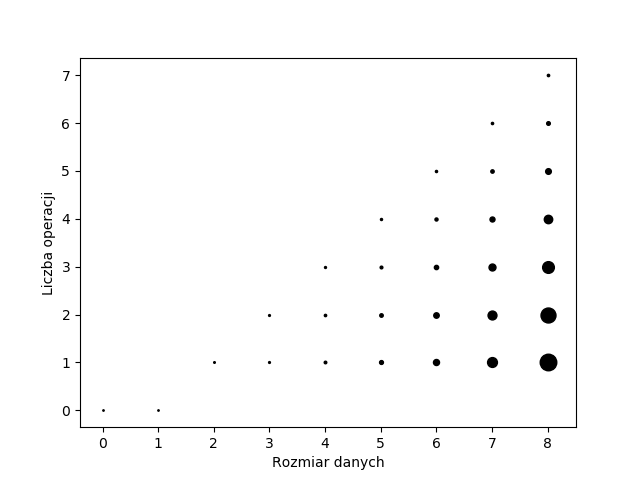
Zróbmy ilustrację, która posłuży nam do zobrazowania zdefiniowanych czasów. Wykres poniżej tworzymy w następujący sposób. Na osi $OX$ znajdują się rozmiary danych, zaś na osi $OY$ czasy działania (liczby wykonanych operacji). Dla każdego $n$ z osi $OX$ rozważamy wszystkie $n!$ permutacji rozmiaru $n$. Dla każdej takie permutacji $\sigma$ wyznaczamy czas działania algorytmu $T(\sigma)$ z przykładu i stawiamy kropkę w punkcie $\big(n, T(\sigma)\big)$. Nad każdym $n$ stawiamy zatem $n!$ kropek. Ponieważ $T(\sigma) \in \{0, 1, \ldots, n-1\}$, dla wielu permutacji rozmiaru $n$ wartość $T$ będzie taka sama, zatem zaznaczamy na wykresie ile kropek postawiliśmy w danym punkcie:

Liczba kropek w punkcie jest proporcjonalna do pola zaznaczonej kropki. Widzimy, że dla wszystkich $n \leq 8$, permutacji rozmiaru $n$ dla których czas działania wynosi $n - 1$ jest najmniej. Im mniej operacji, tym więcej jest permutacji, które tylu operacji wymagają. Permutacje wymagające tylko jednego porównania dominują.

Następnie na wykresie zaznaczamy funkcje opisujące czasy najlepsze, najgorsze i średnie. Wykonujemy to łącząc kropki rosnące najwyżej dla każdeo rozmiaru danych (dla czasu pesymistycznego) i najniżej (dla czasu optymistycznego). Czas uśredniony to średnia wyliczona "po kropkach". Otrzymujemy:

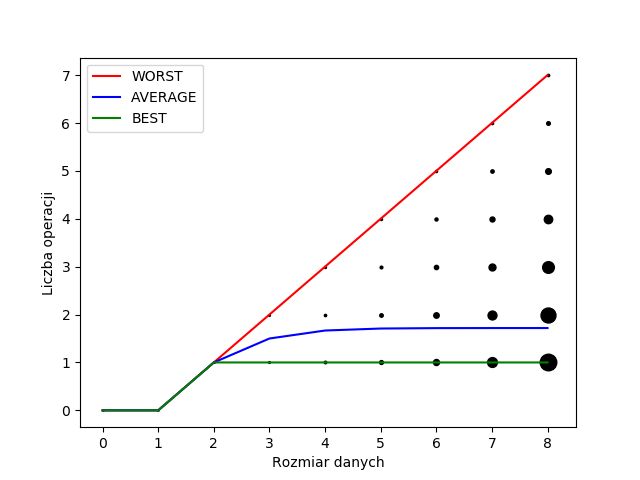
Wykres sugeruje, ze $T_{\text{avg}}(n)$ rośnie bardzo wolno, lub wręcz jest stała. Rzeczywiście (co może być trudne do pokazania), mamy $$\lim_{n \to \infty} \frac{1}{n!} \sum_{\sigma \in S_n} T(\sigma) = e - 1,$$ czyli dla dostatecznie dużych $n$, $1 < T_{\text{avg}}(n) < 2$, zatem $T_{\text{avg}} \in \Theta(1)$.

Uwaga. Poniższy materiał wymaga podstaw teorii miary, rachunku prawdopodobieństwa, lub statystyki. Należy go traktować jako uzupełniający.

Poczyniliśmy założenie, że $\Delta_n$ jest skończony, i czas średni dla danych rozmiaru $n$ był zwykłą średnią czasów z $\Delta_n$. To podejście ma dwie wady:

Zbiór danych nie zawsze jest skończony, przynajmniej w matematycznym sensie (na przykład listy liczb rzeczywistych rozmiaru $n$).
W praktyce, nie wszystkie dane pojawiają się z jednakowym prawdopodobieństwem, a średnia arytmetyczna przyznaje każdej taką samą wagę.

Oba problemy można rozwiązać w jeden sposób: określamy na $\Delta_n$ miarę probabilistyczną $\mu$, opisującą prawdopodobieństwo otrzymania danych, oraz zastępujemy prawdopodobieństwo analogiczną całką z tak określoną miarą: $$T_{\text{avg}}(n) = \int_{\Delta_n} T(\delta)d\mu.$$ Szczególnym przypadkiem jest (znormalizowana) miara licząca na zbiorze skończonym, która prowadzi do średniej arytmetycznej.

Wykład 1: złożoność obliczeniowa¶

Spis treści¶

Teoria złożoności obliczeniowej ¶