1. ![]() . Definiujemy
. Definiujemy
![]() .
. ![]() ma więc
długość
ma więc
długość ![]() .
.
2. Załóżmy, że ![]() i zdefiniowaliśmy już wektory
i zdefiniowaliśmy już wektory
![]() tworzące bazę ortonormalną podprzestrzeni
tworzące bazę ortonormalną podprzestrzeni ![]() . Znajdziemy
wektor
. Znajdziemy
wektor ![]() taki, że wektory
taki, że wektory
![]() są bazą
ortonormalną przestrzeni
są bazą
ortonormalną przestrzeni ![]() .
.
Niech

Na mocy uwagi 10.9, wektor ![]() jest ortogonalny do
jest ortogonalny do ![]() ,
więc wektory
,
więc wektory
![]() są parami
ortogonalne. Niech
są parami
ortogonalne. Niech
Widzimy, że
![]() jest bazą ortonormalną
przestrzeni
jest bazą ortonormalną
przestrzeni ![]() .
.
Dla ![]() ,
, ![]() , więc
, więc
![]() jest bazą
ortonormalną przestrzeni
jest bazą
ortonormalną przestrzeni ![]() .
.
Przykład.
Niech
![]() będzie płaszczyzną o równaniu
będzie płaszczyzną o równaniu
![]() , gdzie
, gdzie
![\begin{displaymath}A=\left[\begin{array}{c}1 2 3\end{array}\right],\
B=\left[\begin{array}{c}3 2 1\end{array}\right].\end{displaymath}](img1470.png)
![\begin{displaymath}A'=\frac{1}{\sqrt{14}}A=\frac{1}{\sqrt{14}}\left[\begin{array}{c}1\\
2 3\end{array}\right].\end{displaymath}](img1473.png)
![\begin{displaymath}B^*=B-P_{A'}(B)=B-\langle B,A'\rangle
A'=\frac{4}{7}\left[\begin{array}{r}4 1 -2\end{array}\right].\end{displaymath}](img1474.png)
![\begin{displaymath}B'=\frac{1}{\Vert B^*\Vert}B^*=\frac{1}{\sqrt{21}}\left[\begin{array}{r}4\\
1 -2\end{array}\right]\end{displaymath}](img1477.png)
Zazwyczaj w przestrzeni euklidesowej jest wiele baz ortonormalnych.
Zastosowania.
1. Załóżmy, że ![]() jest podprzestrzenią przestrzeni euklidesowej
jest podprzestrzenią przestrzeni euklidesowej
![]() . Używając bazy ortonormalnej przestrzeni
. Używając bazy ortonormalnej przestrzeni ![]() możemy łatwo
zdefiniować rzut prostopadły
możemy łatwo
zdefiniować rzut prostopadły ![]() na przestrzeń
na przestrzeń ![]() . Przy pomocy
tego przekształcenia możemy określić odległość dowolnego
wektora
. Przy pomocy
tego przekształcenia możemy określić odległość dowolnego
wektora ![]() od podprzestrzeni
od podprzestrzeni ![]() wzorem
wzorem
W tym celu zauważmy, że
2. Definiujemy przekształcenie liniowe
![]() wzorem
wzorem
3. Załóżmy, że
![]() jest bazą ortonormalną
przestrzeni
jest bazą ortonormalną
przestrzeni ![]() . Przy użyciu tej bazy możemy łatwo obliczać
iloczyn skalarny
. Przy użyciu tej bazy możemy łatwo obliczać
iloczyn skalarny
![]() wektorów
wektorów ![]() .
.
Następna uwaga nie jest prawdziwa dla wszystkich przestrzeni euklidesowych. Tu dowodzimy jej dla przestrzeni skończonego wymiaru.
Zauważmy, że
Załóżmy teraz, że
![]() jest inną
przestrzenią euklidesową.
jest inną
przestrzenią euklidesową.
Odpowiednikiem twierdzenia 3.6 o izomorfizmie liniowym jest następujące twierdzenie o izomorfizmie przestrzeni euklidesowych.
Mozemy teraz podać głębsze uzasadnienie definicji odległości i
kąta między wektorami ![]() przestrzeni euklidesowej
przestrzeni euklidesowej
![]() . Mianowicie, rozważmy podprzestrzeń
. Mianowicie, rozważmy podprzestrzeń ![]() przestrzeni
przestrzeni
![]() . Przestrzeń
. Przestrzeń ![]() jest również przestrzenią euklidesową (z
iloczynem skalarnym pzestrzeni
jest również przestrzenią euklidesową (z
iloczynem skalarnym pzestrzeni ![]() ograniczonym do
ograniczonym do ![]() ). Dlatego na
mocy twierdzenia 11.4 istnieje izomorfizm liniowy
). Dlatego na
mocy twierdzenia 11.4 istnieje izomorfizm liniowy
![]() . Na płaszczyźnie euklidesowej
. Na płaszczyźnie euklidesowej ![]() mamy naturalne pojęcia
odległości i kąta między wektorami. łatwo sprawdzić, że
odległość i kąt między wektorami
mamy naturalne pojęcia
odległości i kąta między wektorami. łatwo sprawdzić, że
odległość i kąt między wektorami ![]() w przestrzeni
w przestrzeni ![]() równe
są odległości i kątowi między odpowiadającymi im wektorami
równe
są odległości i kątowi między odpowiadającymi im wektorami
![]() na płaszczyźnie
na płaszczyźnie ![]() .
.
Zwróćmy uwagę, że możemy jawnie zadać izomorfizm między
przestrzeniami ![]() we wniosku 11.6. Mianowicie, gdy
we wniosku 11.6. Mianowicie, gdy
![]() i
i
![]() są bazami
ortonormalnymi przestrzeni
są bazami
ortonormalnymi przestrzeni ![]() i
i ![]() odpowiednio, to przekształcenie
liniowe
odpowiednio, to przekształcenie
liniowe
![]() określone wzorem
określone wzorem
Osłabiając nieco warunki definicji izomorfizmu liniowego dostaliśmy w rozdziale 3 pojęcie przekształcenia liniowego. Podobnie, osłabiając nieco warunki definicji izomorfizmu przestrzeni euklidesowych dostajemy definicję izometrii liniowej.
Będziemy zajmować się przede wszystkim izometriami
![]() jednej przestrzeni euklidesowej skończonego wymiaru. W
większości dowody można łatwo uogólnić na przypadek dowolnych
izometrii liniowych. W następnym rozdziale opiszemy wszystkie
izometrie liniowe przestrzeni
jednej przestrzeni euklidesowej skończonego wymiaru. W
większości dowody można łatwo uogólnić na przypadek dowolnych
izometrii liniowych. W następnym rozdziale opiszemy wszystkie
izometrie liniowe przestrzeni ![]() .
.
Czytelnik zauważa zapewne, że termin ``izometria'' odnosić się
powinien do
zachowywania odległości, niekoniecznie zaś
do zachowywania również iloczynu skalarnego. Przykładowo,
translacja
![]() jest izometrią, bo zachowuje
odległości między wektorami. Zazwyczaj jednak
jest izometrią, bo zachowuje
odległości między wektorami. Zazwyczaj jednak ![]() nie spełnia
warunku
nie spełnia
warunku ![]() definicji 11.6. Następna uwaga pokazuje, że dla
przekształceń liniowych zachowywanie odległości jest równoważne
zachowywaniu iloczynu skalarnego.
definicji 11.6. Następna uwaga pokazuje, że dla
przekształceń liniowych zachowywanie odległości jest równoważne
zachowywaniu iloczynu skalarnego.
![]() . Zauważmy, że na mocy (2) i liniowości
. Zauważmy, że na mocy (2) i liniowości ![]() mamy
mamy
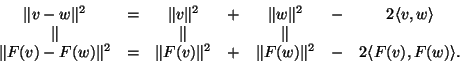
Dlatego
![]() .
.
Sprawdzenie, że ![]() jest również izometrią liniową
pozostawiamy jako ćwiczenie.
jest również izometrią liniową
pozostawiamy jako ćwiczenie.
Rozważymy teraz problem, jak rozpoznać w praktyce, czy
przekształcenie liniowe
![]() jest izometrią.
jest izometrią.
Następna uwaga daje proste kryterium do sprawdzania, czy dany endomorfizm jest izometrią liniową.
![]() .
.
![]() . Załóżmy, że
. Załóżmy, że
![]() jest ortogonalna.
Niech
jest ortogonalna.
Niech
![]() . Po pierwsze udowodnimy, że
. Po pierwsze udowodnimy, że
![]() jest bazą ortonormalną przestrzeni
jest bazą ortonormalną przestrzeni ![]() .
.
Pokażemy, że wektory ![]() mają długość
mają długość ![]() i są parami ortogonalne. Niech
i są parami ortogonalne. Niech
![]() .
.
Teraz pokażemy, że ![]() jest izometrią liniową. Niech
jest izometrią liniową. Niech
![]() . Wystarczy udowodnić, że
. Wystarczy udowodnić, że
![]() .
.
Zauważmy, że
![]() więc
więc
![]() i
i
![]() . Dlatego
. Dlatego
Bardzo łatwo obliczyć macierz odwrotną do macierzy ortogonalnej.
![]() Załóżmy, że
Załóżmy, że ![]() jest ortogonalna. Niech
jest ortogonalna. Niech
![]() będzie przekształceniem liniowym o macierzy
będzie przekształceniem liniowym o macierzy
![]() . Na mocy uwagi 11.11,
. Na mocy uwagi 11.11, ![]() jest izometrią liniową, więc jest
odwracalne (wniosek 11.9). Stąd wynika (uwaga 4.7), że macierz
jest izometrią liniową, więc jest
odwracalne (wniosek 11.9). Stąd wynika (uwaga 4.7), że macierz
![]() jest odwracalna. Pokażemy, że
jest odwracalna. Pokażemy, że ![]() . Zgodnie z definicją iloczynu macierzy,
. Zgodnie z definicją iloczynu macierzy,
![]() . Skoro macierz
. Skoro macierz ![]() jest ortogonalna,
to
jest ortogonalna,
to
![]() Załóżmy, że
Załóżmy, że ![]() . Znaczy to, że
. Znaczy to, że
![]() , więc
, więc
(2) Dowód przeprowadzimy dla ![]() . Załóżmy, że
. Załóżmy, że
![]() dla pewnego niezerowego wektora
dla pewnego niezerowego wektora ![]() . Wtedy na mocy uwag 10.3(0) i 11.8 mamy
. Wtedy na mocy uwag 10.3(0) i 11.8 mamy
Przykłady.
Niech
![]() będzie bazą ortonormalną przestrzeni
będzie bazą ortonormalną przestrzeni
![]() . Podamy 2 przykłady izometrii liniowych przestrzeni
. Podamy 2 przykłady izometrii liniowych przestrzeni ![]() .
.
1. Niech
![]() .
. ![]() jest podprzestrzenią wymiaru
jest podprzestrzenią wymiaru
![]() , takie podprzestrzenie nazywamy
płaszczyznami.
, takie podprzestrzenie nazywamy
płaszczyznami.
![]() i
i
![]() . Stosując izomorfizm z twierdzenia 11.5, możemy
myśleć o przestrzeni
. Stosując izomorfizm z twierdzenia 11.5, możemy
myśleć o przestrzeni ![]() jak o standardowej przestrzeni
jak o standardowej przestrzeni ![]() ,
zaś o wektorach
,
zaś o wektorach ![]() jak o wektorach
jak o wektorach
![]() . Niech
. Niech
![]() . Obrotem przestrzeni
. Obrotem przestrzeni ![]() w
płaszczyźnie
w
płaszczyźnie ![]() (wokół przestrzeni
(wokół przestrzeni ![]() ) nazywamy
przekształcenie liniowe
) nazywamy
przekształcenie liniowe
![]() o macierzy
o macierzy
![\begin{displaymath}m_{{\cal B}}(R^{\alpha}_W)=\left[\begin{array}{rrccc}\cos(\al...
...ddots&\mbox{}\\
0&\mbox{}&\mbox{}&\mbox{}&1\end{array}\right].\end{displaymath}](img1569.png)
2. Innym przykładem izometrii liniowej jest odbicie przestrzeni ![]() względem jej podprzestrzeni (określone przed uwagą
11.2). Zbadamy dokładniej odbicie względem
hiperpłaszczyzny. Mianowicie niech
względem jej podprzestrzeni (określone przed uwagą
11.2). Zbadamy dokładniej odbicie względem
hiperpłaszczyzny. Mianowicie niech
![]() . Podprzestrzeń
. Podprzestrzeń ![]() ma wymiar
ma wymiar ![]() . Podprzestrzenie
takie nazywamy hiperpłaszczyznami.
. Podprzestrzenie
takie nazywamy hiperpłaszczyznami.
![]() . Odbicie
. Odbicie
![]() względem hiperpłaszczyzny
względem hiperpłaszczyzny ![]() ma macierz
ma macierz
![\begin{displaymath}m_{{\cal B}}(S_U)=\left[\begin{array}{rccc}-1&\mbox{}&\mbox{}...
...mbox{}&\ddots&\mbox{}\\
0&\mbox{}&\mbox{}&1\end{array}\right].\end{displaymath}](img1577.png)