W tym rozdziale zbadamy układy równań liniowych, stosując do tego
wprowadzone już pojęcia algebry liniowej. Rozważmy następujący
układ ![]() równań liniowych z
równań liniowych z ![]() niewiadomymi
niewiadomymi ![]() .
.
![\begin{displaymath}\mbox{[U]}\left\{\begin{array}{ccccccccc}
a_{11}x_1&+&a_{12}x...
...r1}x_1&+&a_{r2}x_2&+&\cdots&+&a_{rn}x_n&=&b_r\end{array}\right.\end{displaymath}](img1227.png)
1. Czy układ [U] ma rozwiązanie w zbiorze liczb rzeczywistych ![]() ?
?
2. Jak opisać zbiór rozwiązań [U] ?
3. Jak praktycznie rozwiązać układ [U] ?
Gdy
![]() , mówimy, że układ [U] jest
jednorodny. Oznaczmy przez [UJ] układ równań powstały z układu
[U] przez zastąpienie parametrów
, mówimy, że układ [U] jest
jednorodny. Oznaczmy przez [UJ] układ równań powstały z układu
[U] przez zastąpienie parametrów ![]() zerami. [UJ]
nazywamy jednorodnym układem równań związanym z [U].
zerami. [UJ]
nazywamy jednorodnym układem równań związanym z [U].
Parametry ![]() układu [U] tworzą macierz
układu [U] tworzą macierz
![]() zwaną macierzą główną układu [U] (i układu [UJ]). Kolejne
kolumny macierzy
zwaną macierzą główną układu [U] (i układu [UJ]). Kolejne
kolumny macierzy ![]() odpowiadają kolejnym niewiadomym
odpowiadają kolejnym niewiadomym ![]() . Gdy do
macierzy
. Gdy do
macierzy ![]() dopiszemy jako ostatnią kolumnę parametry
dopiszemy jako ostatnią kolumnę parametry
![]() , dostaniemy macierz
, dostaniemy macierz ![]() wymiaru
wymiaru ![]() ,
zwaną macierzą rozszerzoną układu [U].
,
zwaną macierzą rozszerzoną układu [U].
Macierz ![]() wyznacza przekształcenie liniowe
wyznacza przekształcenie liniowe
![]() dane wzorem
dane wzorem
![]() . Traktując zmienne
. Traktując zmienne ![]() jako
współrzędne wektora
jako
współrzędne wektora
![]() , możemy zapisać układ równań
[U] w następujących równoważnych postaciach.
, możemy zapisać układ równań
[U] w następujących równoważnych postaciach.
![\begin{displaymath}X=\left[\begin{array}{c}x_1\\
\vdots x_n\end{array}\right], B=\left[\begin{array}{c}b_1 \vdots b_r\end{array}\right].\end{displaymath}](img1238.png)
Oznaczmy przez ![]() zbiór rozwiązań układu [U], zaś przez
zbiór rozwiązań układu [U], zaś przez ![]() zbiór rozwiązań układu [UJ].
Zbiory te traktujemy jak podzbiory
przestrzeni
zbiór rozwiązań układu [UJ].
Zbiory te traktujemy jak podzbiory
przestrzeni
![]() .
.
2) Układ [U] ma rozwiązanie
![]()
![]() dla pewnego
dla pewnego
![]() .
Załóżmy, że
.
Załóżmy, że ![]() jest pewnym rozwiązaniem [U], to znaczy
jest pewnym rozwiązaniem [U], to znaczy ![]() . Pokażemy, że
. Pokażemy, że
![]() jest warstwą
jest warstwą ![]() . Dla
. Dla
![]() mamy
mamy
Przy pomocy następnego twierdzenia możemy łatwo rozstrzygnąć, czy układ [U] ma rozwiązanie.
Załóżmy, że układ [U] ma rozwiązanie (tzn. jest niesprzeczny).
Na mocy faktu 9.1,
![]() , gdzie
, gdzie ![]() jest dowolnym
rozwiązaniem [U]. Niech
jest dowolnym
rozwiązaniem [U]. Niech ![]() będzie bazą przestrzeni
będzie bazą przestrzeni
![]() . Wówczas zbiór rozwiązań
. Wówczas zbiór rozwiązań ![]() możemy opisać równaniem w
postaci parametrycznej
możemy opisać równaniem w
postaci parametrycznej
Do rozwiązywania układu równań [U] w praktyce służy metoda
eliminacji niewiadomych, zwana też metodą Gaussa.
By opisać tę metodę, zauważmy, że następujące operacje na
równaniach układu [U] nie zmieniają zbioru rozwiązań ![]() :
:
Operacje te wygodnie jest przeprowadzać nie bezpośrednio na
układzie [U], lecz na jego macierzy rozszerzonej ![]() . Wówczas
odpowiadają one operacjom (1),(2),(3) z faktu 7.7.
. Wówczas
odpowiadają one operacjom (1),(2),(3) z faktu 7.7.
Metoda Gaussa polega na takim przekształceniu macierzy rozszerzonej ![]() układu [U] poprzez operacje z faktu 7.7, by otrzymać macierz
układu [U] poprzez operacje z faktu 7.7, by otrzymać macierz ![]() (wymiaru
(wymiaru ![]() )
z uporządkowanymi wierszami. Macierz ta odpowiada pewnemu układowi
równań [U'] równoważnemu układowi [U]. Jeśli teraz w macierzy
)
z uporządkowanymi wierszami. Macierz ta odpowiada pewnemu układowi
równań [U'] równoważnemu układowi [U]. Jeśli teraz w macierzy
![]() wyraz wiodący w pewnym wierszu znajduje się w ostatniej
kolumnie, to układ równań [U] jest sprzeczny (nie ma
rozwiązań). W przeciwnym razie układ [U] jest niesprzeczny i
możemy znaleźć jego rozwiązania w następujący sposób.
wyraz wiodący w pewnym wierszu znajduje się w ostatniej
kolumnie, to układ równań [U] jest sprzeczny (nie ma
rozwiązań). W przeciwnym razie układ [U] jest niesprzeczny i
możemy znaleźć jego rozwiązania w następujący sposób.
Zmienne ![]() odpowiadające kolumnom macierzy
odpowiadające kolumnom macierzy ![]() zawierającym
wyraz wiodący w jakimś wierszu nazywamy zmiennymi związanymi,
pozostałe zmienne nazywamy zmiennymi parametrycznymi. Przekształcamy
układ [U'] wyrażając zmienne związane przy pomocy parametrów
układu [U'] i zmiennych parametrycznych, dostając w ten sposób
parametryczne rozwiązanie układu [U]. Prześledzimy teraz tę
metodę na przykładzie.
zawierającym
wyraz wiodący w jakimś wierszu nazywamy zmiennymi związanymi,
pozostałe zmienne nazywamy zmiennymi parametrycznymi. Przekształcamy
układ [U'] wyrażając zmienne związane przy pomocy parametrów
układu [U'] i zmiennych parametrycznych, dostając w ten sposób
parametryczne rozwiązanie układu [U]. Prześledzimy teraz tę
metodę na przykładzie.
Przykład. Rozważmy układ
![\begin{displaymath}\mbox{[U]}\left\{\begin{array}{ccccccccc}
-x_1&+&3x_2&+&2x_3&...
...3\\
x_1&+&\mbox{}&\mbox{}&x_3&+&4x_4&=&3\\
\end{array}\right.\end{displaymath}](img1264.png)
![\begin{displaymath}\left[\begin{array}{rrrrr}-1&3&2&-1&0\\
1&-2&-1&2&1\\
2&-3&...
...!\!\begin{array}{l}\mbox{} \mbox{} -3[2] -3[2]\end{array}\end{displaymath}](img1265.png)
![\begin{displaymath}\longrightarrow\left[\begin{array}{rrrrr}-1&3&2&-1&0 0&1&1&1&1\\
0&0&0&0&0 0&0&0&0&0\end{array}\right]\end{displaymath}](img1266.png)
![\begin{displaymath}X_0=\left[\begin{array}{c}3 1 0\\
0\end{array}\right].\end{displaymath}](img1275.png)
![\begin{displaymath}X=\left[\begin{array}{c}3-x_3-4x_4 1-x_3-x_4 x_3\\
x_4\e...
...{r}-4 -1 0 1\end{array}\right], x_3,x_4\in {\mathbb{R}}.\end{displaymath}](img1276.png)
![\begin{displaymath}X_1=\left[\begin{array}{r}-1 -1 1\\
0\end{array}\right], X_2=\left[\begin{array}{r}-4 -1 0\\
1\end{array}\right]\end{displaymath}](img1277.png)
![\begin{displaymath}X=\left[\begin{array}{c}-x_3-4x_4 -x_3-x_4 x_3\\
x_4\end{array}\right], x_3,x_4\in {\mathbb{R}}.\end{displaymath}](img1278.png)
![\begin{displaymath}F\left[\begin{array}{cc}x_3 x_4\end{array}\right]=\left[\begin{array}{c}-x_3-4x_4 -x_3-x_4 x_3\\
x_4\end{array}\right].\end{displaymath}](img1280.png)
Jeślibyśmy w 3 równaniu
układu [U] zmienili liczbe ![]() po prawej stronie równości na
liczbę
po prawej stronie równości na
liczbę ![]() , to stosując powyższe operacje doprowadzilibyśmy
macierz rozszerzoną układu [U] do postaci z uporządkowanymi
wierszami, gdzie wyraz wiodący w 3 wierszu znajdowałby sie w
ostatniej kolumnie. Byłby to więc układ sprzeczny.
, to stosując powyższe operacje doprowadzilibyśmy
macierz rozszerzoną układu [U] do postaci z uporządkowanymi
wierszami, gdzie wyraz wiodący w 3 wierszu znajdowałby sie w
ostatniej kolumnie. Byłby to więc układ sprzeczny.
Rozważymy teraz szczególny przypadek układu ![]() równań liniowych
z
równań liniowych
z ![]() niewiadomymi (stosujemy zapis macierzowy)
niewiadomymi (stosujemy zapis macierzowy)
Możemy teraz uzasadnić ``bezwyznacznikową metodę'' obliczania
macierzy odwrotnej ![]() opisaną w rozdziale 6. Rozważmy
mianowicie układ równości
opisaną w rozdziale 6. Rozważmy
mianowicie układ równości
![]() , gdzie
, gdzie
![]() .
Możemy go zapisać w postaci
.
Możemy go zapisać w postaci
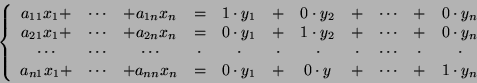
Powróćmy do układu równań ![]() . Zapiszmy macierz
. Zapiszmy macierz ![]() w postaci
ciągu kolumn
w postaci
ciągu kolumn
![]() . Przez
. Przez ![]() oznaczamy macierz
powstałą przez zastąpienie w macierzy
oznaczamy macierz
powstałą przez zastąpienie w macierzy ![]()
![]() -tej kolumny przez
-tej kolumny przez
![]() .
Następujące twierdzenie pokazuje kolejne zastosowanie wyznacznika.
.
Następujące twierdzenie pokazuje kolejne zastosowanie wyznacznika.
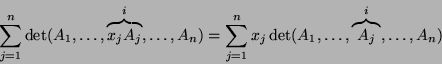
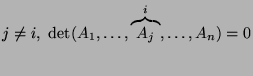 ,
podczas gdy dla
,
podczas gdy dla 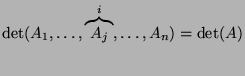 .
Stąd natychmiast dostajemy, że
.
Stąd natychmiast dostajemy, że